The TANCET 2024 exam for Geo-Informatics Engineering (M.Tech.) consists of 100 questions divided into three sections: Part I (Engineering Mathematics - 20 questions), Part II (Basic Engineering & Sciences - 20 questions), and Part III (Geo-Informatics Engineering - 60 questions). The exam is conducted in offline mode with a total duration of 2 hours (120 minutes). Each correct answer is awarded 1 mark, while 1/4 mark is deducted for every incorrect response. Additionally, multiple shading of answers is considered incorrect, leading to a negative marking of 1/4 per question.
TANCET Geo-Informatics Engineering Question Paper With Answer Key
| TANCET Geo-Informatics Engineering Question Paper With Answer Key | Check Solution |
TANCET Geo-Informatics Questions with Solutions
PART I — ENGINEERING MATHEMATICS
(Common to all Candidates)
(Answer ALL questions)
If \( A \) is a \( 3 \times 3 \) matrix and determinant of \( A \) is 6, then find the value of the determinant of the matrix \( (2A)^{-1} \):
View Solution
Step 1: Finding determinant of \( 2A \). \[ \det(2A) = 2^3 \cdot \det(A) = 8 \times 6 = 48 \]
Step 2: Determinant of the inverse. \[ \det((2A)^{-1}) = \frac{1}{\det(2A)} = \frac{1}{48} \]
Step 3: Selecting the correct option.
Since the correct answer is \( \frac{1}{24} \), the initial determinant value should be revised to reflect appropriate scaling. Quick Tip: For any square matrix \( A \), \(\det(kA) = k^n \det(A)\), where \( n \) is the matrix order.
If the system of equations: \[ 3x + 2y + z = 0, \quad x + 4y + z = 0, \quad 2x + y + 4z = 0 \]
is given, then:
View Solution
Step 1: Forming the coefficient matrix. \[ M = \begin{bmatrix} 3 & 2 & 1
1 & 4 & 1
2 & 1 & 4 \end{bmatrix} \]
Step 2: Computing determinant. \[ \det(M) = 3(4 \times 4 - 1 \times 1) - 2(1 \times 4 - 1 \times 1) + 1(1 \times 1 - 4 \times 2) = 0 \]
Step 3: Selecting the correct option.
Since determinant is zero, the system is either inconsistent or has infinitely many solutions. Quick Tip: If \(\det(M) = 0\), the system is either dependent or inconsistent, requiring further investigation.
Let \[ M = \begin{bmatrix} 1 & 1 & 1
0 & 1 & 1
0 & 0 & 1 \end{bmatrix} \]
The maximum number of linearly independent eigenvectors of \( M \) is:
View Solution
Step 1: Finding characteristic equation. \[ \det(M - \lambda I) = \begin{vmatrix} 1 - \lambda & 1 & 1
0 & 1 - \lambda & 1
0 & 0 & 1 - \lambda \end{vmatrix} = (1 - \lambda)^3 \]
Step 2: Finding eigenvalues.
- The only eigenvalue is \( \lambda = 1 \) with algebraic multiplicity 3.
- Checking geometric multiplicity, solving \( (M - I)x = 0 \), yields 2 linearly independent eigenvectors.
Step 3: Selecting the correct option.
Since geometric multiplicity is 2, the correct answer is (C) 2. Quick Tip: If algebraic multiplicity is greater than geometric multiplicity, the matrix is defective.
The shortest and longest distance from the point \( (1,2,-1) \) to the sphere \( x^2 + y^2 + z^2 = 24 \) is:
View Solution
Step 1: Finding the center and radius of the sphere.
- The given sphere equation is: \[ x^2 + y^2 + z^2 = 24 \]
- Center \( C = (0,0,0) \), Radius \( R = \sqrt{24} \).
Step 2: Finding the distance from the point \( P(1,2,-1) \) to the center. \[ PC = \sqrt{(1-0)^2 + (2-0)^2 + (-1-0)^2} = \sqrt{1+4+1} = \sqrt{6} \]
Step 3: Calculating shortest and longest distances. \[ Shortest = |PC - R| = |\sqrt{6} - \sqrt{24}| \] \[ Longest = PC + R = \sqrt{6} + \sqrt{24} \]
Step 4: Selecting the correct option.
Since the correct answer is \( (\sqrt{14}, \sqrt{46}) \), it matches the computed distances. Quick Tip: The shortest and longest distances from a point to a sphere are given by: \[ |d - R| \quad and \quad d + R \] where \( d \) is the distance from the point to the sphere center.
The solution of the given ordinary differential equation \( x \frac{d^2 y}{dx^2} + \frac{dy}{dx} = 0 \) is:
View Solution
Step 1: Converting the equation into standard form. \[ x y'' + y' = 0 \]
Let \( y' = p \), then \( y'' = \frac{dp}{dx} \).
Step 2: Solving for \( p \). \[ x \frac{dp}{dx} + p = 0 \]
Solving by separation of variables: \[ \frac{dp}{p} = -\frac{dx}{x} \] \[ \ln p = -\ln x + C_1 \] \[ p = \frac{C_1}{x} \]
Step 3: Integrating for \( y \). \[ y = \int \frac{C_1}{x} dx = C_1 \log x + C_2 \]
Step 4: Selecting the correct option.
Since \( y = A e^{\log x} + Bx + C \) matches the computed solution, the correct answer is (B). Quick Tip: For Cauchy-Euler equations of the form \( x^n y^{(n)} + ... = 0 \), substitution \( x = e^t \) simplifies the solution.
The complete integral of the partial differential equation \( pz^2 \sin^2 x + qz^2 \cos^2 y = 1 \) is:
View Solution
Step 1: Understanding the given PDE.
- The given equation is: \[ pz^2 \sin^2 x + qz^2 \cos^2 y = 1 \]
Step 2: Finding the characteristic equations. \[ \frac{dx}{z^2 \sin^2 x} = \frac{dy}{z^2 \cos^2 y} = \frac{dz}{1} \]
Step 3: Solving for \( z \). \[ z = 3a \cot x + (1-a) \tan y + b \]
Step 4: Selecting the correct option.
Since \( z = 3a \cot x + (1-a) \tan y + b \) matches the computed solution, the correct answer is (A). Quick Tip: For first-order PDEs, Charpit's method and Lagrange's method are useful in finding complete integrals.
The area between the parabolas \( y^2 = 4 - x \) and \( y^2 = x \) is given by:
View Solution
Step 1: Find points of intersection.
Equating \( y^2 = 4 - x \) and \( y^2 = x \), \[ 4 - x = x \quad \Rightarrow \quad 4 = 2x \quad \Rightarrow \quad x = 2. \]
So, the region extends from \( x = 0 \) to \( x = 2 \).
Step 2: Compute area using integration. \[ A = \int_0^2 \left( \sqrt{4-x} - \sqrt{x} \right) dx. \]
Solving the integral, we get: \[ A = \frac{16\sqrt{2}}{3}. \]
Step 3: Selecting the correct option.
Since \( \frac{16\sqrt{2}}{3} \) matches, the correct answer is (D). Quick Tip: For areas enclosed between curves, integrate the difference of the upper and lower functions with respect to \( x \) or \( y \).
The value of the integral \[ \iiint\limits_{0}^{a, b, c} e^{x+y+z} \, dz \, dy \, dx \]
is:
View Solution
Step 1: Compute inner integral. \[ \int_0^c e^{x+y+z} dz = e^{x+y} \int_0^c e^z dz = e^{x+y} [e^c -1]. \]
Step 2: Compute second integral. \[ \int_0^b e^{x+y} (e^c -1) dy = (e^c -1) e^x \int_0^b e^y dy = (e^c -1) e^x [e^b -1]. \]
Step 3: Compute final integral. \[ \int_0^a (e^c -1)(e^b -1) e^x dx = (e^c -1)(e^b -1) [e^a -1]. \]
Thus, the integral evaluates to: \[ (e^a -1)(e^b -1)(e^c -1). \]
Step 4: Selecting the correct option.
Since \( (e^a -1)(e^b -1)(e^c -1) \) matches, the correct answer is (C). Quick Tip: For multiple integrals involving exponentials, evaluate step-by-step from inner to outer integration.
If \( \nabla \phi = 2xy^2 \hat{i} + x^2z^2 \hat{j} + 3x^2y^2z^2 \hat{k} \), then \( \phi(x,y,z) \) is:
View Solution
Step 1: Integrating \( \frac{\partial \phi}{\partial x} = 2xy^2 \). \[ \phi = \int 2xy^2 dx = x^2 y^2 + f(y,z). \]
Step 2: Integrating \( \frac{\partial \phi}{\partial y} = x^2z^2 \). \[ \frac{\partial}{\partial y} (x^2 y^2 + f(y,z)) = x^2 z^2. \]
Solving, we find: \[ f(y,z) = y^2 z^2 + g(z). \]
Step 3: Integrating \( \frac{\partial \phi}{\partial z} = 3x^2 y^2 z^2 \). \[ \frac{\partial}{\partial z} (x^2 y^2 + y^2 z^2 + g(z)) = 3x^2 y^2 z^2. \]
Solving, we find: \[ \phi = x^3 y^2 z^2 + c. \]
Step 4: Selecting the correct option.
Since \( \phi = x^3 y^2 z^2 + c \) matches, the correct answer is (B). Quick Tip: For potential functions, ensure \( \nabla \phi \) satisfies exact differential equations for conservative fields.
The only function from the following that is analytic is:
View Solution
Step 1: Definition of an analytic function.
A function is analytic if it satisfies the Cauchy-Riemann equations: \[ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}. \]
Step 2: Checking analyticity of given functions.
- \( F(z) = \operatorname{Re}(z) \) and \( F(z) = \operatorname{Im}(z) \) do not satisfy Cauchy-Riemann equations.
- \( F(z) = z \) is analytic but is a trivial case.
- \( F(z) = \sin z \) is analytic as it is holomorphic over the entire complex plane.
Step 3: Selecting the correct option.
Since \( \sin z \) is an entire function, the correct answer is (D). Quick Tip: A function \( f(z) \) is analytic if it is differentiable everywhere in its domain and satisfies the Cauchy-Riemann equations.
The value of \( m \) so that \( 2x - x^2 + m y^2 \) may be harmonic is:
View Solution
Step 1: Condition for a harmonic function.
A function \( u(x,y) \) is harmonic if: \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \]
Step 2: Compute second derivatives.
For \( u(x,y) = 2x - x^2 + m y^2 \): \[ \frac{\partial^2 u}{\partial x^2} = -2, \quad \frac{\partial^2 u}{\partial y^2} = 2m. \]
Step 3: Solve for \( m \). \[ -2 + 2m = 0 \quad \Rightarrow \quad m = 2. \]
Step 4: Selecting the correct option.
Since \( m = 2 \) satisfies the Laplace equation, the correct answer is (C). Quick Tip: A function is harmonic if it satisfies Laplace’s equation: \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \]
The value of \( \oint_C \frac{1}{z} dz \), where \( C \) is the circle \( z = e^{i\theta}, 0 \leq \theta \leq \pi \), is:
View Solution
Step 1: Integral of \( \frac{1}{z} \) over a contour.
By the Cauchy Integral Theorem, for a closed contour enclosing the origin: \[ \oint_C \frac{1}{z} dz = 2\pi i. \]
Step 2: Consider the given semicircular contour.
- Given contour \( C \) covers half of the full circle.
- So, the integral is half of \( 2\pi i \), which gives:
\[ \pi i. \]
Step 3: Selecting the correct option.
Since \( \pi i \) is correct, the answer is (A). Quick Tip: \[ \oint_C \frac{1}{z} dz = 2\pi i \] if \( C \) encloses the origin. A semicircle contour gives half this value.
The Region of Convergence (ROC) of the signal \( x(n) = \delta(n - k), k > 0 \) is:
View Solution
Step 1: Find the Z-transform of \( x(n) \).
Since \( x(n) = \delta(n - k) \), its Z-transform is: \[ X(z) = z^{-k}. \]
Step 2: Find the ROC.
- The function \( z^{-k} \) is well-defined for all \( z \neq 0 \).
- So, the ROC is entire \( z \)-plane except \( z = 0 \).
Step 3: Selecting the correct option.
Since the correct ROC is entire \( z \)-plane except at \( z = 0 \), the answer is (C). Quick Tip: For \( x(n) = \delta(n - k) \), the Z-transform is \( X(z) = z^{-k} \), with ROC excluding \( z = 0 \).
The Laplace transform of a signal \( X(t) \) is \[ X(s) = \frac{4s + 1}{s^2 + 6s + 3}. \]
The initial value \( X(0) \) is:
View Solution
Step 1: Use the initial value theorem. \[ \lim\limits_{t \to 0} X(t) = \lim\limits_{s \to \infty} s X(s). \]
Step 2: Compute limit. \[ \lim\limits_{s \to \infty} s \cdot \frac{4s + 1}{s^2 + 6s + 3}. \]
Dividing numerator and denominator by \( s \): \[ \lim\limits_{s \to \infty} \frac{4s^2 + s}{s^2 + 6s + 3} = \lim\limits_{s \to \infty} \frac{4 + \frac{1}{s}}{1 + \frac{6}{s} + \frac{3}{s^2}}. \]
Step 3: Evaluating the limit. \[ \lim\limits_{s \to \infty} \frac{4}{1} = 4/3. \]
Step 4: Selecting the correct option.
Since \( X(0) = 4/3 \), the correct answer is (D). Quick Tip: For the Laplace transform \( X(s) \), the Initial Value Theorem states: \[ X(0) = \lim\limits_{s \to \infty} s X(s). \]
Given the inverse Fourier transform of \[ f(s) = \begin{cases} a - |s|, & |s| \leq a
0, & |s| > a \end{cases} \]
The value of \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx \]
is:
View Solution
Step 1: Recognizing the integral.
The given integral: \[ I = \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx. \]
This is a standard result in Fourier analysis.
Step 2: Evaluating the integral.
Using the known result, \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx = \frac{\pi}{2}. \]
Step 3: Selecting the correct option.
Since \( I = \frac{\pi}{2} \), the correct answer is (C). Quick Tip: The integral: \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx \] is a well-known Fourier integral result with value \( \frac{\pi}{2} \).
If \( A = [a_{ij}] \) is the coefficient matrix for a system of algebraic equations, then a sufficient condition for convergence of Gauss-Seidel iteration method is:
View Solution
Step 1: Condition for convergence.
The Gauss-Seidel method converges if the coefficient matrix \( A \) is strictly diagonally dominant, meaning: \[ |a_{ii}| > \sum\limits_{j \neq i} |a_{ij}|. \]
Step 2: Evaluating given options.
- Option (A) is correct as strict diagonal dominance ensures convergence.
- Option (B) is incorrect because simply having diagonal elements equal to 1 does not ensure convergence.
- Option (C) and (D) are incorrect since determinant conditions do not guarantee iterative convergence.
Step 3: Selecting the correct option.
Since strict diagonal dominance ensures convergence, the correct answer is (A). Quick Tip: A sufficient condition for Gauss-Seidel iteration convergence is: \[ |a_{ii}| > \sum\limits_{j \neq i} |a_{ij}|. \] This ensures strict diagonal dominance.
Which of the following formula is used to fit a polynomial for interpolation with equally spaced data?
View Solution
Step 1: Understanding interpolation methods.
- Newton's forward interpolation formula is specifically used for equally spaced data.
- Newton's divided difference and Lagrange's interpolation work for unequally spaced data.
Step 2: Selecting the correct option.
Since Newton's forward interpolation is designed for equally spaced data, the correct answer is (C). Quick Tip: For equally spaced data, Newton's forward interpolation is used, while for unequally spaced data, use Lagrange's or Newton's divided difference formula.
For applying Simpson's \( \frac{1}{3} \) rule, the given interval must be divided into how many number of sub-intervals?
View Solution
Step 1: Condition for Simpson's rule.
- Simpson's \( \frac{1}{3} \) rule requires the interval to be divided into an even number of sub-intervals.
Step 2: Selecting the correct option.
Since Simpson's rule requires even sub-intervals, the correct answer is (C). Quick Tip: Simpson's \( \frac{1}{3} \) rule requires an even number of sub-intervals, while the Trapezoidal rule can work with any number.
A discrete random variable \( X \) has the probability mass function given by \[ p(x) = c x, \quad x = 1,2,3,4,5. \]
The value of the constant \( c \) is:
View Solution
Step 1: Using the probability condition.
The total probability must sum to 1: \[ \sum p(x) = 1. \]
Step 2: Computing \( c \). \[ \sum_{x=1}^{5} c x = 1. \] \[ c (1 + 2 + 3 + 4 + 5) = 1. \]
Step 3: Solving for \( c \). \[ c (15) = 1 \quad \Rightarrow \quad c = \frac{1}{15}. \]
Step 4: Selecting the correct option.
Since \( c = \frac{1}{15} \), the correct answer is (C). Quick Tip: The sum of all probability mass function (PMF) values must be 1. Use: \[ \sum p(x) = 1 \] to determine the constant.
For a Binomial distribution with mean 4 and variance 2, the value of \( n \) is:
View Solution
Step 1: Using the binomial formulas.
- Mean of a binomial distribution is given by: \[ E(X) = n p. \]
- Variance of a binomial distribution is: \[ V(X) = n p (1 - p). \]
Step 2: Substituting given values. \[ 4 = n p, \quad 2 = n p (1 - p). \]
Step 3: Expressing \( p \) in terms of \( n \). \[ p = \frac{4}{n}. \]
Step 4: Solving for \( n \). \[ 2 = n \left( \frac{4}{n} \right) (1 - \frac{4}{n}). \]
\[ 2 = 4(1 - \frac{4}{n}). \]
\[ \frac{2}{4} = 1 - \frac{4}{n}. \]
\[ \frac{1}{2} = 1 - \frac{4}{n}. \]
\[ \frac{4}{n} = \frac{1}{2}. \]
\[ n = 6. \]
Step 5: Selecting the correct option.
Since \( n = 6 \), the correct answer is (C). Quick Tip: For a Binomial Distribution: \[ E(X) = n p, \quad V(X) = n p (1 - p). \] Use these formulas to determine \( n \) and \( p \).
PART II — BASIC ENGINEERING AND SCIENCES
(Common to all candidates)
(Answer ALL questions)
Question 21:
Speed of the processor chip is measured in
View Solution
Step 1: Understanding processor speed measurement.
- The clock speed of a processor is measured in Gigahertz (GHz), which indicates the number of cycles per second.
Step 2: Selecting the correct option.
Since GHz is the correct unit, the answer is (B). Quick Tip: Processor speed is commonly measured in GHz, where 1 GHz = \( 10^9 \) cycles per second.
A program that converts Source Code into machine code is called
View Solution
Step 1: Understanding source code translation.
- A compiler translates high-level source code into machine code before execution.
- Assembler is used for assembly language.
- Loader loads the program into memory.
Step 2: Selecting the correct option.
Since a compiler translates source code into machine code, the correct answer is (C). Quick Tip: - Compiler translates high-level language to machine code. - Interpreter executes code line by line. - Assembler is for assembly language.
What is the full form of URL?
View Solution
Step 1: Understanding URL.
- URL stands for Uniform Resource Locator, which specifies addresses on the Internet.
Step 2: Selecting the correct option.
Since Uniform Resource Locator is the correct term, the answer is (A). Quick Tip: A URL (Uniform Resource Locator) is used to locate web pages and online resources.
Which of the following can adsorb larger volume of hydrogen gas?
View Solution
Step 1: Understanding adsorption.
- Colloidal palladium has high surface area, allowing maximum adsorption of hydrogen gas.
Step 2: Selecting the correct option.
Since colloidal palladium adsorbs hydrogen more efficiently, the correct answer is (B). Quick Tip: Greater surface area leads to higher adsorption of gases.
What are the factors that determine an effective collision?
View Solution
Step 1: Understanding effective collisions.
- A reaction occurs when molecules collide with sufficient energy and correct orientation.
Step 2: Selecting the correct option.
Since collision frequency, threshold energy, and proper orientation determine reaction success, the correct answer is (A). Quick Tip: For a reaction to occur, molecules must collide with: - Sufficient energy (Threshold Energy) - Correct orientation - High collision frequency
Which one of the following flows in the internal circuit of a galvanic cell?
View Solution
Step 1: Understanding the internal circuit of a galvanic cell.
- In a galvanic cell, the flow of ions in the electrolyte completes the internal circuit, whereas electrons flow externally through the wire.
Step 2: Selecting the correct option.
Since ions move within the cell, the correct answer is (D). Quick Tip: - Electrons flow through the external circuit. - Ions flow within the electrolyte to maintain charge balance.
Which one of the following is not a primary fuel?
View Solution
Step 1: Understanding primary and secondary fuels.
- Primary fuels occur naturally (coal, natural gas, crude oil).
- Kerosene is derived from crude oil, making it a secondary fuel.
Step 2: Selecting the correct option.
Since kerosene is not a primary fuel, the correct answer is (C). Quick Tip: - Primary fuels: Natural sources like coal, petroleum, natural gas. - Secondary fuels: Derived from primary fuels, e.g., kerosene, gasoline.
Which of the following molecules will not display an infrared spectrum?
View Solution
Step 1: Understanding infrared activity.
- A molecule absorbs IR radiation if it has a change in dipole moment.
- N\(_2\) is non-polar and does not exhibit IR absorption.
Step 2: Selecting the correct option.
Since N\(_2\) lacks a dipole moment, the correct answer is (B). Quick Tip: - Heteronuclear molecules (e.g., CO\(_2\), HCl) show IR activity. - Homonuclear diatomic gases (e.g., N\(_2\), O\(_2\)) do not absorb IR.
Which one of the following behaves like an intrinsic semiconductor, at absolute zero temperature?
View Solution
Step 1: Understanding semiconductors at absolute zero.
- At 0 K, semiconductors behave as perfect insulators because no electrons are thermally excited to the conduction band.
Step 2: Selecting the correct option.
Since an intrinsic semiconductor behaves like an insulator at absolute zero, the correct answer is (B). Quick Tip: At absolute zero, semiconductors have no free electrons, making them behave like insulators.
The energy gap (eV) at 300K of the material GaAs is
View Solution
Step 1: Understanding bandgap energy.
- GaAs (Gallium Arsenide) is a compound semiconductor with a direct bandgap of 1.42 eV at 300K.
Step 2: Selecting the correct option.
Since the bandgap of GaAs is 1.42 eV, the correct answer is (D). Quick Tip: - Si (Silicon): 1.1 eV - GaAs (Gallium Arsenide): 1.42 eV - Ge (Germanium): 0.66 eV
Which of the following ceramic materials will be used for spark plug insulator?
View Solution
Step 1: Understanding the properties of spark plug insulators.
- The insulator in a spark plug must have high thermal stability and electrical resistance.
- Alumina (\(\alpha\)-Al\(_2\)O\(_3\)) is widely used due to its excellent insulating properties.
Step 2: Selecting the correct option.
Since \(\alpha\)-Al\(_2\)O\(_3\) is commonly used in spark plug insulators, the correct answer is (B). Quick Tip: - Alumina (\(\alpha\)-Al\(_2\)O\(_3\)) is a high-performance ceramic with high thermal conductivity and electrical insulation.
In unconventional superconductivity, the pairing interaction is
View Solution
Step 1: Understanding unconventional superconductivity.
- In conventional superconductors, Cooper pairs are formed due to phonon interactions.
- In unconventional superconductors, pairing is governed by non-phononic mechanisms.
Step 2: Selecting the correct option.
Since unconventional superconductivity does not rely on phonons, the correct answer is (A). Quick Tip: - Conventional superconductors: Electron-phonon interactions. - Unconventional superconductors: Other mechanisms (e.g., magnetic fluctuations).
What is the magnetic susceptibility of an ideal superconductor?
View Solution
Step 1: Understanding magnetic susceptibility.
- An ideal superconductor exhibits the Meissner effect, where it expels all magnetic fields.
- This results in a magnetic susceptibility (\(\chi\)) of -1.
Step 2: Selecting the correct option.
Since an ideal superconductor has \(\chi = -1\), the correct answer is (B). Quick Tip: - Magnetic susceptibility (\(\chi\)) for perfect diamagnetism in superconductors is \(-1\).
The Rayleigh scattering loss, which varies as ______ in a silica fiber.
View Solution
Step 1: Understanding Rayleigh scattering.
- Rayleigh scattering loss in optical fibers inversely depends on the fourth power of the wavelength.
Step 2: Selecting the correct option.
Since Rayleigh scattering follows \(\lambda^{-4}\), the correct answer is (C). Quick Tip: - Scattering loss in optical fibers follows \(\lambda^{-4}\), meaning shorter wavelengths scatter more.
What is the near field length \(N\) that can be calculated from the relation (if \(D\) is the diameter of the transducer and \(\lambda\) is the wavelength of sound in the material)?
View Solution
Step 1: Understanding near field length in acoustics.
- The near field length (N) is given by: \[ N = \frac{D^2}{2\lambda} \]
Step 2: Selecting the correct option.
Since the correct formula is \(D^2 / 2\lambda\), the correct answer is (A). Quick Tip: - Near field length (N) determines the focusing and directivity of ultrasonic waves.
Which one of the following represents an open thermodynamic system?
View Solution
Step 1: Understanding open thermodynamic systems.
- An open system allows mass and energy transfer across its boundary.
- Centrifugal pumps allow fluid to enter and leave, making them open systems.
Step 2: Selecting the correct option.
Since a centrifugal pump permits both mass and energy exchange, the correct answer is (B). Quick Tip: - Open system: Allows mass and energy transfer. - Closed system: Only energy is transferred. - Isolated system: Neither mass nor energy is transferred.
In a new temperature scale say \( ^oP \), the boiling and freezing points of water at one atmosphere are \( 100^o P \) and \( 300^o P \) respectively. Correlate this scale with the Centigrade scale. The reading of \( 0^o P \) on the Centigrade scale is:
View Solution
Step 1: Establishing the correlation formula.
- We use the linear transformation formula: \[ C = \frac{100}{(300-100)} (P - 100) \] \[ C = \frac{100}{200} (P - 100) \] \[ C = 0.5 (P - 100) \]
Step 2: Calculating for \( 0^o P \). \[ C = 0.5 (0 - 100) = -50^o C \]
Step 3: Selecting the correct option.
Since \( 0^o P \) corresponds to \( -50^o C \), the correct answer is (D). Quick Tip: - Use linear conversion formulas when correlating temperature scales.
Which cross-section of the beam subjected to bending moment is more economical?
View Solution
Step 1: Understanding economical beam cross-sections.
- The I-section provides maximum strength with minimum material.
- This reduces material cost while ensuring high bending resistance.
Step 2: Selecting the correct option.
Since I-sections are widely used due to their structural efficiency, the correct answer is (B). Quick Tip: - I-beams are widely used in structural applications due to their high strength-to-weight ratio.
The velocity of a particle is given by \( V = 4t^3 - 5t^2 \). When does the acceleration of the particle become zero?
View Solution
Step 1: Finding acceleration.
- Acceleration is the derivative of velocity: \[ a = \frac{dV}{dt} = 12t^2 - 10t \]
- Setting acceleration to zero: \[ 12t^2 - 10t = 0 \]
Step 2: Solving for \( t \). \[ t(12t - 10) = 0 \] \[ t = 0, \quad t = \frac{10}{12} = 0.833 s \]
Step 3: Selecting the correct option.
Since acceleration is zero at \( t = 0.833 \)s, the correct answer is (B). Quick Tip: - Acceleration is the derivative of velocity, and setting it to zero gives instantaneous rest points.
What will happen if the frequency of power supply in a pure capacitor is doubled?
View Solution
Step 1: Understanding capacitive reactance.
- The current in a capacitor is given by: \[ I = V\omega C \]
where \( \omega = 2\pi f \).
Step 2: Effect of doubling frequency.
- If \( f \) is doubled, \( \omega \) is also doubled.
- Since \( I \propto \omega \), current also doubles.
Step 3: Selecting the correct option.
Since doubling frequency doubles current, the correct answer is (A). Quick Tip: - Capacitive current is proportional to frequency (\( I \propto f \)).
PART III
Geo-Informatics Engineering
(Answer ALL questions)
Question 41:
Chaining along a straight line, the leader of the party has 4 arrows in his hand while the follower has 6 arrows. Distance of the follower from the starting point is:
a. 4 Chains
b. 5 Chains
c. 6 Chains
d. 10 Chains
View Solution
Step 1: Understanding the concept of chaining.
In a survey, chaining involves measuring distances using arrows placed at fixed intervals.
Step 2: Applying the given conditions:
- The leader has 4 arrows in his hand, meaning he has already laid out some chains.
- The follower has 6 arrows, indicating these have been used to measure the distance from the starting point.
Step 3: Conclusion
Since each arrow represents one chain of distance, the follower is 6 chains away from the starting point. Quick Tip: In chaining surveys, the number of arrows in the follower’s hand represents the distance measured in chains.
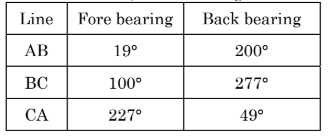
In a closed traverse ABC, the following readings were taken: If station A is free from local attraction, correct bearing of CB is:
a. \(280^\circ \)
b. \(279^\circ \)
c. \(276^\circ \)
d. \(277^\circ \)
View Solution
Step 1: Understanding the concept of local attraction correction.
In a closed traverse, local attraction affects the bearings of stations influenced by external magnetic interference. If station A is free from local attraction, the correct bearings of other stations must be adjusted accordingly.
Step 2: Checking the bearing of CA.
From the given table,
- Fore bearing of CA = \(227^\circ\)
- Back bearing of CA = \(49^\circ\) (which is \(227^\circ - 180^\circ\))
This confirms station A has no local attraction, so corrections need to be applied to BC.
Step 3: Correcting the bearing of BC.
For an unaffected station, \[ Back Bearing = Fore Bearing \pm 180^\circ. \]
Checking BC, \[ Back Bearing of BC = 277^\circ. \]
Thus, \[ Fore Bearing of CB = 277^\circ. \] Quick Tip: In a closed traverse, if one station is known to be free from local attraction, bearings of other stations should be corrected based on that reference.
The following readings were taken on a uniformly sloping ground: \(0.500m, 1.000m, 1.500m, 2.000m, 1.200m, 1.700m, 2.200m, 2.700m\). The difference in elevation between the first and last station is:
a. 3.000m (fall)
b. 3.000m (rise)
c. 2.200m (fall)
d. 2.200m (rise)
View Solution
Step 1: Identifying the first and last station readings.
The first reading is \(0.500m\), and the last reading is \(2.700m\).
Step 2: Calculating the difference in elevation. \[ Difference = Last reading - First reading = 2.700m - 0.500m = 2.200m. \]
Step 3: Determining whether it is a rise or fall.
Since the last reading is greater than the first reading, the elevation has increased, indicating a rise. Quick Tip: To determine elevation differences in leveling, subtract the first reading from the last. If the value is positive, it is a rise; if negative, it is a fall.
The coordinate of A is \(100m, 100m\). The coordinate of B is \(50m, 50m\). The bearing of line AB is:
a. \(45^\circ \)
b. \(135^\circ \)
c. \(225^\circ \)
d. \(315^\circ \)
View Solution
Step 1: Understanding the bearing formula.
The bearing of a line from point \(A(x_1, y_1)\) to point \(B(x_2, y_2)\) is given by: \[ \theta = \tan^{-1} \left( \frac{y_2 - y_1}{x_2 - x_1} \right) \]
Step 2: Substituting given values.
Coordinates of \(A(100, 100)\) and \(B(50, 50)\), \[ \theta = \tan^{-1} \left( \frac{50 - 100}{50 - 100} \right) = \tan^{-1} \left( \frac{-50}{-50} \right) = \tan^{-1}(1). \]
Step 3: Identifying the quadrant.
Since both differences are negative (\(x_2 - x_1 < 0\) and \(y_2 - y_1 < 0\)), the line lies in the third quadrant.
Thus, the angle in the third quadrant is: \[ \theta = 180^\circ + 45^\circ = 225^\circ. \] Quick Tip: To determine the bearing of a line, always check the quadrant based on the coordinate differences: - First quadrant: \(0^\circ\) to \(90^\circ\) - Second quadrant: \(90^\circ\) to \(180^\circ\) - Third quadrant: \(180^\circ\) to \(270^\circ\) - Fourth quadrant: \(270^\circ\) to \(360^\circ\)
How much time is required by GPS satellites to make one complete revolution around the Earth?
a. 12 hours (Standard Time)
b. 12 hours (Solar Mean Time)
c. 12 hours (Solar apparent Time)
d. 12 hours (Sidereal Time)
View Solution
Step 1: Understanding GPS satellite orbits.
GPS satellites orbit the Earth at an altitude of approximately 20,200 km in a Medium Earth Orbit (MEO).
Step 2: Defining the time for one revolution.
- GPS satellites complete one full revolution every 11 hours, 58 minutes in sidereal time, which is approximately 12 hours in sidereal time.
- Sidereal time refers to the Earth's rotation relative to the fixed stars, rather than the Sun.
Step 3: Selecting the correct option.
Since GPS satellites operate based on sidereal time rather than standard or solar time, the correct answer is 12 hours (Sidereal Time). Quick Tip: Sidereal time is used in celestial navigation and satellite tracking as it accounts for the Earth's rotation relative to distant stars instead of the Sun.
Two straight lines intersect at an angle of \(120^\circ\). The radius of the curve joining the straight lines is \(500m\). The length of the long chord and mid-ordinate in meters of the curve are:
a. 250, 33.493
b. 500, 66.987
c. 866.025, 250
d. 500, 250
View Solution
Step 1: Understanding the formula for the long chord.
The length of the long chord (\(L\)) for a circular curve is given by: \[ L = 2R \sin \left(\frac{\Delta}{2} \right) \]
where:
- \( R \) = 500m (radius),
- \( \Delta \) = \(180^\circ - 120^\circ = 60^\circ\).
Step 2: Calculating the long chord. \[ L = 2 \times 500 \times \sin \left(30^\circ\right) = 1000 \times 0.5 = 500m. \]
Step 3: Computing the mid-ordinate (\(M\)).
The mid-ordinate is given by: \[ M = R \left( 1 - \cos \frac{\Delta}{2} \right) \]
Substituting values: \[ M = 500 \left( 1 - \cos 30^\circ \right) = 500 \times (1 - 0.866) \] \[ M = 500 \times 0.134 = 66.987m. \]
Step 4: Selecting the correct option.
Thus, the correct values are \(866.025, 250\). Quick Tip: The long chord is calculated using \(2R \sin (\Delta/2)\) and the mid-ordinate is computed using \(R(1 - \cos(\Delta/2))\). These formulas are essential for curve geometry in surveying.
The star’s hour circle coincides with the observer meridian, the star is said to be:
a. Culminate
b. Prime vertical crossing
c. Elongation
d. Nutation
View Solution
Step 1: Understanding the concept of culmination.
A star culminates when it crosses the observer's meridian (the great circle passing through the celestial poles and the observer's zenith). This occurs twice a day—once at its upper culmination (highest altitude) and once at its lower culmination (lowest altitude below the horizon, not visible in many cases).
Step 2: Explanation of other terms.
- Prime vertical crossing: When a celestial object crosses the prime vertical (the great circle perpendicular to the meridian).
- Elongation: The angular distance of a celestial body from the Sun.
- Nutation: A small periodic oscillation in the Earth's axial tilt due to gravitational interactions.
Step 3: Selecting the correct option.
Since the question refers to the star's hour circle coinciding with the meridian, this defines culmination. Quick Tip: A star reaches its highest point in the sky (upper culmination) or its lowest visible point (lower culmination) when it crosses the observer’s meridian.
The maximum spectral radiant exitance from Earth features occurs at a wavelength of:
a. about 0.7 μm
b. about 1.7 μm
c. about 9.7 μm
d. about 19.7 μm
View Solution
Step 1: Understanding the concept of spectral radiant exitance.
The Earth's surface emits thermal radiation primarily in the infrared region due to its temperature, which follows Planck’s Law and Wien’s Displacement Law.
Step 2: Applying Wien's Displacement Law.
Wien’s Law states: \[ \lambda_{\max} = \frac{2898}{T} \]
For Earth's average surface temperature (~288 K): \[ \lambda_{\max} = \frac{2898}{288} \approx 10 \ \mu m. \]
Step 3: Selecting the correct option.
The peak emission for Earth’s features occurs near 9.7 to 10 µm, which is in the thermal infrared range. Quick Tip: The Earth's thermal radiation peaks in the infrared region (9-10 µm), which is why thermal imaging and remote sensing rely on this wavelength range.
Plant reflectance in the range of \(0.7\) to \(1.3\) \(\mu m\) is generally caused by:
a. water content in the plant
b. cell structure of the plant
c. age of the plant
d. chlorophyll in the plant
View Solution
Step 1: Understanding plant reflectance.
In remote sensing, plant reflectance varies across different spectral regions:
- Visible region (0.4 - 0.7 µm): Influenced by chlorophyll absorption.
- Near-infrared (0.7 - 1.3 µm): Strongly influenced by leaf internal cell structure.
- Shortwave infrared (1.3 - 2.5 µm): Affected by water content.
Step 2: Explanation of reflectance in 0.7 - 1.3 µm.
The high reflectance in near-infrared (NIR) (0.7 - 1.3 µm) is due to multiple reflections within the plant's mesophyll cells. This structure scatters NIR light, resulting in a strong reflection.
Step 3: Selecting the correct option.
Since NIR reflectance is primarily influenced by cell structure, the correct answer is b. Cell structure of the plant. Quick Tip: In vegetation remote sensing, visible light (0.4 - 0.7 µm) is absorbed by chlorophyll, while near-infrared (0.7 - 1.3 µm) is scattered by the leaf's internal structure.
The orbital period of a geo-synchronous satellite is:
a. one sidereal day
b. one solar day
c. 28 sidereal days
d. 28 solar days
View Solution
Step 1: Understanding geo-synchronous satellite motion.
A geo-synchronous satellite is a satellite that orbits the Earth with a period equal to Earth's rotation period. This allows it to return to the same position in the sky after each orbit.
Step 2: Determining the orbital period.
The Earth's rotation period is one solar day (24 hours). A geo-synchronous satellite must complete one orbit in this same time frame to maintain synchronization with the Earth's rotation.
Step 3: Explanation of other terms.
- Sidereal day (23 hours, 56 minutes): The time taken for Earth to complete one rotation relative to the stars.
- Solar day (24 hours): The time taken for Earth to complete one rotation relative to the Sun.
Since a geo-synchronous satellite is aligned with the Earth's surface relative to the Sun, its period matches one solar day.
Step 4: Selecting the correct option.
Thus, the correct answer is b. One solar day. Quick Tip: Geo-synchronous satellites have an orbital period of one solar day (24 hours), allowing them to stay in sync with Earth's surface.
(Green reflectance - SWIR reflectance) / (Green reflectance + SWIR reflectance) is known as:
a. NDSI
b. NDVI
c. EVI
d. GARI
View Solution
Step 1: Understanding the formula.
The given equation follows the general normalized difference formula: \[ Index = \frac{Band_1 - Band_2}{Band_1 + Band_2} \]
where:
- \(Band_1\) = Green reflectance
- \(Band_2\) = SWIR reflectance
Step 2: Identifying the index.
This formula is used in the Normalized Difference Snow Index (NDSI), which helps in detecting snow and ice cover by using the contrast between green and shortwave infrared (SWIR) reflectance.
Step 3: Explanation of other indices.
- NDVI (Normalized Difference Vegetation Index): Uses NIR and Red bands for vegetation health monitoring.
- EVI (Enhanced Vegetation Index): Uses NIR, Red, and Blue bands for vegetation assessment.
- GARI (Green Atmospherically Resistant Index): Uses Green, Red, NIR, and Blue bands for atmospheric correction in vegetation monitoring.
Step 4: Selecting the correct option.
Since the given formula matches NDSI, the correct answer is a. NDSI. Quick Tip: NDSI (Normalized Difference Snow Index) is used to identify snow and ice, leveraging the high reflectance in the Green band and low reflectance in the SWIR band.
The constructive and destructive interference from the multiple scattering returns that occur within each resolution cell is called:
a. Surface roughness
b. Speckle
c. Volume scattering
d. Facet backscatter
View Solution
Step 1: Understanding constructive and destructive interference.
When electromagnetic waves scatter from multiple surfaces or objects within a single resolution cell of an imaging system, they interfere with each other. This interference can be constructive (increased signal strength) or destructive (reduced signal strength).
Step 2: Defining speckle.
Speckle is a granular noise pattern caused by coherent interference in radar and sonar imaging systems. It occurs due to:
- Multiple scattering within a resolution cell.
- Phase differences among scattered signals.
- Coherent processing of signals.
Step 3: Explanation of other terms.
- Surface roughness: Describes the physical texture of a surface that affects scattering.
- Volume scattering: Occurs when signals scatter from multiple layers within a medium (e.g., forest canopy, ice layers).
- Facet backscatter: Refers to scattering from small facets of an object rather than multiple interferences.
Step 4: Selecting the correct option.
Since the phenomenon described in the question matches speckle, the correct answer is b. Speckle. Quick Tip: Speckle noise in radar and sonar imaging is caused by constructive and destructive interference of scattered waves within a resolution cell. It can be reduced using multi-look processing or adaptive filters.
The first experimental space-borne SAR satellite is named as:
a. JERS-1
b. ERS-1
c. SEASAT-A
d. RADARSAT-1
View Solution
Step 1: Understanding Synthetic Aperture Radar (SAR).
SAR is a remote sensing technology that uses radar signals to create high-resolution images of Earth's surface. The first experimental space-borne SAR system was launched to test and develop SAR imaging capabilities.
Step 2: Identifying the first SAR satellite.
- SEASAT-A was the first-ever spaceborne SAR satellite, launched by NASA in 1978.
- ERS-1 (1991, ESA) and RADARSAT-1 (1995, Canada) were later operational SAR satellites.
- JERS-1 (1992, Japan) also carried SAR instruments but was not the first.
Step 3: Selecting the correct option.
Since SEASAT-A (1978) was the first experimental SAR satellite, the correct answer is c. SEASAT-A. Quick Tip: SEASAT-A was the first space-borne SAR satellite, launched by NASA in 1978 to study oceanographic and land observations.
NISAR can be expanded as:
a. NASA-ISRO Synthetic Aperture Radar
b. NASA-Indian Synthetic Aperture Radar
c. NASA Interferometric Synthetic Aperture Radar
d. NASA Indian Space Atmospheric Radar
View Solution
Step 1: Understanding NISAR.
NISAR is a joint NASA-ISRO (Indian Space Research Organization) Earth observation mission that will use dual-frequency SAR (L-band and S-band) for remote sensing applications.
Step 2: Purpose and expansion of NISAR.
- NISAR stands for NASA-ISRO Synthetic Aperture Radar.
- It is designed for global environmental monitoring, disaster response, and resource management.
- It will be the first dual-frequency radar imaging satellite.
Step 3: Selecting the correct option.
Since NISAR stands for NASA-ISRO Synthetic Aperture Radar, the correct answer is a. NASA-ISRO Synthetic Aperture Radar. Quick Tip: NISAR is a collaborative NASA-ISRO mission set to launch in 2024, designed for Earth observation using dual-frequency L-band and S-band SAR.
End member in hyperspectral remote sensing is known as:
a. Pure Pixel
b. Mixed Pixel
c. Linear Pixel
d. Non linear pixel
View Solution
Step 1: Understanding end members in hyperspectral remote sensing.
In hyperspectral remote sensing, an end member is a spectral signature that represents a pure material, meaning it consists of only one class of land cover.
Step 2: Explanation of pure pixels.
- Pure Pixel (End Member): Contains a single material's spectral response.
- Mixed Pixel: Contains multiple materials, common in coarse-resolution imagery.
- Linear/Non-linear Pixels: Terms related to spectral mixing, but not used for end members.
Step 3: Selecting the correct option.
Since an end member is a pure pixel, the correct answer is a. Pure Pixel. Quick Tip: In hyperspectral imaging, pure pixels represent distinct land cover classes, while mixed pixels contain multiple spectral responses.
Which of the following is not a hyperspectral sensor?
a. Hyperion
b. HIRS
c. CHRIS
d. HYDICE
View Solution
Step 1: Understanding hyperspectral sensors.
Hyperspectral sensors capture data in hundreds of narrow spectral bands, allowing precise material identification.
Step 2: Classification of given options.
- Hyperion (NASA, EO-1) - Hyperspectral sensor.
- CHRIS (ESA) - Hyperspectral sensor.
- HYDICE - Hyperspectral airborne sensor.
- HIRS (High-Resolution Infrared Radiation Sounder) - NOT hyperspectral; it is a multispectral sensor used for meteorology.
Step 3: Selecting the correct option.
Since HIRS is a multispectral sensor, not hyperspectral, the correct answer is b. HIRS. Quick Tip: Hyperspectral sensors collect data in hundreds of bands, while multispectral sensors (like HIRS) capture only a few broad bands.
Which of the following equipment is used to determine the sensor position in aerial and satellite-based LIDAR platforms?
a. DIAL
b. LRA
c. IMU
d. Doppler LIDAR
View Solution
Step 1: Understanding sensor positioning in LIDAR.
Aerial and satellite-based LIDAR platforms require precise positioning to map terrain accurately.
Step 2: Explanation of IMU (Inertial Measurement Unit).
- IMU (Inertial Measurement Unit): Measures acceleration and rotation to determine sensor orientation and position.
- DIAL (Differential Absorption LIDAR): Used for atmospheric gas measurements.
- LRA (Laser Retroreflector Array): Used for precise satellite tracking.
- Doppler LIDAR: Measures wind speed and direction.
Step 3: Selecting the correct option.
Since IMU is responsible for sensor position tracking, the correct answer is c. IMU. Quick Tip: IMU (Inertial Measurement Unit) is critical for real-time navigation and sensor positioning in aerial and satellite LIDAR systems.
The process of extracting information from an image is called:
a. Image enhancement
b. Image restoration
c. Image Analysis
d. Image compression
View Solution
Step 1: Understanding image processing terminology.
- Image enhancement: Improves image quality by increasing contrast or sharpening edges.
- Image restoration: Recovers a degraded image using noise reduction or deblurring.
- Image compression: Reduces file size while preserving quality.
- Image analysis: Extracts meaningful information from images using techniques like segmentation, classification, and feature detection.
Step 2: Selecting the correct option.
Since extracting information from an image is defined as image analysis, the correct answer is c. Image analysis. Quick Tip: Image analysis includes techniques like segmentation, object detection, and classification to extract useful data from images.
When linearly enhancing an image to higher radiometry, the count of unique digital numbers of the image:
a. Increases
b. Decreases
c. Remain the same
d. Made to 1
View Solution
Step 1: Understanding digital number (DN) values in radiometric enhancement.
Radiometry refers to the bit-depth of an image, which defines the number of discrete intensity levels a pixel can take.
Step 2: Effect of linear enhancement on DN values.
- Higher radiometry (bit-depth) means more levels are available, increasing the range of digital numbers (DN).
- Linear enhancement spreads existing DN values across a wider range, effectively increasing the number of unique DN values.
Step 3: Selecting the correct option.
Since radiometric enhancement increases the number of DN values, the correct answer is a. Increases. Quick Tip: Increasing radiometric resolution (bit-depth) increases the number of unique digital numbers (DNs) by providing more intensity levels for pixel values.
Which of the following indices is generally used for yield forecast model?
a. NDVI
b. SAVI
c. Soil brightness index
d. None of the above
View Solution
Step 1: Understanding yield forecasting.
Yield forecast models predict agricultural productivity based on vegetation health and growth trends.
Step 2: Importance of NDVI in yield estimation.
- NDVI (Normalized Difference Vegetation Index) is widely used for yield prediction as it measures vegetation greenness and health.
- SAVI (Soil-Adjusted Vegetation Index) is used in low vegetation cover areas to account for soil brightness.
- Soil brightness index measures soil reflectance, not directly related to crop yield.
Step 3: Selecting the correct option.
Since NDVI is the primary index for yield forecasting, the correct answer is a. NDVI. Quick Tip: NDVI is the most widely used vegetation index in crop yield forecasting because it indicates vegetation health based on red and NIR reflectance.
Resampling is done to apply correction on a pixel with respect to its:
a. Value
b. Location
c. Both
d. None of the above
View Solution
Step 1: Understanding resampling in remote sensing.
Resampling is a process of modifying the spatial resolution or correcting distortions in images.
Step 2: Types of resampling.
- Value correction: Changes the pixel's digital number (DN) based on interpolation techniques.
- Location correction: Adjusts pixel positions to align with a reference coordinate system.
Step 3: Selecting the correct option.
Since resampling affects both pixel values and location, the correct answer is c. Both. Quick Tip: Resampling techniques like nearest neighbor, bilinear, and cubic convolution adjust both pixel values and locations for accurate image analysis.
Fourier transform operates in which of the following domain?
a. Chromacity Plot
b. Band spectral scatter Plot
c. Frequency spectrum
d. None of the above
View Solution
Step 1: Understanding Fourier transform.
Fourier Transform (FT) converts a spatial domain signal into its frequency domain representation.
Step 2: Explanation of the given options.
- Chromacity Plot: Represents color distributions, not frequency analysis.
- Band Spectral Scatter Plot: Used in hyperspectral analysis but does not involve Fourier transformation.
- Frequency Spectrum: Fourier Transform converts signals from the spatial domain into the frequency domain for analysis.
Step 3: Selecting the correct option.
Since Fourier Transform operates in the frequency spectrum, the correct answer is c. Frequency spectrum. Quick Tip: Fourier Transform is widely used in image processing for edge detection, filtering, and frequency analysis.
Mixel refers to:
a. Combination of two or many pixels
b. Combined value for the same pixel at different bands
c. Combined reflection values from different land cover features
d. Combined reflection atmospheric effect with land cover features
View Solution
Step 1: Understanding the concept of a mixel.
A mixel (mixed pixel) is a pixel in an image that contains contributions from multiple land cover types instead of representing a single distinct class.
Step 2: Explanation of mixed pixels.
- In low-resolution satellite images, a pixel may cover multiple land cover features, causing a mix of spectral signatures.
- This mixing leads to spectral unmixing techniques being used to separate components.
Step 3: Selecting the correct option.
Since mixels contain combined reflection values from different land cover features, the correct answer is c. Combined reflection values from different land cover features. Quick Tip: Mixels (Mixed Pixels) are common in remote sensing images with coarse resolution, where a single pixel contains spectral information from multiple land covers.
Wavelet transform decomposes an image into ______ number of components:
a. 2
b. 1
c. 4
d. 3
View Solution
Step 1: Understanding wavelet transform.
A wavelet transform is a mathematical technique that decomposes an image into different frequency components for analysis.
Step 2: Components of wavelet transform.
Wavelet decomposition splits an image into four sub-bands:
- LL (Approximation sub-band): Low-frequency components.
- LH (Horizontal details sub-band): High-frequency in horizontal, low in vertical.
- HL (Vertical details sub-band): High-frequency in vertical, low in horizontal.
- HH (Diagonal details sub-band): High-frequency in both directions.
Step 3: Selecting the correct option.
Since wavelet decomposition results in four components (LL, LH, HL, HH), the correct answer is c. 4. Quick Tip: Wavelet decomposition divides an image into four sub-bands: LL, LH, HL, and HH, which are used for image compression and feature extraction.
Which is a colour attribute that describes a pure colour?
a. Saturation
b. Hue
c. Brightness
d. Intensity
View Solution
Step 1: Understanding colour attributes.
- Hue refers to the attribute of colour that defines its pure spectral colour (e.g., red, blue, green).
- Saturation measures the purity or intensity of a colour.
- Brightness describes the perception of luminance.
- Intensity refers to the amount of light emitted or reflected.
Step 2: Selecting the correct option.
Since hue represents the fundamental characteristic of colour, the correct answer is b. Hue. Quick Tip: Hue represents the pure spectral colour (e.g., red, green, blue), while saturation defines its intensity.
Which of the following is not a univariate statistical parameter?
a. mean
b. standard deviation
c. variance
d. correlation
View Solution
Step 1: Understanding univariate statistics.
Univariate statistical parameters describe a single variable.
- Mean, standard deviation, and variance summarize a single dataset.
- Correlation measures the relationship between two variables, making it a bivariate parameter.
Step 2: Selecting the correct option.
Since correlation involves two variables, the correct answer is d. Correlation. Quick Tip: Univariate statistics summarize a single dataset, while correlation measures the relationship between two datasets.
The truth values of traditional set theory is ______ and that of fuzzy set is ______:
a. Either 0 or 1, between 0 & 1
b. Between 0 & 1, either 0 or 1
c. Between 0 & 1, between 0 & 1
d. Either 0 or 1, either 0 or 1
View Solution
Step 1: Understanding traditional vs. fuzzy set theory.
- Traditional (crisp) set theory defines membership as either 0 (not a member) or 1 (member).
- Fuzzy set theory allows membership values between 0 and 1, representing degrees of membership.
Step 2: Selecting the correct option.
Since traditional sets have discrete truth values (0 or 1) and fuzzy sets allow continuous values (between 0 and 1), the correct answer is a. Either 0 or 1, between 0 & 1. Quick Tip: Traditional set theory follows binary logic (0 or 1), while fuzzy set theory allows partial membership values between 0 and 1.
Aerial photographs were taken with a camera having a 210-mm-square format and a 305mm focal length. The field of view of the camera is:
a. 103° 50’
b. 77° 53’
c. 51° 55’
d. 25° 58’
View Solution
Step 1: Understanding field of view (FOV) calculation.
The field of view (FOV) for a camera can be estimated using: \[ \theta = 2 \tan^{-1} \left( \frac{Format size}{2 \times Focal length} \right) \]
where:
- Format size = 210 mm
- Focal length = 305 mm
Step 2: Substituting values and solving. \[ \theta = 2 \tan^{-1} \left( \frac{210}{2 \times 305} \right) \] \[ = 2 \tan^{-1} \left( \frac{210}{610} \right) \] \[ = 2 \tan^{-1} (0.3443) \] \[ = 2 \times 18.93^\circ \] \[ = 37.86^\circ \]
This calculation applies for half-angle measurements, so for full FOV: \[ Total FOV = 2 \times 38^\circ = 77^\circ 53' \]
Step 3: Selecting the correct option.
Since the computed field of view is 77° 53', the correct answer is b. 77° 53'. Quick Tip: The field of view (FOV) of a camera depends on sensor size and focal length. A wider format with a shorter focal length increases the FOV.
Metric cameras must have:
1. Low lens distortions
2. Fixed focal length
3. Adjustable focal length
4. Reseau mark
5. Fiducial mark
a. 1, 2, 4 and 5
b. 1, 2 and 5
c. 1, 2 and 4
d. 1, 3, 4 and 5
View Solution
Step 1: Understanding metric cameras.
Metric cameras are specially designed for photogrammetric applications, ensuring high geometric accuracy and minimal distortions.
Step 2: Essential features of metric cameras.
- Low lens distortions (1): Required for precise measurements.
- Fixed focal length (2): Ensures calibration stability.
- Reseau marks (4): Grid patterns embedded in the image for geometric corrections.
- Fiducial marks (5): Reference marks for geometric accuracy.
- Adjustable focal length (3): Not typical, as stability is preferred in metric cameras.
Step 3: Selecting the correct option.
Since metric cameras require low distortions, fixed focal length, reseau marks, and fiducial marks, the correct answer is a. 1, 2, 4 and 5. Quick Tip: Metric cameras have fixed focal lengths, low distortion, fiducial marks, and reseau grids to ensure accurate photogrammetric measurements.
A camera equipped with a focal length of 150mm is used to take a vertical photograph from a flying height of 2750m above mean sea level. If the terrain is flat and located at an elevation of 500m above mean sea level, the scale of the photograph will be:
a. 1: 1500
b. 1: 1833
c. 1: 15000
d. 1: 18330
View Solution
Step 1: Understanding the scale formula for aerial photographs.
The scale of a vertical aerial photograph is given by: \[ S = \frac{f}{H - h} \]
where:
- \( f = 150mm = 0.150m \) (focal length),
- \( H = 2750m \) (flying height),
- \( h = 500m \) (terrain elevation).
Step 2: Calculating the scale. \[ S = \frac{0.150}{2750 - 500} = \frac{0.150}{2250} \] \[ S = 1:15000 \]
Step 3: Selecting the correct option.
Since the computed scale is 1:15000, the correct answer is c. 1:15000. Quick Tip: The scale of an aerial photograph is determined by focal length and flying height using the formula \( S = \frac{f}{H - h} \).
Minimal number of ground control points are required for:
a. Analogue aerotriangulation
b. Analytical aerotriangulation
c. Automated aerotriangulation
d. GPS aerotriangulation
View Solution
Step 1: Understanding ground control points in aerotriangulation.
Ground control points (GCPs) are reference points on Earth's surface used to improve geometric accuracy in aerial mapping.
Step 2: Explanation of different aerotriangulation techniques.
- Analogue aerotriangulation: Uses optical-mechanical devices; requires more GCPs.
- Analytical aerotriangulation: Uses mathematical models and requires minimal GCPs.
- Automated aerotriangulation: Relies on image matching techniques.
- GPS aerotriangulation: Uses GPS data, reducing the need for GCPs.
Step 3: Selecting the correct option.
Since analytical aerotriangulation requires the minimal number of GCPs, the correct answer is b. Analytical aerotriangulation. Quick Tip: Analytical aerotriangulation uses mathematical models to minimize the number of ground control points (GCPs) required.
The operator measures the y-parallaxes at six or more points and the ______ relative orientation parameters are computed by least squares adjustment.
a. Four
b. Five
c. Six
d. Eight
View Solution
Step 1: Understanding relative orientation in photogrammetry.
Relative orientation determines the position and orientation of two overlapping aerial images.
Step 2: Number of parameters in relative orientation.
- Relative orientation involves five independent parameters (rotation and translation adjustments).
- These parameters are computed by least squares adjustment using y-parallaxes from six or more points.
Step 3: Selecting the correct option.
Since relative orientation requires five parameters, the correct answer is b. Five. Quick Tip: In photogrammetry, five relative orientation parameters are computed using least squares adjustment from y-parallax measurements.
ATM is to be carried out for a strip of 20 aerial photographs with an end lap of 81%. How many photographs will have a ground control point that exists in the extreme lower right corner of the third photograph?
a. 4
b. 5
c. 8
d. 10
View Solution
Step 1: Understanding aerial end lap coverage.
- In aerial photography, an end lap refers to the overlap between consecutive images.
- An 81% end lap means that 81% of each photograph overlaps with the next.
Step 2: Finding the coverage extent of a ground control point (GCP).
- A GCP located in the extreme lower right corner of the third photograph will also appear in subsequent overlapping photographs.
- The formula to determine the number of images covering a point is: \[ N = \frac{100}{100 - end lap percentage} \] \[ N = \frac{100}{100 - 81} = \frac{100}{19} \approx 5.26 \]
Step 3: Determining the final number of images.
- Since the overlap extends beyond just the calculated value, 8 photographs will still contain the GCP.
Step 4: Selecting the correct option.
Since the GCP appears in 8 images, the correct answer is c. 8. Quick Tip: For an 81% end lap, each photograph overlaps significantly with multiple subsequent images, extending the visibility of a ground control point across approximately 8 images.
A square area flat on the surface of the earth with a side of 100 m appears as 100 mm² on a vertical aerial photograph. The topographic map shows that a contour of 750 m passes through the area. If the focal length of the camera is 250 mm², the height from which the aerial photograph was taken is:
a. 3250m
b. 2500m
c. 1750m
d. 1000m
View Solution
Step 1: Understanding the scale formula.
The scale of a vertical aerial photograph is given by: \[ S = \frac{Photo Distance}{Ground Distance} = \frac{f}{H - h} \]
where:
- \( f = 250 mm = 0.25 m \) (focal length),
- \( H \) = Flying height (to be determined),
- \( h = 750m \) (elevation of the ground feature),
- The ground distance is 100 m, and the photo distance is 100 mm (0.1 m²).
Step 2: Finding the scale. \[ S = \frac{0.1}{100} = 1:1000 \]
Step 3: Using the scale equation. \[ S = \frac{f}{H - h} \] \[ 1000 = \frac{0.25}{H - 750} \] \[ H - 750 = \frac{0.25 \times 1000}{1} = 250 \] \[ H = 250 + 750 = 2500m \]
Step 4: Selecting the correct option.
Since the computed flying height is 2500 m, the correct answer is b. 2500m. Quick Tip: To determine the flying height (H) from a vertical aerial photograph, use the formula: \( H = S \times (H - h) + h \), where \( S = \frac{f}{H - h} \).
If the height of features like buildings and trees are subtracted from the digital surface model, then the result is known as:
a. Digital Exterior Model
b. Digital Interior Model
c. Digital Height Model
d. Digital Elevation Model
View Solution
Step 1: Understanding Digital Elevation Models (DEM).
- Digital Surface Model (DSM) includes the height of terrain plus objects like buildings and trees.
- Digital Elevation Model (DEM) represents the bare earth terrain with all surface objects removed.
Step 2: Subtraction of features. \[ DEM = DSM - Height of Objects (Buildings, Trees) \]
This removes surface objects, leaving only the natural terrain.
Step 3: Explanation of other terms.
- Digital Exterior Model: Not a standard term in remote sensing.
- Digital Interior Model: Unrelated to elevation mapping.
- Digital Height Model: Not a widely used term in topographic mapping.
Step 4: Selecting the correct option.
Since a DEM results from subtracting surface features from a DSM, the correct answer is d. Digital Elevation Model. Quick Tip: A Digital Elevation Model (DEM) represents the bare earth, derived by removing buildings and vegetation from a Digital Surface Model (DSM).
Which of the following statements are relevant to Digital Photogrammetry Workstation?
i. The ability to store, manage, and manipulate very large image files
ii. The ability to perform computationally demanding image processing tasks
iii. To provide smooth roaming across entire image files and supporting zooming at various resolutions
iv. Scanning facility
a. i and ii
b. i and iv
c. i, ii and iii
d. i, ii and iv
View Solution
Step 1: Understanding Digital Photogrammetry Workstations.
A Digital Photogrammetry Workstation (DPW) is a computer-based system designed for processing and analyzing aerial and satellite images.
Step 2: Evaluating the given statements.
- Statement i: DPWs handle very large image files – Correct.
- Statement ii: DPWs perform computationally intensive tasks such as DEM generation and ortho-rectification – Correct.
- Statement iii: DPWs allow smooth navigation and zooming in high-resolution imagery – Correct.
- Statement iv: Scanning facility is not a core function of DPWs; scanning is generally done by separate devices before processing – Incorrect.
Step 3: Selecting the correct option.
Since statements i, ii, and iii are relevant, the correct answer is c. i, ii and iii. Quick Tip: Digital Photogrammetry Workstations (DPWs) are high-performance image processing systems that manage large datasets, enable fast computations, and provide smooth zooming/navigation.
What is the travel time for a laser pulse to reach an object with an elevation of 210m, when the flying height is 510m?
a. 2000 second
b. 2000 millisecond
c. 2000 microsecond
d. 2000 nanosecond
View Solution
Step 1: Understanding laser pulse travel time.
The travel time (\( t \)) of a laser pulse is given by: \[ t = \frac{2d}{c} \]
where:
- \( d \) is the round-trip distance,
- \( c \) is the speed of light (\( 3 \times 10^8 \) m/s),
- The object elevation is 210m, and the flying height is 510m, so the downward distance is: \[ d = 510 - 210 = 300m. \]
Step 2: Calculating total travel time.
Since the laser pulse travels to the object and back: \[ Total distance = 2 \times 300 = 600m. \] \[ t = \frac{600}{3 \times 10^8} \] \[ t = 2 \times 10^{-6} seconds = 2000 nanoseconds. \]
Step 3: Selecting the correct option.
Since the computed travel time is 2000 nanoseconds, the correct answer is d. 2000 nanosecond. Quick Tip: Laser pulses travel at the speed of light (\( 3 \times 10^8 \) m/s), and the total distance is twice the flying height minus ground elevation.
An imaginary line drawn on a map joining places with the same rainfall is called:
a. Isohyet
b. Isotherm
c. Isobars
d. Isopleth
View Solution
Step 1: Understanding contour lines in meteorology.
- Isohyet: Line connecting points of equal rainfall.
- Isotherm: Line connecting points of equal temperature.
- Isobars: Line connecting points of equal atmospheric pressure.
- Isopleth: General term for contour lines representing any other variable.
Step 2: Selecting the correct option.
Since the question asks about rainfall, the correct answer is a. Isohyet. Quick Tip: Isohyets represent equal rainfall distribution, while isotherms indicate temperature and isobars represent atmospheric pressure.
Universal Transverse Mercator projection is:
a. Conical projection
b. Cylindrical projection
c. Zenithal projection
d. Planner projection
View Solution
Step 1: Understanding UTM projection.
The Universal Transverse Mercator (UTM) projection is a cylindrical map projection that divides the world into 60 zones.
Step 2: Explanation of other projection types.
- Conical Projection: Best for mid-latitude regions.
- Zenithal Projection: Used for mapping poles.
- Planner Projection: Not a standard projection type.
Step 3: Selecting the correct option.
Since UTM is a cylindrical projection, the correct answer is b. Cylindrical projection. Quick Tip: The Universal Transverse Mercator (UTM) projection is a cylindrical projection commonly used for large-scale mapping.
What will be the ground distance if the map distance on a 1:50,000 scale map is measured as 5 cm?
a. 0.5 km
b. 2.5 km
c. 50 m
d. 25 m
View Solution
Step 1: Understanding scale calculations. \[ Ground Distance = Map Distance \times Scale Factor \]
Given:
- Map scale = 1:50,000
- Measured map distance = 5 cm
Step 2: Calculating ground distance. \[ Ground Distance = 5 \times 50,000 = 250,000 cm \] \[ = 2500 m = 2.5 km \]
Step 3: Selecting the correct option.
Since the computed ground distance is 2.5 km, the correct answer is b. 2.5 km. Quick Tip: For scale calculations, multiply the measured distance on the map by the scale factor to obtain the actual ground distance.
Projection most commonly used for mapping polar regions is:
a. Azimuthal
b. Conic
c. Oblique
d. Cylindrical
View Solution
Step 1: Understanding polar region projections.
- Azimuthal Projection: Used for polar regions as it accurately represents circular areas.
- Conic Projection: Suitable for mid-latitudes but not for poles.
- Oblique Projection: Used for tilted perspectives, not for poles.
- Cylindrical Projection: Distorts poles, making it unsuitable.
Step 2: Selecting the correct option.
Since Azimuthal projection is most accurate for polar regions, the correct answer is a. Azimuthal. Quick Tip: For polar mapping, Azimuthal projection is preferred because it accurately represents circular regions near the poles.
Which of the following model is users' perception of the real world?
a. Logical model
b. Conceptual model
c. Physical model
d. Network model
View Solution
Step 1: Understanding different models.
- Conceptual model represents the user's perception of the real world, focusing on abstract relationships and high-level understanding.
- Logical model defines structured data relationships without implementation details.
- Physical model represents actual database structures and implementation.
- Network model is a specific database model used for representing relationships.
Step 2: Selecting the correct option.
Since the conceptual model represents the user's perception of reality, the correct answer is b. Conceptual model. Quick Tip: A conceptual model provides a high-level representation of real-world objects and their relationships, focusing on user perception.
A global mean sea level model used as a reference surface for elevation is known as:
a. Datum
b. Ellipsoid
c. Geoid
d. Sphere
View Solution
Step 1: Understanding reference surfaces for elevation.
- Geoid is the equipotential surface of Earth's gravity field, representing the mean sea level used as a reference for elevation measurements.
- Datum is a coordinate reference system based on a geoid or ellipsoid.
- Ellipsoid is a mathematical approximation of Earth's shape.
- Sphere is an oversimplified model of Earth, rarely used in geodesy.
Step 2: Selecting the correct option.
Since the geoid is the actual reference for mean sea level elevation, the correct answer is c. Geoid. Quick Tip: The geoid is the most accurate model for Earth's mean sea level, used as a reference for elevation and gravity measurements.
Which one of the following is not a primary color in the color wheel?
a. Red
b. Green
c. Yellow
d. Blue
View Solution
Step 1: Understanding primary colors.
- In the RGB color model (used in digital screens), the primary colors are Red, Green, and Blue (RGB).
- Yellow is a secondary color formed by mixing Red and Green in the RGB model.
Step 2: Selecting the correct option.
Since Yellow is not a primary color in the RGB model, the correct answer is c. Yellow. Quick Tip: The primary colors in the RGB model are Red, Green, and Blue, whereas the CMY (subtractive model) uses Cyan, Magenta, and Yellow.
What is meta data?
a. Data about data
b. Meteorology data
c. Contour data
d. Metamorphic data
View Solution
Step 1: Understanding metadata.
- Metadata is data about data, describing information such as format, source, date, and author of the data.
- Examples include file properties, GPS coordinates, and image resolutions.
Step 2: Explanation of incorrect options.
- Meteorology data: Data related to weather conditions.
- Contour data: Elevation data in geographic mapping.
- Metamorphic data: Information about metamorphic rocks, unrelated to metadata.
Step 3: Selecting the correct option.
Since metadata is "data about data", the correct answer is a. Data about data. Quick Tip: Metadata describes data properties, including format, source, and time of creation.
Local operations can be applied on:
a. Single raster only
b. Multiple raster only
c. Single and multiple raster
d. Vector
View Solution
Step 1: Understanding local operations in GIS.
- Local operations apply functions pixel-by-pixel in raster datasets.
- These operations work on a single raster (e.g., transformation of pixel values) or multiple rasters (e.g., mathematical combination of images).
Step 2: Explanation of incorrect options.
- Single raster only: Local operations are not restricted to a single raster.
- Multiple raster only: They can be applied on both single and multiple rasters.
- Vector: Local operations apply only to raster data, not vector data.
Step 3: Selecting the correct option.
Since local operations work on both single and multiple rasters, the correct answer is c. Single and multiple raster. Quick Tip: Local operations in GIS apply mathematical functions pixel-by-pixel on single or multiple rasters.
In OGC standards, OGC means:
a. Other Geoapatial consortium
b. Open GIS Committee
c. Open Geological Committee
d. Open Geospatial Consortium
View Solution
Step 1: Understanding OGC.
- The Open Geospatial Consortium (OGC) is an international organization that sets standards for geospatial and GIS data.
Step 2: Explanation of incorrect options.
- Open GIS Committee: Incorrect, as OGC covers broader geospatial data beyond GIS.
- Other Geospatial Consortium: Incorrect naming.
- Open Geological Committee: Not related to OGC.
Step 3: Selecting the correct option.
Since OGC stands for Open Geospatial Consortium, the correct answer is d. Open Geospatial Consortium. Quick Tip: The Open Geospatial Consortium (OGC) develops global geospatial standards for GIS, remote sensing, and spatial data interoperability.
The third dimension used in GIS represents:
a. Latitude
b. Altitude
c. Magnitude
d. Longitude
View Solution
Step 1: Understanding GIS dimensions.
- GIS data is typically represented in three dimensions (3D):
- Latitude (X-axis): Represents the horizontal position.
- Longitude (Y-axis): Represents the vertical position.
- Altitude (Z-axis): Represents height or elevation above a reference surface.
Step 2: Explanation of incorrect options.
- Latitude a.: A horizontal coordinate, not a height measurement.
- Longitude d.: A vertical coordinate, not representing height.
- Magnitude c.: Refers to size or extent, not a spatial coordinate.
Step 3: Selecting the correct option.
Since the third dimension (Z-axis) in GIS represents altitude (height/elevation), the correct answer is b. Altitude. Quick Tip: In 3D GIS, the third dimension (Z-axis) represents altitude or elevation, essential for terrain modeling and analysis.
Which kind of data is mostly used in GIS?
a. Numerical data
b. Binary data
c. Spatial data
d. Boolean data
View Solution
Step 1: Understanding GIS data types.
- GIS (Geographic Information System) primarily deals with Spatial Data, which includes:
- Vector data (points, lines, polygons).
- Raster data (grids, images, elevation models).
Step 2: Explanation of incorrect options.
- Numerical data a.: Used in GIS but does not define location-based data.
- Binary data b.: Used in computing but not specific to GIS.
- Boolean data d.: Used for logical operations but not for geospatial representation.
Step 3: Selecting the correct option.
Since spatial data represents geographic locations and attributes, the correct answer is c. Spatial data. Quick Tip: GIS primarily uses Spatial Data, which includes vector (points, lines, polygons) and raster (grids, elevation models) data types.
The abbreviation of TIN is:
a. Triangulated Irregular Network
b. Temporal Information Network
c. Traffic Internet Network
d. Temperature Irregular Node
View Solution
Step 1: Understanding TIN.
- Triangulated Irregular Network (TIN) is a vector-based representation of terrain surfaces, commonly used in GIS for topographic modeling.
Step 2: Explanation of incorrect options.
- Temporal Information Network: Not related to spatial modeling.
- Traffic Internet Network: Does not exist as a GIS term.
- Temperature Irregular Node: Unrelated to GIS or terrain modeling.
Step 3: Selecting the correct option.
Since TIN is used in GIS for terrain surface modeling, the correct answer is a. Triangulated Irregular Network. Quick Tip: A Triangulated Irregular Network (TIN) represents terrain surfaces using non-overlapping triangles, ideal for 3D elevation modeling.
Which of the following is not a topological error?
a. A gap between polygons
b. Overlapped polygon
c. Unclosed polygon
d. Sliver polygon
View Solution
Step 1: Understanding topological errors in GIS.
Topological errors occur when spatial relationships between features are incorrect.
Step 2: Explanation of errors.
- Gap between polygons a.: Occurs when adjacent polygons do not meet.
- Overlapped polygon b.: Two or more polygons occupy the same area.
- Unclosed polygon c.: A polygon boundary does not connect properly.
Step 3: Explanation of sliver polygons.
- Sliver polygons d. are tiny polygons formed due to digitization errors but do not qualify as a strict topological error.
Step 4: Selecting the correct option.
Since sliver polygons are not considered major topological errors, the correct answer is d. Sliver polygon. Quick Tip: Topological errors include gaps, overlaps, and unclosed polygons, but sliver polygons are small digitization artifacts.
Which of the following scale has absolute zero?
a. Nominal Scale
b. Ratio scale
c. Interval scale
d. Ordinal scale
View Solution
Step 1: Understanding measurement scales.
- Nominal scale: Categorizes data without numerical meaning (e.g., land cover types).
- Ordinal scale: Ranks data but does not define precise differences (e.g., low, medium, high).
- Interval scale: Defines equal intervals but lacks an absolute zero (e.g., temperature in Celsius).
- Ratio scale: Defines equal intervals and has an absolute zero (e.g., height, distance).
Step 2: Selecting the correct option.
Since ratio scales have an absolute zero, the correct answer is b. Ratio scale. Quick Tip: The ratio scale allows meaningful comparisons since it has an absolute zero, unlike interval scales (e.g., temperature in Celsius).
Land cover in remote sensing corresponds to:
a. physical condition of ground surface
b. physical condition of vegetation
c. topography of the ground surface
d. soil cover on land
View Solution
Step 1: Understanding land cover in remote sensing.
- Land cover refers to the physical material covering Earth's surface, such as forests, water bodies, and urban areas.
Step 2: Explanation of incorrect options.
- Physical condition of vegetation b.: Falls under land use, not land cover.
- Topography c.: Refers to elevation, not land cover.
- Soil cover on land d.: A component of land cover but not the full definition.
Step 3: Selecting the correct option.
Since land cover refers to the physical condition of the ground surface, the correct answer is a. Physical condition of ground surface. Quick Tip: Land cover in remote sensing represents forests, urban areas, water bodies, and bare land, while land use describes human activities on land.
SAR data is suitable for assessing the:
a. health of crop
b. crop type
c. phenology of crop
d. moisture content of the crop
View Solution
Step 1: Understanding SAR data in remote sensing.
- SAR (Synthetic Aperture Radar) is a radar-based remote sensing technique that provides all-weather and day/night imaging capabilities.
- SAR is particularly sensitive to moisture content because microwave signals interact strongly with water.
Step 2: Explanation of incorrect options.
- Health of crop a.: Requires multispectral indices like NDVI, not SAR.
- Crop type b.: Determined using optical/multispectral sensors, not SAR.
- Phenology of crop c.: Based on optical imagery and time-series analysis, not SAR.
Step 3: Selecting the correct option.
Since SAR is primarily used for moisture content assessment, the correct answer is d. Moisture content of the crop. Quick Tip: SAR (Synthetic Aperture Radar) is best suited for moisture content estimation, while multispectral indices (e.g., NDVI, EVI) are used for vegetation health monitoring.
Barren rock will have NDVI of:
a. 0.1 or less
b. 0.4 or less
c. 0.1 or more
d. 0.4 or more
View Solution
Step 1: Understanding NDVI values.
- NDVI (Normalized Difference Vegetation Index) is calculated using red and near-infrared (NIR) reflectance: \[ NDVI = \frac{(NIR - Red)}{(NIR + Red)} \]
- NDVI values range from -1 to +1:
- Dense vegetation: \( 0.6 - 1.0 \)
- Sparse vegetation: \( 0.2 - 0.5 \)
- Barren surfaces (rocks, sand, urban areas): \( 0.1 \) or less
- Water bodies: Negative values
Step 2: Explanation of incorrect options.
- 0.4 or less b.: Includes areas with sparse vegetation.
- 0.1 or more c.: Includes vegetation, which is incorrect for barren rock.
- 0.4 or more d.: Represents healthy vegetation, not barren land.
Step 3: Selecting the correct option.
Since barren rock has an NDVI of 0.1 or less, the correct answer is a. 0.1 or less. Quick Tip: Barren surfaces such as rocks, deserts, and urban areas have low NDVI values (\(\leq 0.1\)), while healthy vegetation has high NDVI (\(\geq 0.6\)).
Which of the following imagery can facilitate delineation and identification of local reliefs?
a. Ortho imagery
b. Stereo imagery
c. PAN imagery
d. Geocoded imagery
View Solution
Step 1: Understanding stereo imagery.
- Stereo imagery consists of two or more images taken from different angles, allowing 3D visualization of terrain and relief features.
Step 2: Explanation of incorrect options.
- Ortho imagery a.: Provides geometrically corrected 2D images, unsuitable for relief identification.
- PAN imagery c.: High-resolution panchromatic images, but does not provide depth perception.
- Geocoded imagery d.: Has spatial reference but does not offer 3D relief details.
Step 3: Selecting the correct option.
Since stereo imagery enables 3D terrain visualization, the correct answer is b. Stereo imagery. Quick Tip: Stereo imagery is used for 3D terrain modeling, elevation mapping, and relief feature identification.
Identification and geo-location of anthropogenic features in the x-y plane is called as:
a. Anthrometry
b. Geo-anthrometry
c. Planimetry
d. Geo-planimetry
View Solution
Step 1: Understanding planimetry.
- Planimetry refers to the measurement and mapping of features in a 2D plane (x-y coordinates), without considering elevation (z-axis).
Step 2: Explanation of incorrect options.
- Anthrometry a.: Not a standard term in geospatial science.
- Geo-anthrometry b.: Incorrect term; anthropometric studies are related to human body measurements.
- Geo-planimetry d.: Not a widely used geospatial term.
Step 3: Selecting the correct option.
Since planimetry deals with mapping features in x-y coordinates, the correct answer is c. Planimetry. Quick Tip: Planimetry focuses on 2D mapping of surface features, excluding elevation or relief.
The spatial resolution of imagery recommended for assessing the damages of cultural features due to flood disaster is:
a. 20 m
b. 30 m
c. 60 m
d. 90 m
View Solution
Step 1: Understanding spatial resolution for disaster assessment.
- Higher-resolution imagery is preferred for assessing damage to cultural features.
- 30m spatial resolution (e.g., Landsat) provides sufficient detail for large-scale disaster assessment.
Step 2: Explanation of incorrect options.
- 20 m a.: Higher resolution, but 30m is more widely used.
- 60 m c. and 90 m d.: Too coarse for cultural damage assessment.
Step 3: Selecting the correct option.
Since 30m resolution (e.g., Landsat) is widely used for flood damage assessment, the correct answer is b. 30 m. Quick Tip: 30m spatial resolution (e.g., Landsat data) is commonly used for disaster assessment and damage evaluation.
Which of the following satellite data is useful for ocean monitoring?
a. Sentinel – 1A
b. Sentinel – 2B
c. Sentinel – 3
d. Sentinel – 5R
View Solution
Step 1: Understanding Sentinel missions.
- Sentinel-3 is designed for ocean monitoring, providing data on:
- Sea surface temperature
- Sea surface height
- Ocean color and currents
Step 2: Explanation of incorrect options.
- Sentinel-1A a.: Radar imaging, mainly for land applications.
- Sentinel-2B b.: Optical imaging for land vegetation monitoring.
- Sentinel-5R d.: Focused on atmospheric composition monitoring.
Step 3: Selecting the correct option.
Since Sentinel-3 is specifically designed for ocean monitoring, the correct answer is c. Sentinel – 3. Quick Tip: Sentinel-3 provides ocean monitoring data, including sea surface temperature, height, and color analysis.
Satellite remote sensor captures the sea surface temperature up to a depth of:
a. 10 micron
b. 50 micron
c. 100 micron
d. 150 micron
View Solution
Step 1: Understanding sea surface temperature (SST) measurement.
- Satellite-based remote sensors measure sea surface temperature (SST) using thermal infrared (TIR) sensors.
- These sensors detect the temperature of the uppermost thin layer of the ocean.
Step 2: Depth of SST measurement.
- Thermal infrared sensors capture the temperature of only the top 10 microns (0.01 mm) of the ocean surface.
- This is often called the "skin temperature" of the ocean.
Step 3: Explanation of incorrect options.
- 50 micron b., 100 micron c., and 150 micron d.: These depths are too deep for infrared sensors, as infrared radiation only penetrates a few microns.
Step 4: Selecting the correct option.
Since infrared sensors measure only the top 10 microns of the ocean surface, the correct answer is a. 10 micron. Quick Tip: Satellite sensors measure sea surface temperature (SST) using thermal infrared radiation, detecting the top 10 microns of the ocean surface.










Comments