Surface Areas and Volumes Important Questions

Very Short Answer Questions (1 Mark Questions)

Ques. The total surface area of a cube is 726 cm². Find the length of its edge.

Ans. Total surface area of the given cube = 726 cm²

6 × (side)² = 726

(side)² = 121

side = 11 cm

Hence, the length of the edge of the cube is calculated as 11 cm.

Ques. A cone has a height of 12 cm and a base radius of 3.5 cm, how much ice cream can be put into the cone?

Ans. radius = 3.5 cm

r = 35/10 cm

r = 7/2 cm

Height = 12 cm

Volume of cone= 1/3 × π × r² × h

= 1/3 × 22 / 7 × (7/2)² × 12

=154 cm³

Ques. Calculate what will be the edge of the cube if its volume is 1331 cm³.

Ans. Volume of cube = 1331 cm³

(Side)³ = 1331

= (11 × 11 × 11)³

Side = 11 cm

Read More: Cube Root

Ques. Find the radius of the right circular cylinder whose volume is 392π cm and height 8 cm?

Ans. Height = 8cm

volume of cylinder is πr²h

392π = πr² × 8

r² = 392 / 8

r² = 49

r = 7 cm

so radius is 7cm.

Ques. Calculate what will be the surface area of a cube whose volume is given as 216 cm³.

Ans. a³ = 216

a = 6 cm

Then, volume of a cube = a³ cu.cm and surface area = 6a² sq. cm

Surface area of given cube = 6 × 6 × 6 = 216 cm².

Ques. The surface area of a cube of side 27 cm is ________.

Ans. Surface area of cube = 6a²

= 6 × 27 × 27

= 4374 cm²

Ques. A right circular cylinder base area is 176 sq.cm and it has a radius of 4cm then find the height of the cylinder?

Ans. CSA = 176 sq. cm

radius = 4cm

CSA = 2πrh

176 = 2 × 22/7 × 4 × h

176 × 7 = 44 × 4 × h

1232 = 176 × h

h = 1232/176

h = 7cm

Therefore, the height of the right circular cylinder is 7cm.

Read More: Surface Area of Cylinder

Short Answer Questions (2 Marks Questions)

Ques. A heap of wheat is cone-shaped, whose diameter is 10.5 m and height is 3 m. Find its volume. If 1m3 wheat cost is Rs. 10, then find the total cost.

Ans. Given;

Diameter of the cone = 10.5 m

Radius of the cone (r) = 5.25 m

Height of the cone (h) = 3 m

Therefore the volume of the cone = 13πr²h

= 13 × 22/7 × 5.25 × 5.25 × 3

= 86.625 m³

Cost of 1m³ of wheat = Rs. 10

Cost of 86.625 m³ of wheat = 10 × 86.625

= Rs. 866.25

Ques. A cylindrical pipe has a length of 0.14 m and an internal radius is 0.09 m. Find the thickness of the pipe if its volume is 748.

Ans. Given that, Internal radius (r) of cylindrical pipe = 0.09 m = 9 cm

Length of cylindrical pipe (h) = 0.14 m = 14 cm

Let the external radius of the cylindrical pipe be R cm.

Volume of cylindrical pipe = 748 cm³

= π(R² – r²)h = 748

= 22/7 (R² – 92)14 = 748

=R² – 81 = (748 × 7)/(22 × 14) = 17

= R² = 81 + 17 = 98

= R = √98 = 7√2 cm = 9.9 cm

Thus, the thickness of the pipe is calculated as 9.9 – 9 = 0.9 cm

Read More: Area of Hollow Cylinder

Ques. A right-angled triangle ABC with sides of 3 cm, 4 cm, and 5 cm is revolved around the fixed side of 4 cm. find the shape of the solid generated along with the total surface area of the same?

Ans. It forms a right circular cone of radius 3 cm and height of 4 cm when the right-angled cone is rotated around a fixed side. The slant height of the cone is given as 5 cm.

Volume of cone = 1/3 πr²h

= 1/3 × 22/7 × 3 × 3 × 4 = 37.71 cm³

Total surface area of solid = πr² + πrl = πr (r + l)

=22/7 × 3 × 8 = 75.43 cm²

Ques. Calculate the surface area of a hemispherical dome of a temple with a radius of 14 m to be whitewashed from the outside.

Ans. The radius of the hemispherical dome (r) is given as 14 m

The surface area of the dome = 2πr²

= 2 × 22/7 × 14 × 14 = 1232 m²

Ques. A conical vessel has a height of 8cm and a slant height of 10cm to find the volume of the vessel.

Ans. Height of conical vessel (h) = 8 cm

Slant height of conical vessel (l) = 10 cm

∴ r² + h² = l²

⇒ r² + 8² = 10²

⇒ r² = 100 – 64 = 36

⇒ r = 6 cm

The volume of the conical vessel = 1/3πr²h = 1/3 × 22/7 × 6 × 8 = 301.71 cm³ = 0.30171 litres.

The total surface area to be whitewashed from the outside is 1232 m².

Read More: Surface Area of Right Circular Cone

Ques. A cylinder is formed with the help of a rectangular piece of paper find the volume of the cylinder to form?

Ans. Since a rectangular piece of paper is rolled along its length.

∴ 2πr = 22

r = 22/2 × 7/22 = 3.5 cm

Height of cylinder (h) = 10 cm

∴ Volume of cylinder = πr²h

= 22/7 × 3.5 × 3.5 × 10 = 385 cm³

Ques. If the numerical value of the volume is equal to the numerical value of the curved surface area, and the height of the cylinder is 5cm find the diameter of the cylinder.

Ans. Height of cylinder = 5cm

ATQ, we have

πr²h = 2πrh

r = 2 cm

Hence, diameter is 2r = 2 × 2 = 4 cm

Hence, the diameter is 4 cm.

Read More: Surface Area of a Right Circular Cylinder

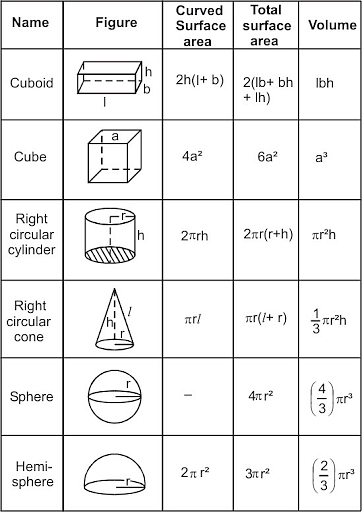
Surface Area and Volume Formulas

Long Answers Questions (3 Marks Questions)

Ques. Calculate at what speed should water flow into it an aperture of 60 cm × 45 cm so that the level of water is raised by 20 cm in 2.5 hours if the rectangular tank has base dimensions of 225 m × 162 m.

Ans. The volume of water to be flown in 2.5 hours

= 225 m × 162 m × 20 cm

= 225 × 162 × 20/100 m³

Hence water is to be flown in one hour

= 225 × 162 × 20/100 × 1 / 2.5 m³

= 2916 m³

Let the speed of flow of water in one hour be x km/hr then,

Volume of water flown in one hour = (area of aperature) × x km

=60/100 m × 45/100 m × 1000 x m

= 270 x m³

We have 270 x m³ = 2916 m³

x = 2916/279 = 10.

Read More: Area of Rectangle: Formula and Sample Questions

Ques. Each edge of a cube is increased by 50%. Calculate what will be the percentage increase in the surface area of the cube.

Ans. Let each edge of the cube by a cm.

New edge ( after increase of 50% ) = a + 50/100 a = a + a/2 = 3a/2 cm

Original surace area of cube = 6 (edges)² = 6a²

New surace area (after increase) = 6 (egdes)²

= 6(3a/2)² = 6 × 9a²/4 = 27a²/2

Total change in surface area = 27a²/2 – 6a² = 27a²/2 – 12a²/2 = 15a²/2

%increase in surface = 15a²/(2 × 6a²) × 100 = (15a² × 100) / (2 × 6a²) = 125

Hence there is 125% increase in the area of the cube.

Ques. A triangle ABC which is right-angled with dimensions of sides 5 cm, 12 cm and 13 cm is revolved around the side 5 cm. Calculate the volume of the solid so obtained. now it is revolved about the side 12 cm, then what would be the ratio of the volumes of the two solids obtained in two cases

Ans. Here, the right triangle ABC with sides of 5 cm, 12 cm, and 13 cm are revolved around the side of 5 cm.
∴ The radius of the base of the cone = 12 cm
Height of the cone = 5 cm

Hence, volume of the cone = 1/3 π (12)²(5) = π/3 × 720 cm³

Now, the right triangle ABC now revolve about the side 12 cm

The radius of the base of the cone = 5cm

Height of the cone = 12 cm

Volume of the cone = 1/3 π (5)²(12) = π/3 × 300 cm³

Now the required ratio of their volume = π/3 × 720 : π/3 × 300

Ques. A metallic circular cylinder is 15 cm in height and the diameter of the base is 14 cm. It is melted and recast into another cylinder with a radius of 14 cm. Find the height and curved surface area of the new cylinder formed after the recasting.

Ans. Height = 15 cm

Diameter = 14 cm

radius = 7cm

volume = π × r² × h = 22/7 × 49 × 15 cm³

= 22 × 7 × 15 cm³

= 2310 cm³

The radius of the new cylinder = 14 cm

let the height be h

volume = π × r² × h

= 2310 = 22/7 × 14 × 14 × h

= 2310 = 22 × 2 × 14 × h

h = 2310 / (22 × 2 × 14)

h = 3.75 cm

height = 3.75 cm

CSA = 2 × π × r × h

= 2 × 22/7 × 14 × 3.75 cm²

= 330 cm²

TSA = 2 × π × r (h + r)

= 2 × 22/7 × 14 (3.75 + 14) cm²

= 88 × 17.75 cm²

= 1562 cm²

Read More: Surface Area of a Rectangular Prism Formula

Ques. A room’s has length, breadth, and height are 5m, 4m, and 3m respectively. Find the cost of whitewashing the walls of the room and the ceiling at the rate of 7.50 per m².

Ans. Length of the room (l) = 5m

Breadth of the room (b) = 4 m

Height of the room (h) = 3 m

Since the given room is like a cuboid whose four walls (lateral surface) and ceiling are to be whitewashed.

Area to be white washed = [Lateral surface area] + [Area of the ceiling]

= [2(l + b)h] + [l × b]

= [2(5 + 4)3 m²] + [5 × 4 m²]

= [54 m²] + [20 m²] = 74 m²

Cost of white washing for 1 m² = Rs. 7.50

∴ Cost of white washing for 74 m² = Rs. 7.50 × 74

The required cost of whitewashing is Rs 555.

Ques. A semi-circular sheet of metal is of a radius of 14 cm is bent to form an open conical cup, what would be the capacity of the same?

Ans. A semicircle sheet of paper of diameter 14 cm.

The radius is R = 7 cm.

Let us consider the radius and height of the conical cup to be 'r' and 'h' respectively.

Circumference of the base of the cone = Length of the arc of the semi-circle

i.e. 2πr = ( ½) 2 π R

2r = R

2r = 7

r = 7/2

The slant height of the conical cup = Radius of the semi-circular sheet

We know that,

l² = h² + r²

(7)² = h² + (7/2)²

49 = h² + (7/2)²

49 = h² + 49/4

h² = 49 – 49/4

h² = (196 – 49)/4

h² = 167/4

h = 6.06

Height of the conical cup = 6.06 cm

V = 1/3 πr²h

V= 1/3 × 22/7 × 7/2 × 7/2 × 6.06

V= 77.77 cm³

Therefore, the capacity of the cup is calculated as 77.77 cm³.

Read More: Areas Related to Circles

Very Long Answer Questions (5 Marks Questions)

Ques. Naresh, a juice seller has set up his juice shop. He has three types of glasses (see figure) with an inner diameter of 5 cm to serve the customers. The height of the glasses is 10 cm. He decided to serve the customer in ‘A’ type of glasses. (Take π = 3.14)

(i) Find the volume of each type of glass.
(ii) Which glass has the minimum capacity?
(iii) Which mathematical concept has been implemented in the above problem?
(iv) By choosing a glass of type A, which value is depicted by juice seller Naresh?

Ans. A glass of type A:

Inner diameter = 5 cm

Inner radius = 5/2 = 2.5 cm

Height of the glass = 10 cm

The volume of a glass of type A (Since this glass has a plane bottom) = πr²h

⇒ 3.14 × 2.5 × 2.5 × 10

⇒ 196.25 cm³

Hence the volume of Glass of type A is 196.25 cm³

A glass of type B:

A glass of type B has a hemispherical raised bottom (Given)

Therefore,

The volume of glass type of B = πr²h – 2/3πr³

⇒ (3.14 × 2.5 × 2.5 × 10) – (2/3 × 3.14 × 2.5 × 2.5 × 2.5)

⇒ 196.25 – 32.71

⇒ 163.54 cm³

Hence the volume of a glass of type B is 163.54 cm³

The glass of type C:

Since the glass of type C has a conical raised bottom of the height of 1.5 cm

The volume of a glass of type C = πr²h – 1/3πr²h

⇒ (3.14 × 2.5 × 2.5 × 10) – (1/3 × 3.14 × 2.5 × 2.5 × 10)

⇒ 196.25 – 65.42

⇒ 130.83 cm³

By choosing glass A Naresh shows the value of honesty and credibility in his work. He is true to his value and has his behaviour is ethical towards his customers, as the capacity of glass A is the highest.

Ques. During one of the holiday seasons, four friends Rahul, Arun, Ajay, and Vijay went for a picnic at a hill station. However, because of the peak season, they did not get a proper Hotel in the city. They finally decided to make a conical tent at a park as the weather was quite nice. They had a 200 sq. m cloth with them with which they made the conical tent with a height of 8m and a diameter of 12m. The remaining cloth that was left was used for the floor.

1. Find the slant height of the tent.
2. How much cloth was used?
3. Find the volume of the tent
4. Find the area of the tent

Ans. conical tent with a height of 8m and diameter 12m.

=> radius = 12/2 = 6 m

h = 8 m

(1) slant height L = √(6² + 8²) = 10 m

slant height of the tent = 10 m

Lateral surface Area = πRL

= π (6) (10)

= 60π

= 60 × 3.14

= 188.4 m²

(2) cloth that was used for the floor = 200 – 188.4 = 11.6 m²

(3) The volume of the tent = (1/3) πR²h

= (1/3) (3.14) × 6² × 8

= 301.44 m³

(4) area of the floor = πR²

= 3.14 (6)²

= 113.04 m²

Read More: Surface Area Of A Hemisphere

Ques. Shreya provides water to a village, with a population of 4000, requiring 150 liters of water per head per day. She has a storage tank measuring 20 m × 15 m × 6 m. For how many days will the water in his tank last? She decreased the rate for providing water as the dependence of villagers increased on him. Which value is depicted by her?

Ans. Here, the population of the village = 4000
Requirement of water per head per day = 150 liters
∴ The total requirement of water per day = 4000 × 150 liters
= 600000 litres
The volume of the water tank = 20 × 15 × 6
= 1800 m³
= 1800 × 1000 litres
Now, the number of days for which water from the tank will last = 1800 × 1000 / 600000 = 3 days
Hence, the water tank can serve for 3 days.

Helping is necessary and is the quality possessed by her.