Collegedunia Team Content Curator
Content Curator
Rationalizing the denominator is a very important aspect in solving problems in the Real Number System. It is necessary to make the calculations simple and easier. The denominator in such numbers may contain one, two or three terms. And the method of rationalizing the denominator of such numbers varies slightly. Here we will look into how to rationalize the denominator along with some solved examples.
Read More: Angle of Depression
What is Rationalising the Denominator?
The process of converting the irrational denominator of a number to a rational number is called rationalising the denominator. This is usually done when the denominator of a number contains a term with a square root or any other number having a radical sign.
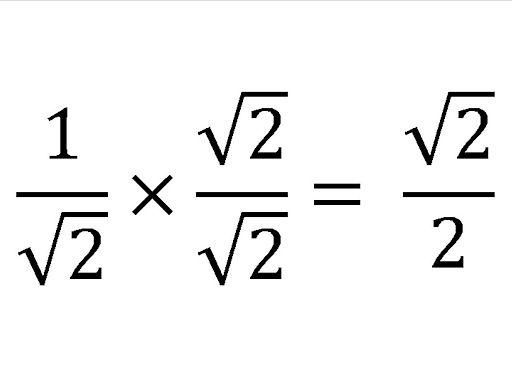
Rationalizing the Denominator
When the denominator of a number is irrational (e.g. 1/√2) it creates difficulty in performing mathematical operations. That’s why we rationalise the denominator.
Read More:
How to Rationalise the Denominator?
We usually encounter the problems of having one, two or three terms in the denominator.
Rationalising the Denominator with One Term
When the denominator has a single term (e.g. 1/√a) we multiply the numerator and denominator of that number with the denominator of that number.
To rationalise the denominator of 1/√a, we will follow the given steps:
Step 1: Observe that the denominator has only one term √a.
Step 2: We will now multiply the numerator which is 1 in this case and the denominator which is √a in this case; with √a to rationalise the denominator.
\(\frac{1}{\sqrt {a}} * \frac{\sqrt {a}}{\sqrt {a}} = \frac{\sqrt {a}} {a}\)
So, \(\frac{\sqrt {a}} {a}\) is the rationalized form of \(\frac {1}{\sqrt {a}}\)
Read More: Inverse Trigonometric Formulas
Rationalising the Denominator with Two Terms
When the denominator has two terms, we multiply the numerator and denominator of that number with the conjugate of the denominator. For example, to rationalise the denominator of 1/(√a + √b) we will multiply its numerator and denominator with the conjugate of (√a + √b), which is (√a - √b).
To rationalise the denominator of 1/(√a + √b), we will follow the given steps:
Step 1: Observe that the denominator has two terms √a + √b
Step 2: We will now multiply the numerator which is 1 in this case and the denominator with the conjugate of the denominator (√a - √b)
\(\frac {1}{\sqrt{a} + \sqrt{b}} * \frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} - \sqrt{b}}\)
Step 3: By using the algebraic formula, a2-b2 = (a+b)(a-b), we will formulate the above equation as,
\(\frac{\sqrt{a} - \sqrt{b}} {a^2 - b^2}\)
So, \(\frac{\sqrt{a} - \sqrt{b}} {a^2 - b^2}\) is the rationalized form of \(\frac {1}{\sqrt{a} + \sqrt{b}}\)
Read More:
Rationalising the Denominator with Three Terms
When the denominator has three terms, we multiply the numerator and denominator of that number with the conjugate of that number, as done in the case of the denominator with three terms. But here we need to simplify it further.
Read More:
Important Formulae
Some important identities can be useful while rationalising the denominator:
| S.no | Formula |
|---|---|
| 1. | (√a + √b)(√a - √b) = a – b, (derived from (a + b)(a – b) = a2 – b2) |
| 2. | (√a + √b)2 = a + b + 2√a×√b, (derived from (a + b)2 = a2 + b2 + 2ab) |
| 3. | (√a - √b)2 = a + b - 2√a×√b, (derived from (a - b)2 = a2 + b2 - 2ab) |
| 4. | (a + √b)(a - √b) = a2 – b |
| 5. | (√a + b)(√a - b) = a – b2 |
| 6. | (a + √b)2 = a2 + b + 2√a×b |
| 7. | (√a + b)2 = a + b2 + 2a×√b |
| 8. | (a - √b)2 = a2 + b - 2√a×b |
| 9. | (√a - b)2 = a + b2 - 2a×√b |
Things to Remember
- The process of converting the irrational denominator of a number to a rational number is called rationalising the denominator.
- This is usually done when the denominator of a number contains a term with a square root or any other number having a radical sign.
- When the denominator of a number is irrational (e.g. 1/√2) it creates difficulty in performing mathematical operations. That’s why we rationalise the denominator.
- The algebraic formula, a2-b2 = (a+b)(a-b) is important to rationalize the denominator.
Read More:
Sample Questions
Ques. Rationalise the denominator of 1/√13. (2 marks)
Ans. To rationalise the denominator of 1/√13 we’ll multiply its numerator and denominator with √13.
1/√13= 1/√13 × √13/ √13
= √13 / √13 × √13
= √13 / 13
Ques. Rationalise the denominator of 1/(10 + 2√2). (2 marks)
Ans. To rationalise the denominator of 1/(10 + 2√2) we’ll multiply its numerator and denominator with (10 - 2√2).
1/ (10+2√2) = 1/(10+2√2) × (10-2√2) / (10 - 2√2)
Using the identity: (a +√ b)(a – √b) = a2 – b2,
= 10 - 2√2 / 100 - (2√2)2
= 10 - 2√2 / 100 - 8
= 10 - 2√2 / 92
Ques. Simplify: (3 + √3)(2 + √2) (2 marks)
Ans. (3 + √3)(2 + √2)
= (3 × 2) + (3 × √2) + (√3 × 2) + (√3 × √2)
= 6 + 3√2 + 2√3 + √6
Read More:
Ques. Rationalise the denominator of 1/(√7 - √6) (2 marks)
Ans. To rationalise the denominator of 1/(√7 - √6) we’ll multiply its numerator and denominator with (√7 + √6).
1/(√7 - √6) = 1/(√7 - √6) x (√7 + √6) / (√7 + √6)
Using the identity: (√a +√b)(√a – √b) = a2 – b2,
= (√7 - √6) / 7 -6
= (√7 - √6) / 1
= (√7 - √6)
Ques. Rationalise the denominator of 1/(√7 + √5 - √2). (3 marks)
Solution. To rationalise the denominator of 1/(√7 + √5 - √2) we have to multiply its numerator and denominator with its conjugate, which we consider to be (√7 – (√5 - √2)).
1/(√7 + √5 - √2) = 1/(√7 + √5 - √2) x (√7 – (√5 - √2)) / (√7 – (√5 - √2))
Using the identity: (a + b)(a – b) = a2 – b2,
= (√7 – (√5 - √2) / (√7)2 – (√5 - √2)2
Using the identity: (a – b)2 = a2 + b2 – 2ab,
= (√7 – (√5 - √2) x 7 / (5 + 2 - 2√10)
= (√7 – (√5 - √2) x 1 / 2√10
We have to rationalise the denominator again, by multiplying the numerator and denominator with √10:
= (√7 – √5 - √2) x 1 / 2√10 x √10 / √10
= (√7 – √5 - √2) x √10 / 2 x (√10)2
= (√7 – √5 - √2) x √10 / 20
Ques. Rationalise the denominator of 5/(2√3). (2 marks)
Ans. To rationalise the denominator of 5/(2√3) we have to multiply its numerator and denominator with √3.
5/(2√3) = 5/(2√3) x √3 / √3
5/(2√3) = 5√3 / 2(√3)2
5/(2√3) = 5√3 / 6
Read More:
Ques. Rationalise the denominator of 7/(√5 + 1). (2 marks)
Ans. To rationalise the denominator of 7/(√5 + 1) we have to multiply its numerator and denominator with (√5 - 1).
7/(√5 + 1) = 7/(√5 + 1) x (√5 - 1) / (√5 - 1)
Using the identity: (a + b)(a – b) = a2 – b2,
= 7(√5 - 1)/(√5)2 - (1)2
= 7(√5 - 1)/ 5 - 1
= 7(√5 - 1) / 4
Ques. Rationalise the denominator of 1/(√5 + √3 - √2). (3 marks)
Ans. To rationalise the denominator of 1/(√5 + √3 - √2) we have to multiply its numerator and denominator with its conjugate, which we consider to be (√5 – (√3 - √2)).
1/(√5 + √3 - √2) = 1/(√5 + (√3 - √2)) x (√5 - (√3 - √2)) / (√5 - (√3 - √2))
Using the identity: (a + b)(a – b) = a2 – b2,
= (√5 - (√3 + √2)) / (√5)2 - (√3 - √2)2
Using the identity: (a – b)2 = a2 + b2 – 2ab,
= (√5 - (√3 + √2)) / 5 - (3 + 2 + 2√6)
= (√5 - (√3 + √2)) / 5 - (5 + 2√6)
= (√5 - (√3 + √2)) / 2√6
We have to rationalise the denominator again, by multiplying the numerator and denominator with √6:
(√5 - √3 + √2) / 2√6 x √6 /√6
= (√5 - √3 + √2) / 2√6 x √6 /√6
= √6 (√5 - √3 + √2) / 2 x 6
= √6 (√5 - √3 + √2) / 12
Ques. Rationalize The Denominator: 1/ √7−2 (2 marks)
Ans. The denominator can be rationalised by multiplying and dividing the fraction by the conjugate of the denominator, (√7 + 2)
i.e., by multiplying the fraction by √7+2 / √7+2
1/√7−2 = 1/√7−2 × √7+2 / √7+2
= √7+2 / (√7)2−(2)2
= √7+2 / 7−4
= √7+2 / 3
Ques. Recall, π is defined as the ratio of the circumference (c) of a circle to its diameter (d). That is, π = c/d. This seems to contradict the fact that π is irrational. How can you resolve this contradiction? (2 marks)
Ans. There is no contradiction. The measure of c will be irrational if d is rational or the measure of d will be irrational if c is rational or both c and d will be irrational. Essentially, at least one of c or d will be irrational. Because at least one of c or d is not an integer, though it is of the form c/d, π is not a rational number.
Read More:







Comments