Jasmine Grover Content Strategy Manager
Content Strategy Manager
Hexagon is a type of polygon that has basically six sides and six angles. A simple closed curve made up of line segments is called a polygon and is classified based on the number of sides. All the sides and angles in the regular polygon are equal. Hexagons can be of various types based on their properties such as Regular hexagon, Irregular Hexagon, and Concave Hexagon. A total of nine diagonals are there in a hexagon. The sum total of all the interior angles of a regular hexagon is 720 degrees, that is, each interior angle is 120 degrees. The sum of all exterior angles is 360 degrees, thus, each exterior angle is 60 degrees.
| Table of Contents |
Key Terms: Hexagon, Vertices, Faces, Area of Hexagon, Perimeter, Diagonals, Closed Curve, Polygon, Interior Angles, Exterior Angles, Regular Hexagons
Hexagon
[Click Here for Sample Questions]
A polygon is a 2D closed shape with a specific number of sides and each side is a straight line segment. A hexagon can be simply be defined as a polygon that has six sides and six angles. It is a closed curve with all the sides and angles being equal.

Hexagon
The hexagon can be classified into various types such as
- Regular hexagon
- Irregular Hexagon
- Concave Hexagon
Three are nine diagonals in a hexagon in total. The area of a Hexagon can be calculated using the formula- (3√3 s2)/ 2 while the perimeter of a hexagon is the sum of all sides.
Read More: Types of Polygon
Area of Hexagon
[Click Here for Sample Questions]
The region occupied by the two-dimensional space inside the hexagon is called the area of the hexagon. The area of a Hexagon is equal to (3√3 s2)/ 2. The area of a hexagon can also be found by dividing the hexagon into six triangles and multiplying six by the area of one such triangle.
Area of Hexagon= (3√3 s2)/ 2
Perimeter of Hexagon
[Click Here for Sample Questions]
The boundary of a hexagon is called the perimeter. Perimeter is used to find the fence of a shape for various purposes in our daily life. Perimeter is the sum of all sides of a hexagon. In a hexagon, all the sides are equal so to find the perimeter of a hexagon all you have to do is multiply the side by 6.
Perimeter of Hexagon = Sum of all Sides = 6 * side
Read More: Properties of Hexagon
Diagonals of Hexagon
[Click Here for Sample Questions]
A diagonal is termed as a straight line joining two corners. There are nine diagonal in a hexagon. The formula to find the number of diagonal in a hexagon is n (n-3)/2, where n represents the number of sides.
Diagonals of Hexagon= 6(6 – 3)/2 = 9
The formula for longer diagonal is 2s, and for shorter diagonal is √3s, where s is the side of the hexagon.
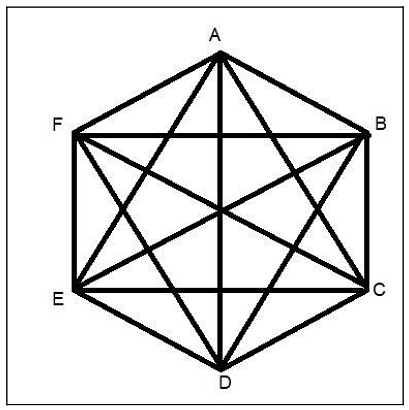
Diagonals of Hexagon
Types of Hexagon
[Click Here for Sample Questions]
The various types of a hexagon are as follows:
- Regular Hexagon: A regular hexagon is a hexagon in which all sides and angles are equal to each other.
- Irregular Hexagon: An irregular hexagon is a hexagon in which all sides and angles are not equal to each other.
- Concave Hexagon: A convex hexagon has no angles pointing inwards and no internal angles can be more than 180°.
Things to Remember
- A Polygon with six sides and six angles that are equal is known as Hexagon.
- There are various types of hexagon like Regular hexagon, Irregular Hexagon, and Concave Hexagon.
- All the sides and angles in the regular polygon are equal.
- The interior angle of a hexagon is 120 degrees and the exterior angle is 60 degrees.
- Hexagon has nine diagonals.
- Area of a Hexagon = 3√3/2 * (side)2
- The perimeter of a Hexagon= Sum of all sides = 6* side
Solved Questions
Ques. What will be the area of the hexagon whose side is 6 cm? (2 Marks)
Ans. Area of a Hexagon = 3√3/2 * (side)2
= 3√3/2 * (6)2
=3√3/2 *36
54√3 cm2.
Thus, the area of the hexagon is 54√3 cm2.
Ques. What is the measure of the side of a hexagon whose area is 24√3 cm2? (2 Marks)
Ans. Area of a Hexagon = 3√3/2 * (side)2
24√3 =3√3/2 * (side)2
16= (side)2
4 = side
The measure of the each side of the hexagon is 4 cm.
Ques. Calculate the perimeter and the area of a hexagon whose side is 7 cm. (3 Marks)
Ans. Perimeter of a Hexagon= 6* side
= 6*7
= 42 cm
As we know, Area of a Hexagon is 3√3/2 * (side)2
= 3√3/2 * (7)2
127.30573cm²
Ques. Find the cost of fencing a hexagonal field with each side of 4 cm. The cost of fencing is Rs 2 per unit. (3 Marks)
Ans. To fence a field we need to find the perimeter of the hexagon.
As we know, perimeter of a Hexagon= 6* side
= 6*4
= 24 cm
Cost of Fencing = Perimeter* Cost per unit
= 24*2
= Rs 48.
So the cost of fencing the field is Rs 48.
Ques. What will be the length of a hexagon with a perimeter of 24 units? (2 Marks)
Ans. Perimeter= 24 units
Perimeter = 6s
s= Perimeter/6
s= 24/6= 4 units
Ques. What will be the area of a hexagon with a perimeter of 12 inches? (2 Marks)
Ans. Perimeter is given as 12 inches.
P= 6s
s= P/6
s= 12/6= 2 inches.
Area of Hexagon= (3√3 s2)/ 2= (3√3 22)/ 2= 10.39 inches2
Ques. What will be the perimeter of the hexagon whose side is 5 cm? (2 Marks)
Ans. Perimeter of a Hexagon= 6* side
= 6*5
= 30 cm.
Ques. What will be the cost of mowing a hexagonal field with each side of 8 cm? The cost of mowing is Rs 2 per unit. (3 Marks)
Ans. To mow the entire field we need to find the area of the hexagon.
Area of a hexagon= 3√3/2 * (side)2
= 3√3/2 * (8)2
=3√3/2 *64
=96√3 cm2
= 166.28 cm2
The Cost of Mowing is Area * Cost per unit
= 166*2
= Rs 332.56
So the cost of fencing the field is Rs 332.56.
Ques. What is the number of diagonals that are there in a hexagon? (3 Marks)
Ans. Number of diagonals = n (n-3)/2 where n represents the number of sides in a polygon. We know that the number of sides in a hexagon is 6.
So, Number of diagonals = n (n-3)/2
= 6*3/2
= 9.
Thus, the number of diagonals in a hexagon is nine.
Ques. Find the exterior angle of a hexagon. (2 Marks)
Ans. The measure of each exterior angle = 360/n, where n represents the number of sides in a polygon. As we know that the number of sides in a hexagon is 6,
So, exterior angle = 360/6 = 60 degrees.
Ques. What will be the number of interior angles of a hexagon? (2 Marks)
Ans. Interior Angle + Exterior Angle = 180.
Interior Angle+ 60 = 180
Interior Angle = 120.
The interior angle of a hexagon is 120.
Read Also:





Comments