Arpita Srivastava Content Writer
Content Writer
In Euclidean geometry, a Kite is a quadrilateral in which two pairs of adjacent sides are of equal length. The diagonals of the figure intersect each other at right angles.
- The angles at which the pairs close to the sides meet are equal.
- It is also known as deltoids or dart.
- There are two types of kites, convex kite and concave kite.
- Convex kites have their inner angles less than 180°.
- Concave kites have at least one inner angle of more than 180°.
- The sum of the interior angles is 360 degrees.
- Its diagonals are unequal and perpendicular to each other.
- The figure has four non-collinear points.
- Sign boards and diamonds are real-life examples of Kite.
Key Terms: Kite, Right Angles, Convex Kite, Concave Kite, Quadrilateral, Angles, Triangle, Rhombus, Area of Kite, Perimeter of Kite, Diagonal of Kite, Polygon
What is a Kite?
Kite is a type of quadrilateral that has two equal angles and two pairs of adjacent equal-length sides. It is a four-sided polygon whose opposite angles are equal and congruent to each other.
- Kite has the greatest ratio of perimeter to diameter with 60°, 75°, and 150° angles.
- It forms reflection symmetry across one of its diagonals.
- Right kites resemble the shape of a cyclic quadrilateral, which consists of a circle that passes through all their vertices.
- It consists of eight polygons that can tile the plane.
- The figure has an axis of symmetry through two opposite angles.
In the quadrilateral ABCD, sides AB = BC and AD = CD. Thus, as the adjacent pairs of sides are equal, therefore ABCD is a specific type of quadrilateral known as a Kite.
- The figure shown below shows a kite:
Kite
Example of What is a Kite?Example: Find the area of a kite if its diagonals are of the length 12 units and 5 units respectively. Solution: The area of a kite can be calculated if the length of its diagonals is known.
|
Properties of Kite
[Click Here for Sample Questions]
The properties of the kite are as follows:
- A kite is a form of figure that consists of two congruent triangles having a shared base.
- Both the diagonals intersect each other at right angles.
- The smaller diagonal divides the kite into equal isosceles triangles.
- A kite is a symmetrical figure which consists of equal angles between unequal sides.
- The diagonals are bisected perpendicularly.
Proof of Properties of Kite
[Click Here for Sample Questions]
The proof of properties of kite are as follows:
Kite
Statement: The two diagonals of a Kite intersect at right angles.
Proof: From the figure above, in ΔABD and ΔBCD,
- Now, AB=BC
- And, AD=CD
- BD is common.
- Therefore ΔABD ≅ ΔBCD (by SSS rule of congruence)
- Also, in ΔABC and ΔADC
- BC = AB & CD = AD
- Thus, ΔABC is an isosceles triangle.
- ∠BAO = ∠BCO
- Thus, ΔABO ≅ ΔBCO (by ASA rule of congruence)
- ∠AOB = ∠BOC (CPCT)
- Also, ∠AOB + ∠BOC = 180° (AO & AC are Linear pair)
- ∠AOB = ∠BOC = 90
Statement: One diagonal is the perpendicular bisector of the other diagonal.
Proof: We know,
- ΔABO ≅ ΔBCO
- ∠BOC = ∠AOB = 90°
- AO = OC (Common Parts of Congruent Triangles)
- Thus, we can conclude, AC bisects BD at right angles.
Statement: Angles between unequal sides are equal.
Proof: Since, ΔBAD ≅ ΔBCD
⇒ ∠BAD = ∠BCD (Common Parts of Congruent Triangles)
Also Read:
| Related Articles | ||
|---|---|---|
| Area of Parallelogram | Quadrilateral Angle Sum Property | Differential Equation |
| First Order Differential Equation | Rolle’s Theorem | Integrals |
Area of Kite
[Click Here for Sample Questions]
The area of kite is defined as the amount of total space enclosed by a kite in a two-dimensional plane. The area is measured in terms of units2, for example, in2, cm2, m2, etc.
- The area of kite is obtained by multiplying half the length of the two diagonals.
- The area is equal to the area of the rhombus.
- To calculate the area of kite, we first need to determine the values of the diagonals.
- We can easily calculate the area of stained glass windows and diamonds.
- If the length of diagonals is given as p and q as shown in the figure given below, the area the of kite can be given as:
Area (A) = (p × q) / 2
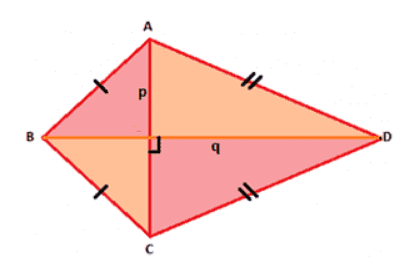
Example of Area of KiteExample: A kite has diagonals of 3 cm and 5 cm, calculate its Area. Answer: Area = (3cm x 5cm) / 2 = 7.5cm2 |
Perimeter of Kite
[Click Here for Sample Questions]
The perimeter of kite is the distance around its four sides. It is the sum of all the sides of the closed figure. It can also be calculated by adding the sides of each pair.
- The perimeter of kite is twice the sum of the length of AB and BC.
- If we look at the above figure, the four sides are AB, BC, CD & DA.
- So, the perimeter is the sum of all the sides, i.e., AB+BC+CD+DA.
- Since the adjacent sides are equal, we can say,
Perimeter (P)= 2 x (AB+BC)
Example of Perimeter of KiteExample: A kite has sides of 12 cm and 10 cm, calculate its Perimeter. Answer: Perimeter = 2 x (12cm + 10cm) = 44cm |
Diagonals of Kite
[Click Here for Sample Questions]
A kite consists of two diagonals that intersect each other at a right angle. The diagonals of the figure are not equal. The longer diagonal of the figure will divide it symmetrically.
- Longer diagonals will form two congruent triangles by the SSS property of Congruence.
- The shorter diagonal is bisected by a longer diagonal.
- Three sides of the triangle on the left of the longer diagonal are congruent to the sides of the triangle to the right.
Things to Remember
- Kite is a quadrilateral where diagonals intersect each other at right angles.
- There are two types of kites, namely, convex kite and concave kite.
- The inner angles of the convex kites are less than 180°.
- Concave kites have at least one inner angle of more than 180°.
- The sum of the interior angles of a kite is equal to 360°.
- Angles between unequal sides are equal.
Also Read:
Sample Questions
Ques. Look at the figure given below and answer the following questions: (4 marks)
(a) If AB = 7 cm, find the measure of side AC?
(b) If CD = 13 cm, find the measure of side BD?
(c) If ∠B = 118°, then find the measure of ∠C? 
Ans. (a) In the figure ABCD, AB = AC and BD = DC. Since we know that the length of AB is 7 cm, AC = 7 cm .
(b) Also, since the length of DC is 13 cm, the length of BD is also 13 cm .
(c) In the kite ABCD, ∠B = ∠C. Since the measure of ∠B is known to be 118°, ∠C is also equal to 118°.
Ques. Find the area and perimeter of a Kite where the diagonals are of length 14 cm and 16 cm respectively. (4 marks)
Ans. i) Area = (Diagonal 1 x Diagonal 2) / 2
Thus, Area = (14 cm x 16 cm) / 2
= 224 cm2 / 2
= 112 cm2
ii) Perimeter = 2 x (Diagonal 1 + Diagonal 2)
Thus, Perimeter = 2 x (14 cm + 16 cm)
= 2 x 30 cm
= 60 cm
Ques. Find the area and perimeter of the figure  given , it is given, AB = 5 cm, side BD = 26 cm, AE = 10 cm, ED = 24 cm, BE = 12 cm, EC = 12 cm. (4 marks)
given , it is given, AB = 5 cm, side BD = 26 cm, AE = 10 cm, ED = 24 cm, BE = 12 cm, EC = 12 cm. (4 marks)
Ans. The length of diagonal BC = 12 cm + 12 cm = 24 cm and the length of diagonal AD = 10 cm + 24 cm = 34 cm.
Now, Area of Kite = (length of first diagonal × length of second diagonal) / 2.
= (24 × 34) / 2
= 408 cm2.
Perimeter of Kite = Total length of all sides of the Kite.
The sides of the kite are AB, AC, BD, and DC.
From the given figure, we see that AB = 5 cm.
Therefore, from kite ABCD, AB = AC, therefore, AC is also equal to 5 cm.
As BD = 26 cm DC is also equal to 26 cm.
Therefore, sum of sides = AB + AC + BD + DC, equal to 5 + 5 + 26 + 26 = 62 cm.
Ques. Find the area and perimeter of a Kite where the diagonals are of length 24 cm and 18 cm respectively. (4 marks)
Ans. i) Area = (Diagonal 1 x Diagonal 2) / 2
Thus, Area = (24 cm x 18 cm) / 2
= 432 cm2 / 2
= 216 cm2
Thus, area of the kite is 216 cm2 .
ii) Perimeter = 2 x (Diagonal 1 + Diagonal 2)
Thus, Perimeter = 2 x (24 cm + 18 cm)
= 2 x 42 cm
= 84 cm
Thus, the perimeter of the kite is 84 cm.
Ques. The area of a Kite is 60 cm2 and the length of one of its diagonals is 12 cm. Find the length of the other diagonal. Then, find the perimeter. (4 marks)
Ans. Area of the Kite = 60 cm2
First Diagonal = 12 cm
Therefore, 60 = (12 cm x Second Diagonal) / 2
⇒ 60 = 6 x Second Diagonal
⇒ Second Diagonal = 10cm
Now, Perimeter = 2 x (12 cm + 10 cm)
= 2 X 22 cm
= 44 cm
Thus, the perimeter of the kite is 44 cm.
Ques. In a kite ABCD two pairs of adjacent sides are equal. Given that the perimeter is 56cm. Find the length of BC if side AB = 12 cm. (4 Marks)
Ans. We are given that AB = 12 and we know that AB = AD & BC = CD by property of kites.
⇒ 56 = 2 x ( BC + 12 )
⇒ 56 = 2 x BC + 24
⇒ 2BC = 56 - 24
⇒ 2BC = 32
⇒ BC = 16 cm
Ques. A kite has a 120 cm2 area and a diagonal that is 10 cm long. Determine the opposite diagonal's length. (3 marks)
Ans. Since it is given that:
- A kite's area is 120 cm2.
- One diagonal is 10 cm long.
- Area of a kite = ½ (d1 x d2)
- 120 = ½ x d1 x 10
- d2 = 12cm
Ques. Find the area of a kite if one diagonal is 14cm long, and the other diagonal is 30cm long. (2 marks)
Ans. The formula for the area of a kite is: A= ½ x d1 x d2
Plugin the values for each of the diagonals and solve.
A= ½ x 14x 30= 420/2 =210cm2
Ques. Find the perimeter of the kite whose equal sides are 30 cm and 20 cm. (2 marks)
Ans. Given a=30cm and b=20cm
Kite perimeter = 2 (a + b)
=2 (30+20)
=2 (50)
Perimeter = 100cm
Ques. A kite has its equal sides as 15 inches and 15 inches respectively. Find its perimeter. (2 marks)
Ans. Given a=15in. and b=15in.
Kite perimeter = 2 (a + b)
=2 (15+15)
=2 (30)
Perimeter = 60 inches
Ques. The sides of a kite are in the ratio of 7:6. If the side larger among them is 30 inches, find its perimeter. (4 marks)
Ans. Given: b = 40 inch
a:b = 7:6
a:30 = 7:6
a = 30 × (7/6)
b = 35 inches
Now, using the perimeter of a kite formula:
Perimeter = 2(a+b)
Perimeter = 2(30+35)
Perimeter = 2(65)
Perimeter = 130 inches
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:



Comments