Collegedunia Team Content Curator
Content Curator
Vertices, edges, and faces are the building units that make up the three-dimensional and two-dimensional structures. Mathematical shapes and structures can be in the form of two-dimensional figures, which lie on a plane surface or three-dimensional structures, which occupy space and have mass.
Key Takeaways: Shapes, Structures, Three dimensional, Two dimensional, Edges, Faces, Vertices
What is a Geometrical Shape?
Shapes form an important part of mathematics. The study of shapes in mathematics is called geometry. In geometry, a shape is defined as an enclosed structure formed by lines. These lines enclosing an area are called the boundary or outline of the shape. We are constantly surrounded by shapes in our everyday life, they can be of several types including regular, irregular, open, closed, three-dimensional, or two-dimensional.
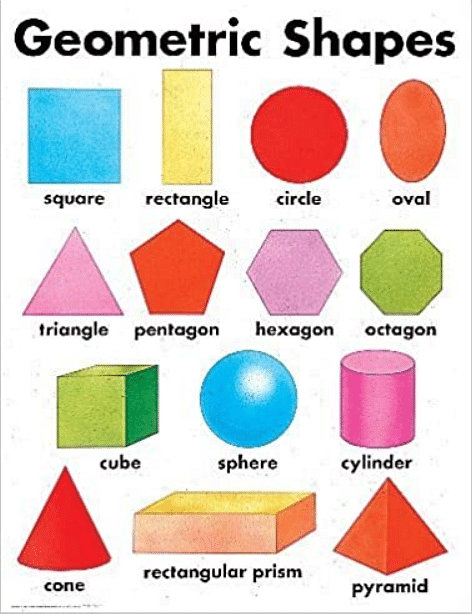
Geometric shapes
Also Read:
Types of Geometrical Shapes
The geometrical shape can be of several types as follows.
Regular shape: Has a fixed and defined shape. Eg: Sphere, circle, square, triangle, etc.
Irregular Shape: Has an undefined shape. Eg: Cloud, cotton, etc.

Irregular shapes
Open Shape: These are the shapes that are not closed and have one open side, which is an incomplete outline.
Closed Shape: They have an enclosed and complete outline defining them. Eg: Square. Triangle, cube, cuboid, etc.
Two-Dimensional Shape: They are present on a plane surface. Eg: Square, circle, triangle, rectangle, etc.
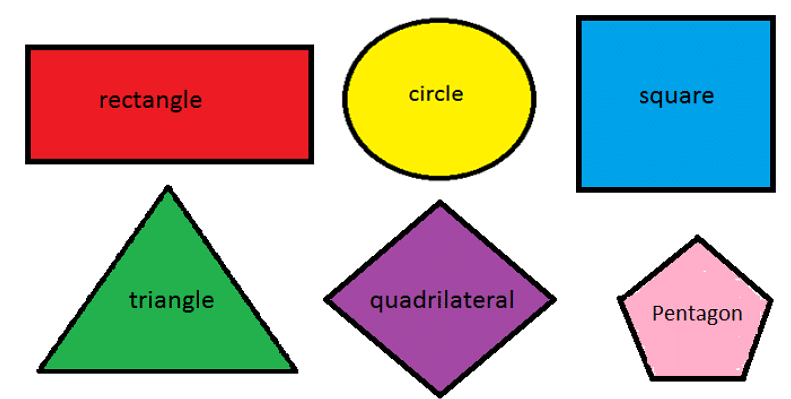
Two dimensional shape
Three-Dimensional Shape: These shapes occupy space and have mass. Eg: Cube, cuboid, prism, sphere, etc.
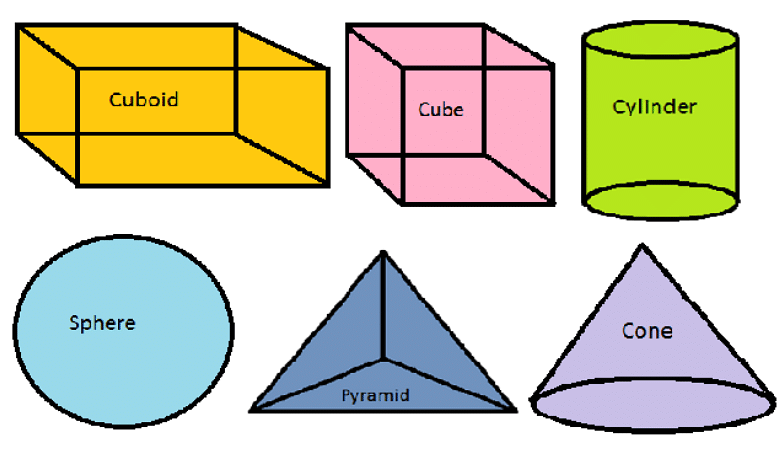
Three dimensional shape
Also Read:
Components of a mathematical structure
The regular geometric shapes are composed of three essential components which make them a defined structure. These three components are:
- Vertices
- Edges
- Faces
Vertices
A Vertice is a point where two or more than two lines join together. Also known as the corner or the tip of a structure. More than one vertex is called vertices.
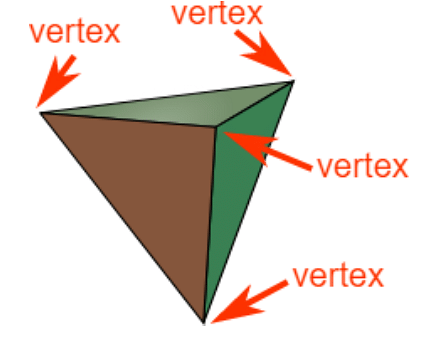
Vertices
Example:
Cube → 8 vertices
Prism → 6 vertices
Cylinder → 0 vertices
Also Read: Distance formula
Edges
An edge is a point where two or more than two faces or surfaces join together. Edge is not a point but a line segment. It provides the framework for a geometrical structure. More than one edge is called edges.
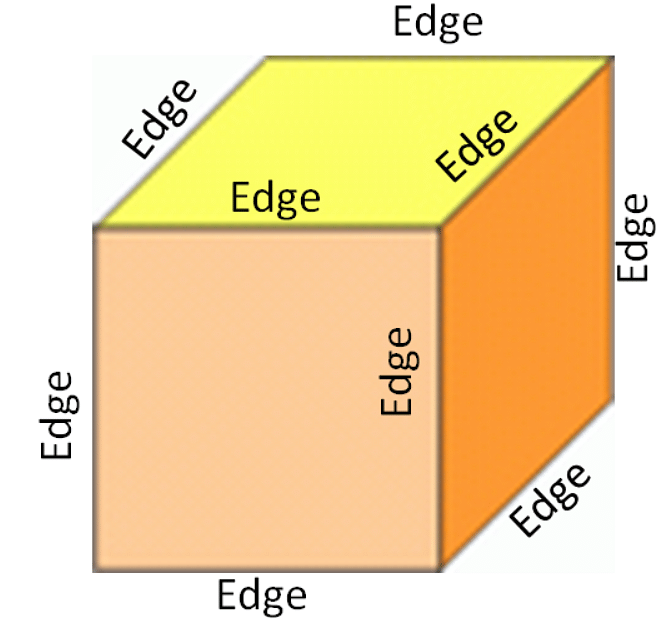
Edges
Example:
Cube → 12 edges
Prism → 9 edges
Cylinder → 3 edges
Also Read: Section Formula
Faces
The face is the flat surface of the geometrical structure. A face is like a two-dimensional shape that makes up the three-dimensional structure.
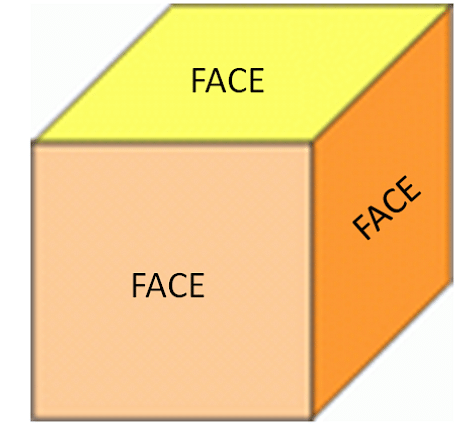
Faces
Example:
Cube → 6 faces
Prism → 5 faces
Cylinder → 3 faces
Things to Remember
- Vertices, edges, and faces are the building units that make up the three-dimensional and two-dimensional structures.
- Geometrical shapes can be of several types, regular, irregular, open, closed, three-dimensional, or two-dimensional.
- Vertice is a point where two or more than two lines join together.
- An edge is a point where two or more than two faces or surfaces join together.
- The face is the flat surface of the geometrical structure.
Also Read:
Sample Questions
Ques: What are mathematical shapes? (2 marks)
Ans: Mathematical shapes are also called geometrical shapes. A geometrical shape is defined as an enclosed structure formed by lines. These lines enclosing an area are called the boundary of the shape or its outline. A geometrical shape can be of different types, regular, irregular, open, closed, three-dimensional, or two-dimensional shapes.
Ques: Explain the different types of geometrical shapes. (5 marks)
Ans. A geometrical shape can be of different types, regular, irregular, open, closed, three-dimensional, or two-dimensional shapes.
- Regular shapes: They have a fixed and defined shape, e.g., Sphere, circle, square, triangle, etc.
- Irregular shapes: They have a non-fixed and undefined shape, ex: Cloud, cotton, etc
- Open shapes: These are the shapes that are not closed and have one open side, which is an incomplete outline.
- Closed shapes: They have an enclosed and complete outline defining them, ex: Square. Triangle, cube, cuboid, etc
- Two-dimensional shapes: They are present on a plane surface, ex: Square, circle, triangle, rectangle, etc.
- Three-dimensional shapes: These shapes occupy space and have mass, ex: cube, cuboid, prism, sphere, etc.
Ques: What are the three properties of a three-dimensional structure? (2 marks)
Ans: The regular geometric shapes are composed of three essential components which make them a defined structure. These three components are:
- Vertices: Vertice is a point where two or more than two lines join together.
- Edges: Edge is a point where two or more than two faces or surfaces join together.
- Faces: The face is the flat surface of the geometrical structure.
Ques: What is a polyhedron? (2 marks)
Ans: A polyhedron is any three-dimensional geometrical shape that has a flat face and a fixed number of edges. A polyhedron is a solid regular structure.
Also Read: Nature of Roots of Quadratic Equation
Ques: How to correlate vertices, edges, and faces? (2 marks)
Ans: The vertices, faces, and edges can be correlated in a polyhedron using Euler’s formula. According to Euler’s formula:
F + V − E = 2
F = number of faces,
V = number of vertices, and
E = number of edges.
Ques: State the number of faces, edges, and vertices of the cuboid, and what is the nature of its faces. (2 marks)
Ans: A cuboid has the following parameters:
- Faces: Six
- Edges: Twelve
- Vertices: Eight
The faces are rectangular and are two-dimensional in nature.
Ques: A polyhedron has 6 faces, and 12 edges, what are the number of vertices? (2 marks)
Ans: In order to determine the number of vertices we can use the given data and Euler’s Formula.
F + V − E = 2
F = 6
V = ?
E = 12
6+V-12=2
V-6=2
V= 8
Thus, the number of vertices is eight.
Also Read: Surface Areas and Volumes
Ques: What are the different views of a three-dimensional structure? (2 marks)
Ans: There are three types of view:
- Side view: From one side of the shape
- Top View: From the upper side of the shape
- Front view
Ques. If three cubes of dimensions 2 cm × 2 cm × 2 cm are placed end to end, what would be the dimension of the resulting cuboid? (2 marks)
Ans. Length of the resulting cuboid = 2 cm + 2 cm + 2 cm = 6 cm
Breadth = 2 cm
Height = 2 cm

Hence the required dimensions = 6 cm × 2 cm × 2 cm.
Ques. What is an edge? (2 marks)
Ans. An edge is a point where two or more than two faces or surfaces join together. Edge is not a point but a line segment. It provides the framework for a geometrical structure. More than one edge is called edges.
Example:
Cube → 12 edges
Prism → 9 edges
Cylinder → 3 edges
Also Read:




Comments