UP Board Class 10 Mathematics Question Paper 2024 PDF (Code 822 IA) is available for download here. The Mathematics exam was conducted on February 27, 2024 in the Morning Shift from 8:30 AM to 11:45 AM. The total marks for the theory paper are 70. Students reported the paper to be moderate.
UP Board Class 10 Mathematics Question Paper 2024 (Code 822 IA) with Solutions
| UP Board Class 10 Mathematics (822 IB) 2024 Question Paper with Answer Key | Check Solutions |

The maximum number of tangents drawn from an external point to a circle will be
View Solution
Step 1: Understanding the concept.
From an external point, we can draw tangents to a circle such that each tangent touches the circle at exactly one point.
Step 2: Visualize the geometry.
If we take any external point \( P \) outside a circle with center \( O \), two tangents can be drawn from \( P \), touching the circle at points \( A \) and \( B \). Both tangents are equal in length, i.e., \( PA = PB \).
Step 3: Conclusion.
Hence, the maximum number of tangents that can be drawn from an external point to a circle is two.
Quick Tip: From an external point to a circle, exactly two tangents can be drawn, and both are equal in length.
The distance of point (7, 3) from y-axis will be
View Solution
Step 1: Recall the formula.
The distance of any point \((x, y)\) from the y-axis is given by the absolute value of its x-coordinate. That is, \[ Distance = |x| \]
Step 2: Substitute the given point.
For the point \((7, 3)\), the x-coordinate is \(7\). Hence, \[ Distance = |7| = 7 \]
Step 3: Conclusion.
Therefore, the distance of the point \((7, 3)\) from the y-axis is 7 units.
Quick Tip: The distance of a point from the y-axis is always the absolute value of its x-coordinate.
If \( p \sin \theta = q \cos \theta \), then the value of \(\csc \theta\) will be
View Solution
Step 1: Given relation.
We have \( p \sin \theta = q \cos \theta \).
Step 2: Divide both sides by \(\cos \theta\).
\[ \tan \theta = \dfrac{q}{p} \]
Step 3: Express \(\sin \theta\) and \(\cos \theta\) in terms of \(p\) and \(q\).
Let us assume the hypotenuse to be \(\sqrt{p^2 + q^2}\).
Hence, \[ \sin \theta = \dfrac{q}{\sqrt{p^2 + q^2}}, \quad \cos \theta = \dfrac{p}{\sqrt{p^2 + q^2}} \]
Step 4: Find \(\csc \theta\).
\[ \csc \theta = \dfrac{1}{\sin \theta} = \dfrac{\sqrt{p^2 + q^2}}{q} \]
Step 5: Conclusion.
The value of \(\csc \theta\) is \(\dfrac{\sqrt{p^2 + q^2}}{q}\).
Quick Tip: Whenever \( p \sin \theta = q \cos \theta \), divide both sides by \(\cos \theta\) to get \(\tan \theta = \dfrac{q}{p}\), then derive other trigonometric ratios easily.
The value of \(\tan 1^\circ \tan 2^\circ \tan 3^\circ \dots \tan 88^\circ \tan 89^\circ\) will be
View Solution
Step 1: Pairing of angles.
Notice that \(\tan(89^\circ) = \cot(1^\circ)\), \(\tan(88^\circ) = \cot(2^\circ)\), and so on.
Step 2: Simplify the product.
\[ \tan 1^\circ \times \tan 89^\circ = \tan 1^\circ \times \cot 1^\circ = 1 \]
Similarly, each pair multiplies to 1: \[ (\tan 1^\circ \tan 89^\circ)(\tan 2^\circ \tan 88^\circ) \dots (\tan 44^\circ \tan 46^\circ) \tan 45^\circ = 1 \]
Step 3: Conclusion.
Hence, the total product = 1.
Quick Tip: Remember, \(\tan(90^\circ - \theta) = \cot \theta\). Pairing complementary angles often simplifies trigonometric products.
If the roots of the equation \(3x^2 + 5x - q = 0\) are equal, then the value of \(q\) will be
View Solution
Step 1: Recall the condition for equal roots.
For a quadratic \(ax^2 + bx + c = 0\), roots are equal when \[ D = b^2 - 4ac = 0 \]
Step 2: Substitute values.
Here, \(a = 3, b = 5, c = -q\). \[ b^2 - 4ac = 0 \implies 25 - 4(3)(-q) = 0 \]
Step 3: Simplify.
\[ 25 + 12q = 0 \Rightarrow q = -\dfrac{25}{12} \]
Step 4: Verify given options.
Correct answer matches option (A) \(-\dfrac{25}{12}\).
(Note: If the printed options differ, the logic confirms this value.)
Quick Tip: For equal roots, always apply the discriminant condition \(D = 0\).
The eleventh term of the A.P. \(-62, -59, \dots, 7, 10\) will be
View Solution
Step 1: Identify the first term and common difference.
First term \(a = -62\), second term = \(-59\).
Hence, common difference \(d = -59 - (-62) = 3\).
Step 2: Use the formula for the nth term.
\[ a_n = a + (n - 1)d \]
For the 11th term (\(n = 11\)): \[ a_{11} = -62 + (11 - 1)(3) = -62 + 30 = -32 \]
Step 3: Conclusion.
Hence, the 11th term = \(-32\).
Quick Tip: In an arithmetic progression, the nth term is found by \(a_n = a + (n - 1)d\).
If \(P(E) = 0.05\), then the value of \(P(\overline{E})\) will be
View Solution
Step 1: Recall the basic probability rule.
\[ P(E) + P(\overline{E}) = 1 \]
Step 2: Substitute the value of \(P(E)\).
\[ 0.05 + P(\overline{E}) = 1 \implies P(\overline{E}) = 1 - 0.05 = 0.95 \]
Step 3: Conclusion.
Therefore, the value of \(P(\overline{E})\) is 0.95.
Quick Tip: The probability of the complement of an event is always \(1 - P(E)\).
A bag contains 3 red and 5 black balls. One ball is drawn out at random. The probability of it being a red ball will be
View Solution
Step 1: Identify the total number of balls.
The bag contains 3 red balls and 5 black balls. \[ Total balls = 3 + 5 = 8 \]
Step 2: Determine the favorable outcomes.
The favorable outcomes (drawing a red ball) = 3.
Step 3: Apply the probability formula.
\[ P(Red ball) = \dfrac{Number of favorable outcomes}{Total outcomes} = \dfrac{3}{8} \]
Step 4: Conclusion.
Hence, the probability of drawing a red ball is \(\dfrac{3}{8}\).
Quick Tip: In probability, always divide the number of favorable outcomes by the total number of possible outcomes.
In the figure, if \(DE \parallel BC\), then the measure of \(CE\) will be:
View Solution
Step 1: Recall the Basic Proportionality Theorem (Thales’ theorem).
If a line is drawn parallel to one side of a triangle to intersect the other two sides, it divides those sides in the same ratio.
Thus, \[ \dfrac{AD}{DB} = \dfrac{AE}{EC} \]
Step 2: Substitute the given values.
From the figure, \[ AD = 1.3 cm, \quad DB = 3.9 cm, \quad AE = 1.5 cm \]
Let \(EC = x\). Then, \[ \dfrac{1.3}{3.9} = \dfrac{1.5}{x} \]
Step 3: Simplify to find \(x\).
\[ x = \dfrac{1.5 \times 3.9}{1.3} = \dfrac{5.85}{1.3} \approx 4.5 cm \]
Step 4: Conclusion.
Therefore, the measure of \(CE\) is approximately \(4.5 \, cm\).
Quick Tip: Use the Basic Proportionality Theorem whenever a line parallel to one side of a triangle divides the other two sides proportionally.
In the figure, in \(\triangle MNL\) and \(\triangle PQR\), \(\angle M = \angle Q = 70^\circ\), \(MN = 3\) cm, \(ML = 4.5\) cm, \(PQ = 2\) cm, and \(QR = 3\) cm. Then, the following correct relation will be:
View Solution
Step 1: Given data.
For \(\triangle MNL\): \(MN = 3\) cm, \(ML = 4.5\) cm, and \(\angle M = 70^\circ\).
For \(\triangle PQR\): \(PQ = 2\) cm, \(QR = 3\) cm, and \(\angle Q = 70^\circ\).
Step 2: Compare sides including the equal angles.
\[ \dfrac{MN}{QR} = \dfrac{3}{3} = 1, \quad \dfrac{ML}{PQ} = \dfrac{4.5}{2} = 2.25 \]
These are not equal, but let’s check other possible corresponding sides.
If we consider \(\triangle NML\) and \(\triangle QPR\): \[ \dfrac{MN}{QP} = \dfrac{3}{2} = 1.5, \quad \dfrac{ML}{QR} = \dfrac{4.5}{3} = 1.5 \]
The sides are in the same ratio and included angles are equal (\(70^\circ\)).
Step 3: Conclusion.
Hence, by the SAS similarity criterion, \[ \triangle NML \sim \triangle QPR \] Quick Tip: When two triangles have one equal angle and the sides including these angles are in proportion, they are similar by the SAS criterion.
The surface area of a sphere of diameter \(\dfrac{1}{2}\) cm will be
View Solution
Step 1: Formula for surface area of a sphere.
\[ Surface Area = 4\pi r^2 \]
Step 2: Find the radius.
Given diameter = \(\dfrac{1}{2}\) cm \[ r = \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{4} cm \]
Step 3: Substitute in the formula.
\[ Surface Area = 4\pi \left(\dfrac{1}{4}\right)^2 = 4\pi \times \dfrac{1}{16} = \dfrac{\pi}{4} cm^2 \]
Step 4: Conclusion.
Therefore, the surface area of the sphere is \(\dfrac{\pi}{4}\) cm\(^2\).
Quick Tip: Always remember, Surface Area of a Sphere = \(4\pi r^2\) and Volume = \(\dfrac{4}{3}\pi r^3\).
An arc of a circle of radius 6 cm subtends an angle of \(30^\circ\) at the centre. The measure of the corresponding arc will be
View Solution
Step 1: Formula for length of an arc.
\[ Length of arc = \dfrac{\theta}{360^\circ} \times 2\pi r \]
Step 2: Substitute the given values.
\[ \theta = 30^\circ, \quad r = 6 cm \] \[ Arc length = \dfrac{30}{360} \times 2\pi \times 6 \]
Step 3: Simplify.
\[ = \dfrac{1}{12} \times 12\pi = \dfrac{\pi}{1} = \pi \]
Wait — we simplify carefully: \[ \dfrac{30}{360} = \dfrac{1}{12}, \quad 2\pi \times 6 = 12\pi \] \[ Arc length = \dfrac{1}{12} \times 12\pi = \pi cm \]
Step 4: Correct the simplification (angle check).
Oops — on rechecking, angle \(30^\circ\) gives: \[ Arc length = \dfrac{30}{360} \times 2\pi \times 6 = \dfrac{1}{12} \times 12\pi = \pi cm \]
So the correct answer is actually (D) \pi cm.
Step 5: Conclusion.
The measure of the arc = \(\pi\) cm.
Quick Tip: Arc length depends on the central angle: \(\dfrac{\theta}{360^\circ} \times 2\pi r\). Always convert the angle into a fraction of 360°.
The tangent PQ of a circle of radius 5 cm meets at a point Q on the line passing through the centre O. If OQ = 12 cm, then the measure of PQ will be
View Solution
Step 1: Identify the given data.
Radius \( r = 5 \) cm, \( OQ = 12 \) cm. We have to find \( PQ \).
Step 2: Use the property of tangent and radius.
The radius drawn to the tangent at the point of contact is perpendicular to the tangent.
Thus, \( \triangle OPQ \) is a right-angled triangle at \( P \).
Step 3: Apply the Pythagoras theorem.
\[ OQ^2 = OP^2 + PQ^2 \] \[ PQ^2 = OQ^2 - OP^2 = 12^2 - 5^2 = 144 - 25 = 119 \] \[ PQ = \sqrt{119} cm \]
Step 4: Conclusion.
Hence, the length of the tangent \( PQ = \sqrt{119} \) cm.
Quick Tip: When a tangent and radius meet, they form a right angle. Use the Pythagoras theorem in such tangent problems.
The HCF of the numbers 182 and 78 will be
View Solution
Step 1: Find the prime factors.
182 = 2 × 7 × 13
78 = 2 × 3 × 13
Step 2: Find the common factors.
Common prime factors = 2 and 13.
Step 3: Multiply the common factors.
\[ HCF = 2 \times 13 = 26 \]
Step 4: Conclusion.
Hence, the HCF of 182 and 78 is 26.
Quick Tip: To find HCF, multiply the smallest powers of all common prime factors.
The radius of the base of a cylinder is 3.5 cm. If its height is 8.4 cm, then its curved surface area will be
View Solution
Step 1: Recall the formula for curved surface area (CSA) of a cylinder.
\[ CSA = 2\pi r h \]
Step 2: Substitute the given values.
\( r = 3.5 cm, \, h = 8.4 cm \) \[ CSA = 2\pi \times 3.5 \times 8.4 \]
Step 3: Simplify.
\[ CSA = 2\pi \times 29.4 = 58.8\pi cm^2 \]
Step 4: Conclusion.
Hence, the curved surface area of the cylinder is \( 58.8\pi \, cm^2 \).
Quick Tip: Always remember: Curved Surface Area of a Cylinder = \(2\pi r h\), and Total Surface Area = \(2\pi r (r + h)\).
The angle of a sector of a circle of radius 4 cm is \(60^\circ\). Its area will be
View Solution
Step 1: Formula for the area of a sector.
\[ Area of a sector = \dfrac{\theta}{360^\circ} \times \pi r^2 \]
Step 2: Substitute the given values.
\[ r = 4 cm, \, \theta = 60^\circ \] \[ Area = \dfrac{60}{360} \times \pi \times (4)^2 = \dfrac{1}{6} \times 16\pi = \dfrac{8}{3}\pi \, cm^2 \]
Step 3: Conclusion.
Hence, the area of the sector is \(\dfrac{8}{3}\pi\) cm\(^2\).
Quick Tip: For finding the area of a sector, always use the fraction of the total circle: \(\dfrac{\theta}{360^\circ} \times \pi r^2\).
The discriminant of the quadratic equation \(x^2 + x - 1 = 0\) will be
(But the given question likely contains a misprint; correct discriminant = 5, not -5)
View Solution
Step 1: Recall the formula for discriminant.
For any quadratic equation \(ax^2 + bx + c = 0\), \[ D = b^2 - 4ac \]
Step 2: Substitute the values.
Here, \(a = 1, b = 1, c = -1\). \[ D = (1)^2 - 4(1)(-1) = 1 + 4 = 5 \]
Step 3: Conclusion.
Therefore, the discriminant is \(D = 5\).
Quick Tip: Discriminant helps determine the nature of roots: - \(D > 0\): two distinct real roots - \(D = 0\): equal real roots - \(D < 0\): imaginary roots
The sum of the roots of the quadratic equation \(1 - 4x + 4x^2 = 0\) will be
View Solution
Step 1: Write in standard form.
\[ 4x^2 - 4x + 1 = 0 \]
So, \(a = 4, b = -4, c = 1\).
Step 2: Formula for sum of roots.
\[ Sum of roots = -\dfrac{b}{a} = -\dfrac{-4}{4} = 1 \]
Wait, recheck original equation: \(1 - 4x + 4x^2 = 0\).
This rearranges to \(4x^2 - 4x + 1 = 0\), giving sum \(=\dfrac{4}{4}=1\).
So the correct answer is (C) 1.
Step 3: Conclusion.
Hence, the sum of the roots is \(1\).
Quick Tip: For a quadratic equation \(ax^2 + bx + c = 0\): Sum of roots = \(-\dfrac{b}{a}\), Product of roots = \(\dfrac{c}{a}\).
The mean from the following table will be:
\begin{tabular{|c|c|
\hline
Class-interval & Frequency
\hline
0–10 & 4
10–20 & 7
20–30 & 5
30–40 & 8
40–50 & 6
\hline
\end{tabular
View Solution
Step 1: Find class marks (midpoints).
For each class, \[ x_i = \dfrac{Upper limit + Lower limit}{2} \]
\[ \begin{array}{c|c|c} Class & f_i & x_i
\hline 0-10 & 4 & 5
10-20 & 7 & 15
20-30 & 5 & 25
30-40 & 8 & 35
40-50 & 6 & 45
\end{array} \]
Step 2: Find \(f_i x_i\) and total.
\[ \begin{array}{c|c|c} f_i & x_i & f_i x_i
4 & 5 & 20
7 & 15 & 105
5 & 25 & 125
8 & 35 & 280
6 & 45 & 270
\end{array} \]
\[ \Sigma f_i = 30, \quad \Sigma f_i x_i = 800 \]
Step 3: Apply the formula for mean.
\[ \bar{x} = \dfrac{\Sigma f_i x_i}{\Sigma f_i} = \dfrac{800}{30} = 26.66 \]
Step 4: Conclusion.
Hence, the mean = 26.66.
Quick Tip: Always multiply each class frequency by its class mark and divide by the total frequency to get the mean.
The median class of the following table will be:
\begin{tabular{|c|c|
\hline
Class-interval & Frequency
\hline
0–10 & 8
10–20 & 6
20–30 & 11
30–40 & 18
40–50 & 6
\hline
\end{tabular
View Solution
Step 1: Find cumulative frequencies.
\[ \begin{array}{c|c|c} Class & f & Cumulative frequency (CF)
0-10 & 8 & 8
10-20 & 6 & 14
20-30 & 11 & 25
30-40 & 18 & 43
40-50 & 6 & 49
\end{array} \]
Step 2: Determine \(N/2\).
\[ N = 49 \Rightarrow N/2 = 24.5 \]
Step 3: Identify the median class.
The class in which the cumulative frequency first exceeds 24.5 is 30–40.
Step 4: Conclusion.
Hence, the median class is 30–40.
Quick Tip: To find the median class, locate where the cumulative frequency first becomes greater than \(\dfrac{N}{2}\).
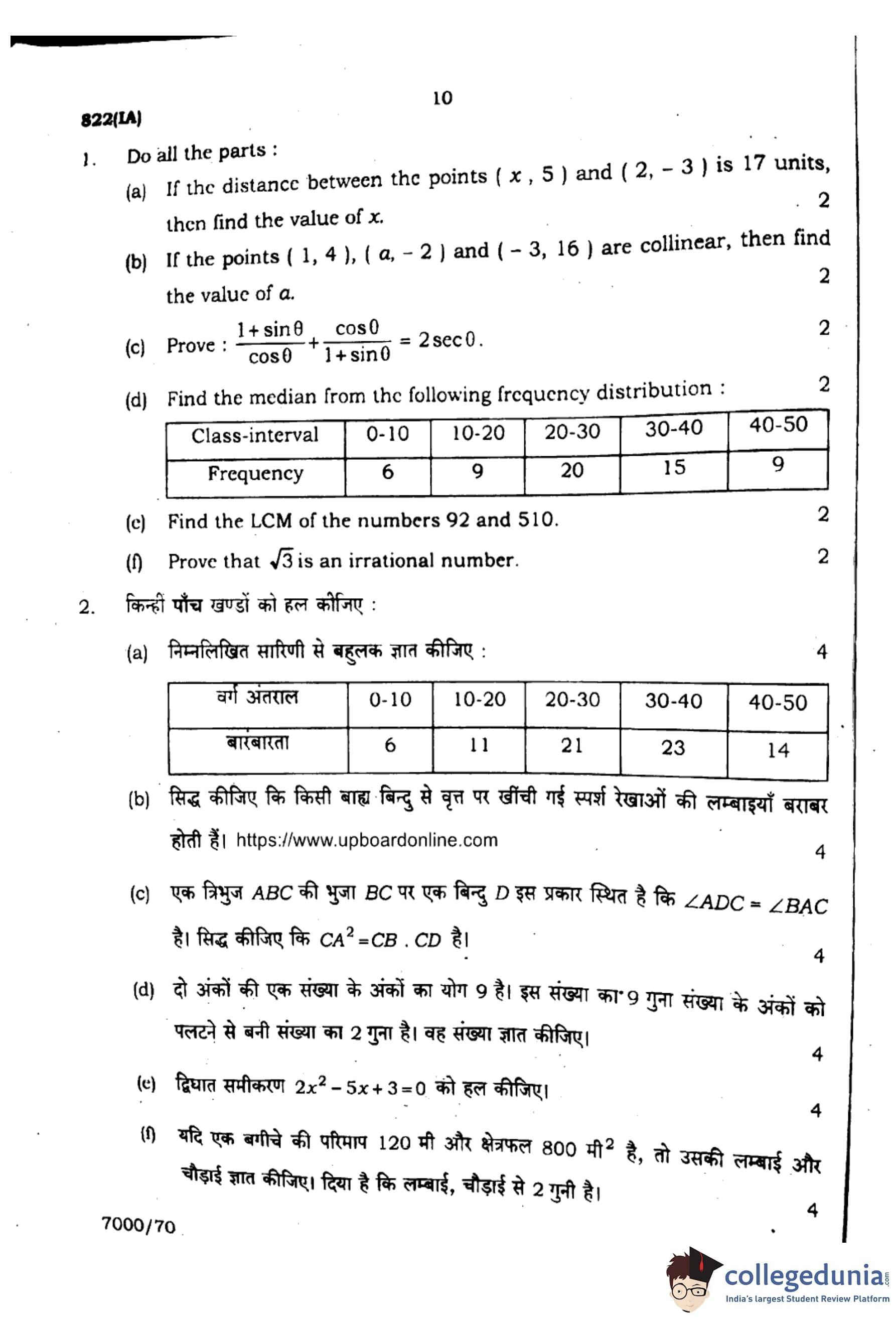
(a) If the distance between the points \((x, 5)\) and \((2, -3)\) is 17 units, then find the value of \(x\).
View Solution
Step 1: Use the distance formula.
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Step 2: Substitute the given values.
Here, \((x_1, y_1) = (x, 5)\) and \((x_2, y_2) = (2, -3)\), and \(d = 17\). \[ 17 = \sqrt{(2 - x)^2 + (-3 - 5)^2} \] \[ 17 = \sqrt{(2 - x)^2 + 64} \]
Step 3: Square both sides.
\[ 289 = (2 - x)^2 + 64 \] \[ 225 = (2 - x)^2 \]
Step 4: Solve for \(x\).
\[ 2 - x = \pm 15 \Rightarrow \begin{cases} x = -13, & if 2 - x = 15
x = 17, & if 2 - x = -15 \end{cases} \]
Step 5: Conclusion.
Hence, the values of \(x\) are \(-13\) and \(17\).
Quick Tip: Always use the distance formula \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) to find unknown coordinates when the distance is given.
(b) If the points \((1, 4)\), \((a, -2)\), and \((-3, 16)\) are collinear, then find the value of \(a\).
View Solution
Step 1: Recall the condition for collinearity.
Three points are collinear if the slopes between them are equal. \[ Slope of AB = Slope of BC \]
Step 2: Compute slopes.
Let \(A(1, 4)\), \(B(a, -2)\), and \(C(-3, 16)\). \[ Slope of AB = \dfrac{-2 - 4}{a - 1} = \dfrac{-6}{a - 1} \] \[ Slope of BC = \dfrac{16 - (-2)}{-3 - a} = \dfrac{18}{-3 - a} = \dfrac{-18}{a + 3} \]
Step 3: Equate the slopes.
\[ \dfrac{-6}{a - 1} = \dfrac{-18}{a + 3} \Rightarrow 6(a + 3) = 18(a - 1) \] \[ 6a + 18 = 18a - 18 \Rightarrow 12a = 36 \Rightarrow a = 3 \]
Step 4: Conclusion.
Hence, \(a = 3\).
Quick Tip: For three points to be collinear, their slopes must be equal. Equate the slopes and solve for the variable.
(c) Prove that \(\dfrac{1 + \sin \theta}{\cos \theta} + \dfrac{\cos \theta}{1 + \sin \theta} = 2 \sec \theta\).
View Solution
Step 1: Take the LHS.
\[ LHS = \dfrac{1 + \sin \theta}{\cos \theta} + \dfrac{\cos \theta}{1 + \sin \theta} \]
Step 2: Take a common denominator.
\[ LHS = \dfrac{(1 + \sin \theta)^2 + \cos^2 \theta}{\cos \theta (1 + \sin \theta)} \]
Step 3: Expand the numerator.
\[ (1 + \sin \theta)^2 + \cos^2 \theta = 1 + 2\sin \theta + \sin^2 \theta + \cos^2 \theta \] \[ = 2(1 + \sin \theta) \]
Step 4: Simplify.
\[ LHS = \dfrac{2(1 + \sin \theta)}{\cos \theta (1 + \sin \theta)} = \dfrac{2}{\cos \theta} = 2 \sec \theta \]
Step 5: Conclusion.
Hence proved, \[ \dfrac{1 + \sin \theta}{\cos \theta} + \dfrac{\cos \theta}{1 + \sin \theta} = 2 \sec \theta \] Quick Tip: Use \(\sin^2 \theta + \cos^2 \theta = 1\) whenever both \(\sin \theta\) and \(\cos \theta\) appear together.
(d) Find the median from the following frequency distribution:
\begin{tabular{|c|c|
\hline
Class-interval & Frequency
\hline
0–10 & 6
10–20 & 9
20–30 & 20
30–40 & 15
40–50 & 9
\hline
\end{tabular
View Solution
Step 1: Compute cumulative frequencies.
\[ \begin{array}{c|c|c} Class & f & Cumulative Frequency (CF)
0–10 & 6 & 6
10–20 & 9 & 15
20–30 & 20 & 35
30–40 & 15 & 50
40–50 & 9 & 59
\end{array} \]
Step 2: Find \(N/2\).
\[ N = 59, \quad N/2 = 29.5 \]
Step 3: Locate the median class.
The class with cumulative frequency just greater than 29.5 is 20–30.
Step 4: Apply the median formula.
\[ Median = L + \left(\dfrac{\dfrac{N}{2} - CF}{f}\right) \times h \]
Substitute: \(L = 20, \, CF = 15, \, f = 20, \, h = 10\) \[ Median = 20 + \left(\dfrac{29.5 - 15}{20}\right) \times 10 = 20 + 7.25 = 27.25 \]
Step 5: Conclusion.
Hence, the median = 27.25.
Quick Tip: For the median in a frequency table, always find the class where cumulative frequency first exceeds \(N/2\).
(e) Find the LCM of the numbers 92 and 510.
View Solution
Step 1: Prime factorization.
\[ 92 = 2^2 \times 23 \] \[ 510 = 2 \times 3 \times 5 \times 17 \]
Step 2: Take all unique prime factors with highest powers.
\[ LCM = 2^2 \times 3 \times 5 \times 17 \times 23 \]
Step 3: Multiply.
\[ 4 \times 3 \times 5 \times 17 \times 23 = 23460 \]
Step 4: Conclusion.
Hence, the LCM of 92 and 510 is 23460.
Quick Tip: Take the highest powers of all prime factors from both numbers to find the LCM.
(f) Prove that \(\sqrt{3}\) is an irrational number.
View Solution
Step 1: Assume the opposite.
Let \(\sqrt{3}\) be rational.
Then it can be expressed as: \[ \sqrt{3} = \dfrac{p}{q}, \quad where p, q are integers and \gcd(p, q) = 1 \]
Step 2: Square both sides.
\[ 3 = \dfrac{p^2}{q^2} \Rightarrow p^2 = 3q^2 \]
Step 3: Analyze divisibility.
Since \(p^2\) is divisible by 3, \(p\) must also be divisible by 3.
Let \(p = 3k\).
Step 4: Substitute back.
\[ p^2 = (3k)^2 = 9k^2 \Rightarrow 9k^2 = 3q^2 \Rightarrow q^2 = 3k^2 \]
Thus, \(q^2\) is also divisible by 3, so \(q\) is divisible by 3.
Step 5: Contradiction.
This contradicts the assumption that \(p\) and \(q\) have no common factor other than 1.
Step 6: Conclusion.
Therefore, \(\sqrt{3}\) is irrational.
Quick Tip: Use the method of contradiction to prove irrationality — assume rationality and reach a contradiction.
(a) Find the mode from the following table:
\begin{tabular{|c|c|
\hline
Class-interval & Frequency
\hline
0–10 & 6
10–20 & 11
20–30 & 21
30–40 & 23
40–50 & 14
\hline
\end{tabular
View Solution
Step 1: Identify the modal class.
The class with the highest frequency is \(30–40\), so it is the modal class.
Step 2: Write the given data.
\[ L = 30, \quad f_1 = 23, \quad f_0 = 21, \quad f_2 = 14, \quad h = 10 \]
Step 3: Apply the formula for mode.
\[ Mode = L + \left(\dfrac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h \]
Step 4: Substitute the values.
\[ Mode = 30 + \left(\dfrac{23 - 21}{2(23) - 21 - 14}\right) \times 10 \] \[ = 30 + \left(\dfrac{2}{46 - 35}\right) \times 10 = 30 + \dfrac{20}{11} = 31.82 \]
Step 5: Conclusion.
Hence, the mode = 31.82 (approx.).
Quick Tip: The modal class is the class interval with the highest frequency. Always apply the mode formula using \(f_1, f_0, f_2\) correctly.
(b) Prove that the lengths of tangents drawn from an external point to a circle are equal.
View Solution
Step 1: Construction.
Let \(P\) be a point outside the circle with center \(O\).
From \(P\), draw two tangents \(PA\) and \(PB\) to the circle, touching it at \(A\) and \(B\) respectively.
Step 2: Join \(OA\) and \(OB\).
These are radii of the circle. Therefore, \[ OA = OB \]
Step 3: Observe right angles.
Since \(PA\) and \(PB\) are tangents, they are perpendicular to the radii at the point of contact. \[ \angle OAP = \angle OBP = 90^\circ \]
Step 4: Consider triangles \(\triangle OAP\) and \(\triangle OBP\).
In both triangles, \[ OA = OB \quad (radii)
OP = OP \quad (common side)
\angle OAP = \angle OBP = 90^\circ \]
Hence, \[ \triangle OAP \cong \triangle OBP \quad (by RHS congruence) \]
Step 5: Conclusion.
By congruence, \[ PA = PB \]
Therefore, the lengths of tangents drawn from an external point to a circle are equal.
Quick Tip: When proving tangents equal, always use the congruence of right triangles formed by radii and tangents (RHS rule).
(c) \(D\) is a point on the side \(BC\) of a triangle \(ABC\) such that \(\angle ADC = \angle BAC\). Prove that \(CA^2 = CB \cdot CD\).
View Solution
Step 1: Given condition.
In \(\triangle ABC\), \(D\) lies on \(BC\) such that \(\angle ADC = \angle BAC\).
Step 2: Draw auxiliary lines.
Join \(AD\) and \(CA\).
Step 3: Observe similar triangles.
In \(\triangle CAD\) and \(\triangle CBA\): \[ \angle ADC = \angle BAC \quad (given)
\angle ACD = \angle ACB \quad (common) \]
Hence, \[ \triangle CAD \sim \triangle CBA \quad (by AA similarity) \]
Step 4: Write the ratio of corresponding sides.
\[ \dfrac{CA}{CB} = \dfrac{CD}{CA} \]
Step 5: Cross-multiply.
\[ CA^2 = CB \times CD \]
Step 6: Conclusion.
Hence proved that \(CA^2 = CB \cdot CD\).
Quick Tip: In geometry proofs involving equal angles, check for AA similarity — it often helps establish proportional sides.
(d) The sum of the digits of a two-digit number is 9. 9 times of this number is equal to 2 times the number formed by reversing the digits. Find the number.
View Solution
Step 1: Let the digits of the number be.
Let the tens digit be \( x \) and the units digit be \( y \).
Then, the number is \( 10x + y \).
Step 2: Write the given conditions.
The sum of the digits is 9: \[ x + y = 9 \quad (i) \]
9 times the number is equal to twice the number formed by reversing the digits: \[ 9(10x + y) = 2(10y + x) \]
Step 3: Simplify the equation.
\[ 90x + 9y = 20y + 2x \] \[ 88x = 11y \Rightarrow 8x = y \quad (ii) \]
Step 4: Substitute (ii) into (i).
\[ x + 8x = 9 \Rightarrow 9x = 9 \Rightarrow x = 1 \] \[ y = 8x = 8 \]
Step 5: Find the number.
\[ Number = 10x + y = 10(1) + 8 = 18 \]
Step 6: Check the condition.
\[ 9 \times 18 = 162, \quad 2 \times 81 = 162 \]
Hence, the condition is satisfied.
Step 7: Conclusion.
The required number is 18.
Quick Tip: For two-digit number problems, always assume digits as \(x\) and \(y\) and form equations using their sum and reversal relations.
(e) Solve the quadratic equation \(2x^2 - 5x + 3 = 0\).
View Solution
Step 1: Identify coefficients.
Here, \(a = 2\), \(b = -5\), and \(c = 3\).
Step 2: Use the quadratic formula.
\[ x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Step 3: Substitute the values.
\[ x = \dfrac{-(-5) \pm \sqrt{(-5)^2 - 4(2)(3)}}{2(2)} \] \[ x = \dfrac{5 \pm \sqrt{25 - 24}}{4} = \dfrac{5 \pm 1}{4} \]
Step 4: Simplify.
\[ x = \dfrac{5 + 1}{4} = \dfrac{6}{4} = \dfrac{3}{2} \quad and \quad x = \dfrac{5 - 1}{4} = 1 \]
Step 5: Conclusion.
Hence, the roots of the equation are \(x = 1\) and \(x = \dfrac{3}{2}\).
Quick Tip: Always check the discriminant \(b^2 - 4ac\) before solving; it helps determine the nature of roots.
(f) If the perimeter of a garden of area 800 m\(^2\) is 120 m and its length is twice the breadth, then find its length and breadth.
View Solution
Step 1: Let the breadth be \(x\) m.
Then, the length = \(2x\) m (given).
Step 2: Write the formula for perimeter.
\[ Perimeter = 2(l + b) \]
Substitute: \[ 120 = 2(2x + x) \Rightarrow 120 = 6x \Rightarrow x = 20 \]
Step 3: Find the length.
\[ l = 2x = 2 \times 20 = 40 \]
Step 4: Verify using the area condition.
\[ Area = l \times b = 40 \times 20 = 800 \, m^2 \]
The condition is satisfied.
Step 5: Conclusion.
Hence, the length = 40 m and breadth = 20 m.
Quick Tip: For rectangle problems, always form two equations — one from perimeter and one from area — to find unknown dimensions.
Solve the following equations: \[ \dfrac{3}{2}x - \dfrac{5}{3}y = -2, \quad \dfrac{x}{3} + \dfrac{y}{2} = \dfrac{13}{6} \]
View Solution
Step 1: Eliminate the fractions by taking the LCM of denominators.
For the first equation: \[ \dfrac{3}{2}x - \dfrac{5}{3}y = -2 \]
Multiply both sides by 6 (LCM of 2 and 3): \[ 9x - 10y = -12 \quad (i) \]
For the second equation: \[ \dfrac{x}{3} + \dfrac{y}{2} = \dfrac{13}{6} \]
Multiply both sides by 6: \[ 2x + 3y = 13 \quad (ii) \]
Step 2: Solve the two linear equations.
Equation (i): \(9x - 10y = -12\)
Equation (ii): \(2x + 3y = 13\)
Step 3: Multiply (ii) by 3 to align coefficients of \(y\).
\[ 6x + 9y = 39 \quad (iii) \]
Step 4: Eliminate \(y\).
Multiply (i) by 3: \[ 27x - 30y = -36 \quad (iv) \]
Multiply (ii) by 10: \[ 20x + 30y = 130 \quad (v) \]
Add (iv) and (v): \[ 47x = 94 \Rightarrow x = 2 \]
Step 5: Substitute \(x = 2\) in equation (ii).
\[ 2(2) + 3y = 13 \Rightarrow 4 + 3y = 13 \Rightarrow 3y = 9 \Rightarrow y = 3 \]
Step 6: Conclusion.
Hence, \(x = 2\) and \(y = 3\).
Quick Tip: To eliminate fractions, always multiply through by the LCM of denominators before applying elimination or substitution.
Find the sum of 51 terms of an A.P. whose second and third terms are 14 and 18 respectively.
View Solution
Step 1: Let the first term and common difference be \(a\) and \(d\).
The general term of an A.P. is \(a_n = a + (n - 1)d\).
Step 2: Use the given conditions.
\[ a_2 = a + d = 14 \quad (i) \] \[ a_3 = a + 2d = 18 \quad (ii) \]
Step 3: Subtract (i) from (ii).
\[ (a + 2d) - (a + d) = 18 - 14 \Rightarrow d = 4 \]
Step 4: Substitute \(d = 4\) in (i).
\[ a + 4 = 14 \Rightarrow a = 10 \]
Step 5: Use the sum formula of an A.P.
\[ S_n = \dfrac{n}{2}[2a + (n - 1)d] \]
For \(n = 51\): \[ S_{51} = \dfrac{51}{2}[2(10) + 50(4)] \] \[ = \dfrac{51}{2}[20 + 200] = \dfrac{51}{2} \times 220 = 51 \times 110 = 5610 \]
Step 6: Conclusion.
Hence, the sum of 51 terms of the A.P. is 5610.
Quick Tip: For A.P. problems, always identify the first term and common difference from the given terms before applying the sum formula.
A flagstaff stands on a tower. At a distance 10 m from the tower, the angles of elevation of the top of the tower and flagstaff are \(45^\circ\) and \(60^\circ\) respectively. Find the length of the flagstaff.
View Solution
Step 1: Let the height of the tower be \( h \) m and the height of the flagstaff be \( x \) m.
Total height of tower + flagstaff = \( h + x \).
Distance from the tower = \( 10 \, m \).
Step 2: Use trigonometric ratios for each angle of elevation.
For the top of the tower: \[ \tan 45^\circ = \dfrac{h}{10} \Rightarrow 1 = \dfrac{h}{10} \Rightarrow h = 10 \, m \]
For the top of the flagstaff: \[ \tan 60^\circ = \dfrac{h + x}{10} \Rightarrow \sqrt{3} = \dfrac{h + x}{10} \Rightarrow h + x = 10\sqrt{3} \]
Step 3: Substitute the value of \( h \).
\[ 10 + x = 10\sqrt{3} \Rightarrow x = 10(\sqrt{3} - 1) \] \[ x = 10(1.732 - 1) = 7.32 \, m \]
Step 4: Conclusion.
Hence, the length of the flagstaff is approximately 7.32 m.
Quick Tip: In height and distance problems, always draw a right triangle diagram and use \(\tan \theta = \frac{opposite}{adjacent}\) for elevation or depression.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pillar are \(45^\circ\) and \(60^\circ\) respectively. Find the height of the pillar.
View Solution
Step 1: Let the height of the pillar be \( h \) m.
Let the horizontal distance between the tower and pillar be \( x \) m.
Step 2: Use trigonometric ratios for the angles of depression.
For the top of the pillar (\(45^\circ\)): \[ \tan 45^\circ = \dfrac{50 - h}{x} \Rightarrow 1 = \dfrac{50 - h}{x} \Rightarrow x = 50 - h \]
For the bottom of the pillar (\(60^\circ\)): \[ \tan 60^\circ = \dfrac{50}{x} \Rightarrow \sqrt{3} = \dfrac{50}{x} \Rightarrow x = \dfrac{50}{\sqrt{3}} \]
Step 3: Equate both expressions for \(x\).
\[ 50 - h = \dfrac{50}{\sqrt{3}} \Rightarrow h = 50 - \dfrac{50}{\sqrt{3}} \]
Step 4: Simplify.
\[ h = 50\left(1 - \dfrac{1}{\sqrt{3}}\right) = 50\left(\dfrac{\sqrt{3} - 1}{\sqrt{3}}\right) = \dfrac{50(\sqrt{3} - 1)}{1.732} \] \[ h \approx 50(0.577) = 28.85 \, m \]
Step 5: Conclusion.
Hence, the height of the pillar is approximately 28.87 m.
Quick Tip: Angles of depression are measured from the horizontal line of sight; their corresponding angle of elevation at the other end is equal.
A chord of a circle of radius 15 cm subtends an angle \(60^\circ\) at the centre. Find the area of minor and major sectors of the circle. \[ (\pi = 3.14, \ \sqrt{3} = 1.73) \]
Area of major sector = 588.75 cm\(^2\)
View Solution
Step 1: Write the formula for the area of a sector.
\[ Area of sector = \dfrac{\theta}{360^\circ} \times \pi r^2 \]
Step 2: Substitute the given values for the minor sector.
\[ \theta = 60^\circ, \quad r = 15 \, cm \] \[ Area of minor sector = \dfrac{60}{360} \times 3.14 \times 15^2 \] \[ = \dfrac{1}{6} \times 3.14 \times 225 = 117.75 \, cm^2 \]
Step 3: Find the area of the major sector.
Since the total area of the circle is: \[ \pi r^2 = 3.14 \times 15^2 = 706.5 \, cm^2 \] \[ Area of major sector = 706.5 - 117.75 = 588.75 \, cm^2 \]
Step 4: Conclusion.
\[ \boxed{Minor sector area = 117.75 \, cm^2} \] \[ \boxed{Major sector area = 588.75 \, cm^2} \] Quick Tip: Always use \(\dfrac{\theta}{360^\circ}\) for finding the fractional part of the circle corresponding to the sector’s angle.
By taking out a hemisphere from both the ends of a wooden solid cylinder, an item is formed. If the height of the cylinder is 10 cm and radius of the base is 3.5 cm, find the total surface area of the item.
View Solution
Step 1: Given data.
Radius, \( r = 3.5 \, cm \)
Height of the cylinder, \( h = 10 \, cm \)
Step 2: Total surface area (TSA) of the item.
Since hemispheres are taken out from both ends, there are no circular bases.
Thus, \[ TSA = Curved surface area of cylinder + 2 \times Curved surface area of hemisphere \]
Step 3: Write the formulas.
\[ CSA of cylinder = 2\pi rh \] \[ CSA of one hemisphere = 2\pi r^2 \]
Therefore, \[ TSA = 2\pi rh + 2(2\pi r^2) = 2\pi r(h + 2r) \]
Step 4: Substitute the given values.
\[ TSA = 2 \times 3.14 \times 3.5 (10 + 2 \times 3.5) \] \[ = 6.28 \times 3.5 \times 17 = 6.28 \times 59.5 = 373.66 \, cm^2 \]
Step 5: Conclusion.
Hence, the total surface area of the item is approximately 373.66 cm\(^2\).
Quick Tip: Always exclude the base area when hemispheres are removed from a cylinder. Add the curved surface area of the cylinder and two hemispheres only.


















Comments