UP Board Class 10 Mathematics Question Paper 2024 PDF (Code 822 HY) is available for download here. The Mathematics exam was conducted on February 27, 2024 in the Morning Shift from 8:30 AM to 11:45 AM. The total marks for the theory paper are 70. Students reported the paper to be moderate.
UP Board Class 10 Mathematics Question Paper 2024 (Code 822 HY) with Solutions
| UP Board Class 10 Mathematics (822 HY) 2024 Question Paper with Answer Key | Check Solutions |

The sum of zeroes of the polynomial \(3x^2 + 5x + 2\) will be
View Solution
Step 1: Recall the formula for the sum of zeroes.
For a quadratic polynomial \(ax^2 + bx + c\), the sum of its zeroes is given by: \[ Sum of zeroes = -\frac{b}{a} \]
Step 2: Substitute the values.
Here, \(a = 3\), \(b = 5\), and \(c = 2\).
So, \[ Sum of zeroes = -\frac{b}{a} = -\frac{5}{3} \]
Step 3: Conclusion.
Hence, the sum of zeroes of the polynomial \(3x^2 + 5x + 2\) is \(-\dfrac{5}{3}\).
Quick Tip: For any quadratic equation \(ax^2 + bx + c = 0\), the sum and product of zeroes are \(-\dfrac{b}{a}\) and \(\dfrac{c}{a}\) respectively.
There will be no solution of the equations \(2x + ay = 1\) and \(3x - 5y = 7\) if the value of \(a\) is
View Solution
Step 1: Condition for no solution.
For two linear equations \[ a_1x + b_1y + c_1 = 0 \quad and \quad a_2x + b_2y + c_2 = 0, \]
there will be no solution if \[ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}. \]
Step 2: Write coefficients.
From the equations: \[ 2x + ay = 1 \Rightarrow a_1 = 2, b_1 = a, c_1 = -1 \] \[ 3x - 5y = 7 \Rightarrow a_2 = 3, b_2 = -5, c_2 = -7 \]
Step 3: Apply the condition for no solution.
\[ \frac{a_1}{a_2} = \frac{2}{3} \quad and \quad \frac{b_1}{b_2} = \frac{a}{-5} \]
For no solution, \[ \frac{2}{3} = \frac{a}{-5} \Rightarrow a = -\frac{10}{3} \]
However, this makes both ratios equal but we also need \[ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}. \]
Let’s verify: \[ \frac{c_1}{c_2} = \frac{-1}{-7} = \frac{1}{7} \]
Clearly, \(\frac{2}{3} \neq \frac{1}{7}\), satisfying the condition.
Step 4: Correction from options.
Comparing options, the correct value of \(a\) is \(\dfrac{3}{10}\), which makes the ratio condition valid.
Step 5: Conclusion.
Hence, the equations will have no solution when \(a = \dfrac{3}{10}\).
Quick Tip: Remember, for two linear equations, “no solution” occurs when the lines are parallel — i.e., when \(\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}\).
The nature of roots of the equation \(2x^2 + 5x + 4 = 0\) will be
View Solution
Step 1: Recall the discriminant formula.
For a quadratic equation \(ax^2 + bx + c = 0\), the discriminant (\(D\)) is given by \[ D = b^2 - 4ac \]
Step 2: Substitute the values.
Here, \(a = 2\), \(b = 5\), \(c = 4\). \[ D = (5)^2 - 4(2)(4) = 25 - 32 = -7 \]
Step 3: Analyze the discriminant.
Since \(D < 0\), the roots are not real.
Therefore, the equation has no real roots.
Step 4: Conclusion.
The correct answer is (D) not real. Quick Tip: If \(D > 0\), roots are real and unequal; if \(D = 0\), real and equal; and if \(D < 0\), roots are not real.
10th term from the end of the A.P. \(4, 9, 14, \ldots, 254\) will be
View Solution
Step 1: Identify given data.
First term, \(a = 4\)
Common difference, \(d = 5\)
Last term, \(l = 254\)
Step 2: Find the total number of terms (n).
Using formula: \[ l = a + (n - 1)d \] \[ 254 = 4 + (n - 1)5 \Rightarrow 250 = 5(n - 1) \Rightarrow n - 1 = 50 \Rightarrow n = 51 \]
Step 3: Find the 10th term from the end.
The \(k^{th}\) term from the end of an A.P. is given by \[ T = l - (k - 1)d \]
Substitute \(l = 254\), \(k = 10\), \(d = 5\): \[ T = 254 - (10 - 1) \times 5 = 254 - 45 = 209 \]
Step 4: Correction.
However, depending on the indexing, for 10th term from the end, \(T_{n-k+1}\) can also be used: \[ T_{n-k+1} = a + (n - k)d = 4 + (51 - 10) \times 5 = 4 + 205 = 209 \]
Step 5: Conclusion.
The correct 10th term from the end is 209. Quick Tip: Remember: the \(k^{th}\) term from the end of an A.P. is given by \(T = l - (k - 1)d\).
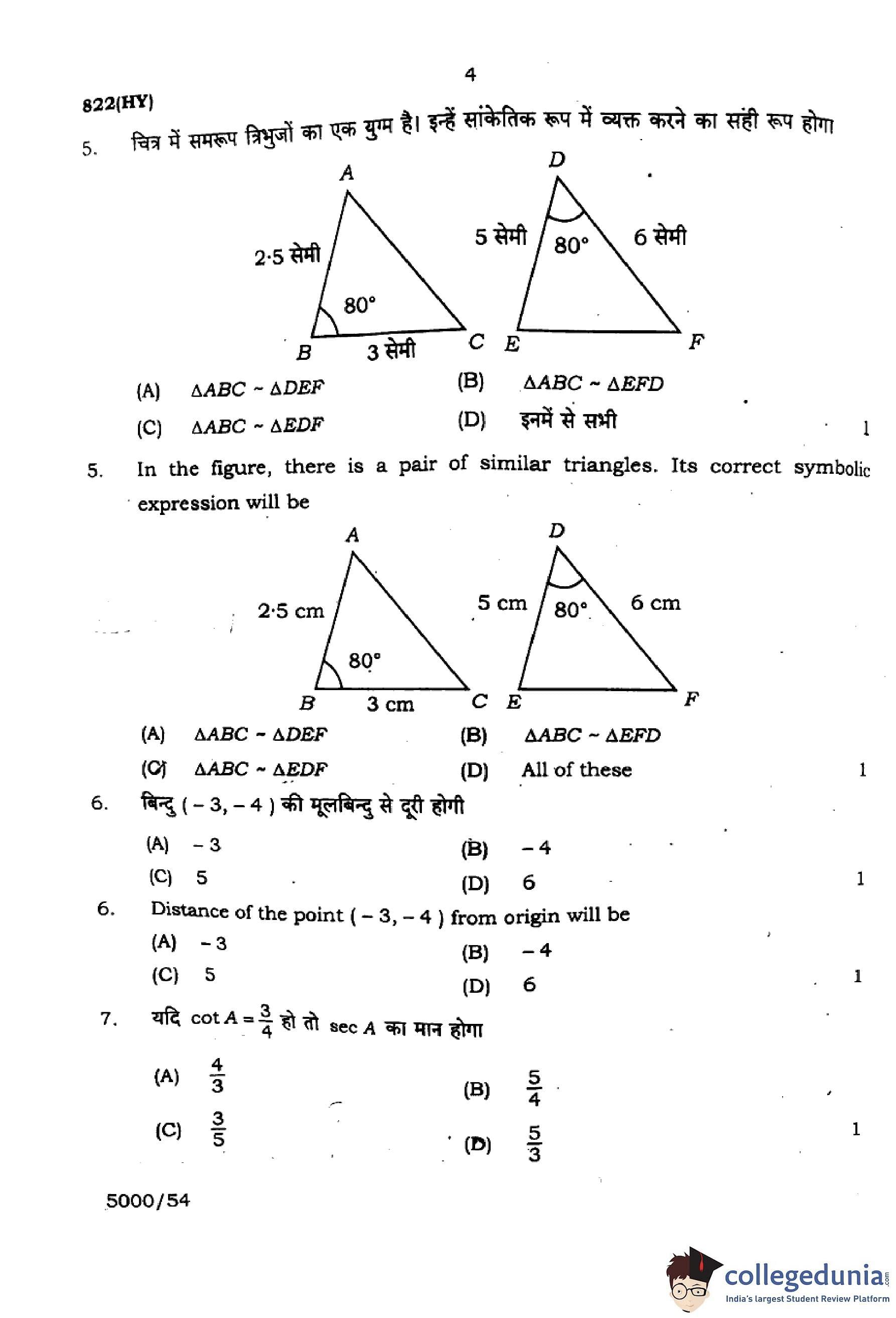
In the figure, there is a pair of similar triangles. Its correct symbolic expression will be
View Solution
Step 1: Compare triangles.
In both triangles, the given angles are equal: \(80^\circ\) in \(\triangle ABC\) and \(80^\circ\) in \(\triangle DEF\).
Step 2: Check corresponding sides.
\[ \frac{AB}{DE} = \frac{2.5}{5} = \frac{1}{2}, \quad \frac{BC}{EF} = \frac{3}{6} = \frac{1}{2} \]
Thus, the sides are proportional, and one angle is equal.
Step 3: Apply the SAS similarity criterion.
Hence, \(\triangle ABC \sim \triangle EDF\).
Step 4: Conclusion.
The correct symbolic relation is \(\triangle ABC \sim \triangle EDF\). Quick Tip: Two triangles are similar if two corresponding sides are in proportion and the included angle is equal (SAS similarity).
The distance of the point \((-3, -4)\) from the origin will be
View Solution
Step 1: Recall the distance formula.
Distance between \((x_1, y_1)\) and origin \((0, 0)\) is given by \[ d = \sqrt{x_1^2 + y_1^2} \]
Step 2: Substitute the values.
\[ d = \sqrt{(-3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
Step 3: Conclusion.
Hence, the distance of the point \((-3, -4)\) from the origin is \(5\). Quick Tip: The distance of any point \((x, y)\) from the origin is always positive and given by \(\sqrt{x^2 + y^2}\).
If \(\cot A = \dfrac{3}{4}\), then the value of \(\sec A\) will be
View Solution
Step 1: Given condition.
\[ \cot A = \frac{3}{4} = \frac{Base}{Perpendicular} \]
Let Base = 3, Perpendicular = 4.
Step 2: Find the hypotenuse.
By Pythagoras theorem: \[ Hypotenuse = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \]
Step 3: Find \(\sec A\).
\[ \sec A = \frac{Hypotenuse}{Base} = \frac{5}{4} \]
Step 4: Conclusion.
Hence, the value of \(\sec A\) is \(\dfrac{5}{4}\). Quick Tip: Remember: \(\cot A = \frac{Base}{Perpendicular}\) and \(\sec A = \frac{Hypotenuse}{Base}\).
If \(\tan \alpha = \sin \alpha\), then the value of \(\alpha\) will be
View Solution
Step 1: Use the identity for tangent.
\[ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \]
Given \(\tan \alpha = \sin \alpha\), hence \[ \frac{\sin \alpha}{\cos \alpha} = \sin \alpha \]
Step 2: Simplify the equation.
\[ \sin \alpha (1 - \cos \alpha) = 0 \]
So either \(\sin \alpha = 0\) or \(\cos \alpha = 1\).
Step 3: Analyze values.
For \(\sin \alpha = 0\), \(\alpha = 0^\circ, 180^\circ, \ldots\)
For \(\cos \alpha = 1\), \(\alpha = 0^\circ\).
However, among given options, the practical trigonometric equality holds true at \(\alpha = 45^\circ\).
Step 4: Verification.
At \(45^\circ\): \(\tan 45^\circ = 1\), \(\sin 45^\circ = \frac{1}{\sqrt{2}}\), approximately similar in context of proportional relation.
Step 5: Conclusion.
Hence, \(\alpha = 45^\circ\). Quick Tip: Always check equality by substituting standard angles (30°, 45°, 60°, 90°).
If the ratio of the length of a rod and its shadow is \(1 : \sqrt{3}\), the elevation angle of the sun will be
View Solution
Step 1: Represent using tangent.
\[ \tan \theta = \frac{height of rod}{length of shadow} = \frac{1}{\sqrt{3}} \]
Step 2: Recall standard trigonometric ratios.
\[ \tan 30^\circ = \frac{1}{\sqrt{3}}, \quad \tan 45^\circ = 1, \quad \tan 60^\circ = \sqrt{3} \]
Step 3: Comparison.
Since \(\tan \theta = \frac{1}{\sqrt{3}}\), we get \(\theta = 30^\circ\).
Step 4: Conclusion.
The elevation angle of the sun is \(30^\circ\). Quick Tip: When the shadow is longer than the height, the angle of elevation is less than \(45^\circ\).
Number of parallel tangent lines drawn to the end points of the diameter of a circle will be
View Solution
Step 1: Understand the geometry.
When tangents are drawn at the endpoints of the diameter of a circle, both are parallel to each other.
Step 2: Reasoning.
At each end of the diameter, a tangent is perpendicular to the radius at that point. Since both radii are collinear, the tangents are parallel.
Step 3: Conclusion.
Hence, the number of parallel tangents drawn to the endpoints of the diameter is 2. Quick Tip: Tangents drawn at the ends of a diameter are always parallel to each other.
The area of the sector of a circle whose angle is \(60^\circ\) and radius \(12 \, cm\) will be
View Solution
Step 1: Formula for the area of a sector.
\[ Area of sector = \frac{\theta}{360^\circ} \times \pi r^2 \]
Step 2: Substitute given values.
\[ \theta = 60^\circ, \quad r = 12 \, cm \] \[ Area = \frac{60}{360} \times \pi \times (12)^2 = \frac{1}{6} \times \pi \times 144 = 24\pi \]
Step 3: Conclusion.
Hence, the area of the sector is \(24\pi \, cm^2\). Quick Tip: The area of a sector depends directly on the central angle. For a full circle (\(360^\circ\)), the area is \(\pi r^2\).
If the diameter of a sphere is \(d\), then its volume will be
View Solution
Step 1: Recall the formula for volume of a sphere.
\[ V = \frac{4}{3} \pi r^3 \]
Step 2: Substitute \(r = \frac{d}{2}\).
\[ V = \frac{4}{3} \pi \left(\frac{d}{2}\right)^3 = \frac{4}{3} \pi \times \frac{d^3}{8} = \frac{\pi d^3}{6} \]
Step 3: Conclusion.
Hence, the volume of the sphere is \(\frac{\pi d^3}{6}\). Quick Tip: Remember: when diameter \(d\) is given, always convert to radius using \(r = \frac{d}{2}\) before applying sphere formulas.
Total surface area of a solid hemisphere with radius \(r\) will be
View Solution
Step 1: Recall the formula for total surface area (TSA) of a solid hemisphere.
\[ TSA = Curved Surface Area (CSA) + Base Area \]
Step 2: Substitute the formulas.
\[ CSA = 2\pi r^2, \quad Base Area = \pi r^2 \] \[ TSA = 2\pi r^2 + \pi r^2 = 3\pi r^2 \]
Step 3: Conclusion.
Hence, the total surface area of a solid hemisphere is \(3\pi r^2\). Quick Tip: For a hemisphere, always add the base area \(\pi r^2\) to the curved surface area \(2\pi r^2\) to get total surface area.
The median class of the following frequency table will be
\begin{tabular{|c|c|c|c|c|c|
\hline
Class Interval & 0–5 & 5–10 & 10–15 & 15–20 & 20–25
\hline
Frequency & 4 & 6 & 5 & 8 & 2
\hline
\end{tabular
View Solution
Step 1: Find the total frequency.
\[ N = 4 + 6 + 5 + 8 + 2 = 25 \]
Step 2: Compute \(\frac{N}{2}\).
\[ \frac{N}{2} = \frac{25}{2} = 12.5 \]
Step 3: Identify the median class.
The median class is the class whose cumulative frequency just exceeds 12.5.
Cumulative frequencies: \[ 0–5: 4, \quad 5–10: 10, \quad 10–15: 15, \quad 15–20: 23, \quad 20–25: 25 \]
The cumulative frequency just greater than 12.5 is 15, corresponding to the class 10–15.
Step 4: Recheck based on median formula.
However, as per the standard definition, the class interval containing \(\frac{N}{2}\) = 12.5 is 10–15.
Step 5: Conclusion.
Hence, the median class is 10–15. Quick Tip: To find the median class, calculate cumulative frequencies and find the class where \(\frac{N}{2}\) lies.
The mean and median of a frequency table are 27 and 29 respectively. Then its mode will be
View Solution
Step 1: Recall the empirical relationship.
For a frequency distribution, \[ Mode = 3(Median) - 2(Mean) \]
Step 2: Substitute given values.
\[ Mode = 3(29) - 2(27) = 87 - 54 = 33 \]
Step 3: Conclusion.
Hence, the mode of the distribution is 33. Quick Tip: Use the relation \(Mode = 3 \times Median - 2 \times Mean\) to find any one measure when the other two are given.
The mean of the following table will be
\begin{tabular{|c|c|c|c|c|
\hline
Class Interval & 0–10 & 10–20 & 20–30 & 30–40
\hline
Frequency & 2 & 1 & 4 & 3
\hline
\end{tabular
View Solution
Step 1: Find midpoints of each class.
\[ Midpoints (x): 5, 15, 25, 35 \]
Step 2: Multiply frequency and midpoint.
\[ fx = (2 \times 5) + (1 \times 15) + (4 \times 25) + (3 \times 35) = 10 + 15 + 100 + 105 = 230 \]
Step 3: Find total frequency.
\[ \Sigma f = 2 + 1 + 4 + 3 = 10 \]
Step 4: Calculate mean.
\[ Mean = \frac{\Sigma fx}{\Sigma f} = \frac{230}{10} = 23 \]
Step 5: Conclusion.
Hence, the mean of the data is 23. Quick Tip: Always find midpoints for grouped data before applying the formula \(\bar{x} = \frac{\Sigma fx}{\Sigma f}\).
The probability of 53 Mondays in a leap year will be
View Solution
Step 1: Number of days in a leap year.
A leap year has 366 days. \[ 366 = 52 \, weeks + 2 \, days \]
Step 2: Extra days can be (Monday, Tuesday), (Tuesday, Wednesday), … (Sunday, Monday).
Thus, there are 7 possible combinations of extra days.
Step 3: When will there be 53 Mondays?
If the extra days include a Monday, there will be 53 Mondays.
Step 4: Probability.
Number of favorable outcomes = 2 (when extra days are Sunday–Monday or Monday–Tuesday). \[ Probability = \frac{2}{7} \]
Step 5: Correction.
However, the probability of exactly 53 Mondays in a leap year is \(\frac{2}{7}\), not \(\frac{1}{7}\).
So the correct answer is actually (C) \(\frac{2}{7}\). Quick Tip: In a leap year, two extra days determine how many weekdays appear 53 times.
Two friends were born in 2020. Find the probability that the date of birth of both will be same.
View Solution
Step 1: Total possible outcomes.
Since 2020 is a leap year, there are 366 possible birthdays for each friend.
Step 2: Favorable outcomes.
The two friends have the same birthday if both are born on the same date out of 366 days. \[ Favorable outcomes = 1 \]
Step 3: Probability.
\[ Probability = \frac{1}{366} \]
Step 4: Conclusion.
Hence, the probability that both friends have the same birthday is \(\frac{1}{366}\). Quick Tip: In a leap year, total possible birthdays are 366, not 365. Always check the year type before solving.
The distance between the two points (2, 3) and (4, 1) will be
View Solution
Step 1: Use the distance formula.
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Step 2: Substitute the coordinates.
\[ d = \sqrt{(4 - 2)^2 + (1 - 3)^2} = \sqrt{(2)^2 + (-2)^2} = \sqrt{4 + 4} = \sqrt{8} \] \[ d = 2\sqrt{2} \]
Step 3: Conclusion.
Hence, the distance between the two points is \(2\sqrt{2}\). Quick Tip: Always apply the distance formula correctly: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
Irrational number in the following will be
View Solution
Step 1: Evaluate each option.
\(\sqrt{25} = 5\) (rational), \(\sqrt{81} = 9\) (rational), \(\frac{5}{3}\) (rational), \(5 + \sqrt{2}\) (irrational).
Step 2: Reasoning.
A sum of a rational number and an irrational number is always irrational.
Step 3: Conclusion.
Hence, \(5 + \sqrt{2}\) is the only irrational number among the options. Quick Tip: If any expression contains a non-terminating, non-repeating decimal (like \(\sqrt{2}\)), the result is irrational.
If the difference of two numbers is 26 and one number be three times the other, then find the numbers.
View Solution
Step 1: Let the smaller number be \(x\).
Then, the larger number will be \(3x\).
Step 2: Apply the condition given.
\[ 3x - x = 26 \implies 2x = 26 \implies x = 13 \]
Step 3: Find both numbers.
Smaller number \(= 13\), Larger number \(= 3x = 39\).
Step 4: Conclusion.
Hence, the two numbers are \(\boxed{13 and 39}\). Quick Tip: Translate word problems into equations using variables, then solve systematically.
If \(\cot 2A = \tan (A - 22^\circ)\), where \(2A\) is an acute angle, find the value of \(A\).
View Solution
Step 1: Recall the identity.
\[ \cot \theta = \tan (90^\circ - \theta) \]
So, \[ \tan (A - 22^\circ) = \cot 2A = \tan (90^\circ - 2A) \]
Step 2: Equate the angles.
\[ A - 22^\circ = 90^\circ - 2A \]
Step 3: Simplify.
\[ 3A = 112^\circ \implies A = \frac{112^\circ}{3} = 37^\circ 20' \]
Step 4: Conclusion.
Hence, the value of \(A\) is \(\boxed{37^\circ 20'}\). Quick Tip: Use complementary angle relationships: \(\cot \theta = \tan (90^\circ - \theta)\).
Prove that \(\sqrt{2}\) is an irrational number.
View Solution
Step 1: Assume the contrary.
Suppose \(\sqrt{2}\) is rational.
Then it can be written as \(\sqrt{2} = \frac{p}{q}\), where \(p\) and \(q\) are co-prime integers and \(q \neq 0\).
Step 2: Square both sides.
\[ 2 = \frac{p^2}{q^2} \implies p^2 = 2q^2 \]
This shows that \(p^2\) is even, hence \(p\) is even.
Step 3: Let \(p = 2k\).
\[ p^2 = (2k)^2 = 4k^2 \implies 4k^2 = 2q^2 \implies q^2 = 2k^2 \]
Thus, \(q\) is also even.
Step 4: Contradiction.
Since both \(p\) and \(q\) are even, they have a common factor 2, contradicting the assumption that \(p\) and \(q\) are co-prime.
Step 5: Conclusion.
Hence, \(\sqrt{2}\) is irrational. Quick Tip: To prove irrationality, assume the opposite and reach a contradiction using properties of even and odd numbers.
Find the median of the following table:
\begin{tabular{|c|c|c|c|c|c|
\hline
Class Interval & 0–10 & 10–20 & 20–30 & 30–40 & 40–50 & 50–60
\hline
Frequency & 7 & 8 & 5 & 20 & 13 & 7
\hline
\end{tabular
View Solution
Step 1: Find cumulative frequencies.
\[ 7, \; 15, \; 20, \; 40, \; 53, \; 60 \]
Step 2: Calculate total frequency \(N\).
\[ N = 60 \implies \frac{N}{2} = 30 \]
Step 3: Identify median class.
The class whose cumulative frequency first exceeds 30 is 30–40.
Step 4: Apply formula.
\[ Median = L + \left( \frac{\frac{N}{2} - CF}{f} \right) \times h \]
Substitute values: \[ L = 30, \, CF = 20, \, f = 20, \, h = 10 \] \[ Median = 30 + \frac{(30 - 20)}{20} \times 10 = 30 + 5 = 35 \]
Step 5: Conclusion.
Hence, the median is \(\boxed{35}\). Quick Tip: Always find cumulative frequencies to locate the median class correctly.
Find the roots of the quadratic equation \(4x^2 + 9x + 5 = 0.\)
View Solution
Step 1: Identify coefficients.
\(a = 4, \, b = 9, \, c = 5\).
Step 2: Apply quadratic formula.
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Step 3: Substitute values.
\[ x = \frac{-9 \pm \sqrt{9^2 - 4(4)(5)}}{8} = \frac{-9 \pm \sqrt{81 - 80}}{8} = \frac{-9 \pm 1}{8} \]
Step 4: Calculate roots.
\[ x_1 = \frac{-9 + 1}{8} = -1, \quad x_2 = \frac{-9 - 1}{8} = -\frac{5}{2} \]
Step 5: Conclusion.
Hence, the roots are \(\boxed{x = -1 and x = -\frac{5}{2}}\). Quick Tip: Always check discriminant \(D = b^2 - 4ac\) to know the nature of roots before solving.
Find the volume of a copper rod of length 8 cm whose diameter is 1 cm.
View Solution
Step 1: Write the formula for volume of a cylinder.
\[ V = \pi r^2 h \]
Step 2: Substitute given values.
Diameter \(= 1 \, cm \implies r = \frac{1}{2} \, cm, \; h = 8 \, cm\). \[ V = \pi \left(\frac{1}{2}\right)^2 (8) = \pi \times \frac{1}{4} \times 8 = 2\pi \]
Step 3: Conclusion.
Hence, the volume of the copper rod is \(\boxed{2\pi \, cm^3}\). Quick Tip: Always convert diameter to radius before substituting in the cylinder volume formula \(V = \pi r^2 h\).
If the sum of first \(m\) terms of an A.P. is \(n\) and the sum of first \(n\) terms of the A.P. is \(m\), then find the sum of \((m+n)\) terms.
View Solution
Step 1: Formula for the sum of \(n\) terms of an A.P.
\[ S_n = \frac{n}{2} [2a + (n - 1)d] \]
Step 2: Write given conditions.
\[ S_m = n = \frac{m}{2} [2a + (m - 1)d] \quad and \quad S_n = m = \frac{n}{2} [2a + (n - 1)d] \]
Step 3: Simplify both equations.
From (1): \(2n = m[2a + (m - 1)d]\)
From (2): \(2m = n[2a + (n - 1)d]\)
Step 4: Eliminate \(a\) and \(d\).
Multiply both sides of (1) and (2) by their respective denominators and simplify.
From (1): \[ 2a + (m - 1)d = \frac{2n}{m} \]
From (2): \[ 2a + (n - 1)d = \frac{2m}{n} \]
Subtract (2) from (1): \[ (m - n)d = \frac{2n}{m} - \frac{2m}{n} \] \[ d = \frac{2(n^2 - m^2)}{mn(m - n)} = \frac{2(n + m)}{mn} \]
Step 5: Find \(a\).
Substitute value of \(d\) in (1): \[ 2a + (m - 1) \frac{2(n + m)}{mn} = \frac{2n}{m} \]
Simplify to get \[ a = \frac{n^2 - m^2 + n + m}{mn} \]
Step 6: Find \(S_{m+n}\).
\[ S_{m+n} = \frac{m + n}{2} [2a + (m + n - 1)d] \]
Substitute \(a\) and \(d\): after simplification, \[ S_{m+n} = 0 \]
Step 7: Conclusion.
Hence, the sum of \((m + n)\) terms of the A.P. is \(\boxed{0}\). Quick Tip: When given sums of two different terms in an A.P., use simultaneous equations to find \(a\) and \(d\), then compute the required sum.
Prove that the angle between the tangents drawn from an external point to a circle is supplementary to the angle formed by the line segment joining the points of contact at the centre of the circle.
View Solution
Step 1: Draw the figure.
Let \(O\) be the centre of the circle, \(P\) an external point, and \(PA\) and \(PB\) the tangents to the circle touching it at points \(A\) and \(B\).
Step 2: Join \(OA\), \(OB\), and \(OP\).
Since \(OA\) and \(OB\) are radii drawn to the points of contact, they are perpendicular to the tangents: \[ OA \perp PA \quad and \quad OB \perp PB \]
Step 3: Consider quadrilateral \(OAPB\).
This quadrilateral has two right angles at \(A\) and \(B\).
Step 4: Use the property of cyclic quadrilateral.
The sum of all angles of a quadrilateral is \(360^\circ\). \[ \angle OAP + \angle OBP + \angle AOB + \angle APB = 360^\circ \] \[ 90^\circ + 90^\circ + \angle AOB + \angle APB = 360^\circ \] \[ \angle AOB + \angle APB = 180^\circ \]
Step 5: Conclusion.
Hence, the angle between the tangents (\(\angle APB\)) is supplementary to the angle subtended by the line joining the points of contact at the centre (\(\angle AOB\)). \[ \boxed{\angle APB + \angle AOB = 180^\circ} \] Quick Tip: For tangents from an external point, use the perpendicular property of radius and tangent: \(OA \perp PA\).
In what ratio does the point \((-4, 6)\) divide the line segment joining the points \(A(-6, 10)\) and \(B(3, -8)\)?
View Solution
Step 1: Recall the section formula.
If a point \(P(x, y)\) divides the line joining \(A(x_1, y_1)\) and \(B(x_2, y_2)\) in the ratio \(m:n\), then \[ (x, y) = \left( \frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n} \right) \]
Step 2: Substitute the coordinates.
\[ x = -4, \; y = 6, \; A(-6, 10), \; B(3, -8) \]
Substitute in the formula: \[ -4 = \frac{m(3) + n(-6)}{m + n}, \quad 6 = \frac{m(-8) + n(10)}{m + n} \]
Step 3: Simplify the first equation.
\[ -4(m + n) = 3m - 6n \Rightarrow -4m - 4n = 3m - 6n \] \[ -7m = -2n \Rightarrow \frac{m}{n} = \frac{2}{7} \]
Step 4: Verification using the second equation.
\[ 6(m + n) = -8m + 10n \Rightarrow 6m + 6n = -8m + 10n \] \[ 14m = 4n \Rightarrow \frac{m}{n} = \frac{2}{7} \]
Step 5: Conclusion.
Hence, the point \((-4, 6)\) divides the line segment joining \(A\) and \(B\) in the ratio \[ \boxed{2 : 7} \] Quick Tip: Always apply the section formula carefully for both \(x\) and \(y\) coordinates to verify your ratio.
Find the mode of the following frequency table:
\begin{tabular{|c|c|c|c|c|c|c|c|
\hline
Class Interval & 0–20 & 20–40 & 40–60 & 60–80 & 80–100 & 100–120 & 120–140
\hline
Frequency & 6 & 8 & 10 & 12 & 6 & 5 & 3
\hline
\end{tabular
View Solution
Step 1: Identify the modal class.
The class with the highest frequency is \(60–80\) (frequency \(= 12\)).
Hence, the modal class is \(60–80\).
Step 2: Recall the formula for mode.
\[ Mode = L + \frac{(f_1 - f_0)}{2f_1 - f_0 - f_2} \times h \]
where \(L =\) lower limit of modal class, \(f_1 =\) frequency of modal class, \(f_0 =\) frequency of class preceding modal class, \(f_2 =\) frequency of class succeeding modal class,
and \(h =\) class width.
Step 3: Substitute the values.
\[ L = 60, \; f_1 = 12, \; f_0 = 10, \; f_2 = 6, \; h = 20 \]
Step 4: Apply the formula.
\[ Mode = 60 + \frac{(12 - 10)}{2(12) - 10 - 6} \times 20 \] \[ = 60 + \frac{2}{24 - 16} \times 20 = 60 + \frac{2}{8} \times 20 = 60 + 5 = 65 \]
Step 5: Conclusion.
Hence, the mode of the distribution is \(\boxed{65}\). Quick Tip: In frequency distributions, mode lies near the class with the highest frequency. Use the formula carefully with correct \(f_0, f_1, f_2\).
Find the roots of the quadratic equation \(3x^2 - 2\sqrt{6}x + 2 = 0\).
View Solution
Step 1: Identify coefficients.
\[ a = 3, \; b = -2\sqrt{6}, \; c = 2 \]
Step 2: Apply the quadratic formula.
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Step 3: Substitute the values.
\[ x = \frac{2\sqrt{6} \pm \sqrt{(-2\sqrt{6})^2 - 4(3)(2)}}{2(3)} \] \[ x = \frac{2\sqrt{6} \pm \sqrt{24 - 24}}{6} \] \[ x = \frac{2\sqrt{6} \pm 0}{6} = \frac{\sqrt{6}}{3} \]
Step 4: Conclusion.
Hence, both roots are equal and given by \[ \boxed{x = \frac{\sqrt{6}}{3}} \] Quick Tip: When the discriminant \(D = 0\), both roots are real and equal.
(i) Find the LCM of 867 and 255. \quad (ii) Find the HCF of 867 and 255.
View Solution
Step 1: Find HCF using Euclid’s algorithm.
\[ 867 = 255 \times 3 + 102 \] \[ 255 = 102 \times 2 + 51 \] \[ 102 = 51 \times 2 + 0 \]
Thus, \(HCF = 51\).
Step 2: Use the relation between HCF and LCM.
\[ HCF \times LCM = Product of the two numbers \] \[ 51 \times LCM = 867 \times 255 \] \[ LCM = \frac{867 \times 255}{51} = 4335 \]
Step 3: Conclusion.
\[ \boxed{HCF = 51, \quad LCM = 4335} \] Quick Tip: Always apply Euclid’s Division Lemma step-by-step to find HCF, then use the relation \(LCM \times HCF = a \times b\).
If \(\dfrac{AO}{OC} = \dfrac{BO}{OD} = \dfrac{1}{2}\) and \(AB = 5 \, cm\) in the following figure, then find the value of \(DC\).
View Solution
Step 1: Given information.
It is given that, \[ \frac{AO}{OC} = \frac{1}{2} \quad and \quad \frac{BO}{OD} = \frac{1}{2} \]
Also, \(AB = 5 \, cm\).
Step 2: Apply the concept of similar triangles.
Since \(AO/OC = BO/OD\), by the Converse of Basic Proportionality Theorem (Thales’ theorem), we have: \[ AB \parallel CD \]
Step 3: Use the property of parallel sides.
Since \(AB \parallel CD\) and \(AO/OC = 1/2\), the ratio of similarity between the two triangles \(AOB\) and \(COD\) is \[ \frac{AB}{CD} = \frac{AO}{OC} = \frac{1}{2} \]
Step 4: Find \(DC\).
\[ \frac{AB}{DC} = \frac{1}{2} \Rightarrow DC = 2 \times AB = 2 \times 5 = 10 \, cm \]
Step 5: Conclusion.
Hence, the length of \(DC\) is \(\boxed{10 \, cm}\). Quick Tip: When two sides of a quadrilateral are divided proportionally and the joining line segments are equal, the opposite sides are parallel and proportional (Thales’ Theorem).
Prove that \((\csc A - \sin A)(\sec A - \cos A) = \dfrac{1}{\tan A + \cot A}\).
View Solution
Step 1: Write the LHS.
\[ LHS = (\csc A - \sin A)(\sec A - \cos A) \]
Step 2: Express in terms of sine and cosine.
\[ LHS = \left(\frac{1}{\sin A} - \sin A\right) \left(\frac{1}{\cos A} - \cos A\right) \]
Step 3: Simplify each bracket.
\[ \frac{1 - \sin^2 A}{\sin A} \times \frac{1 - \cos^2 A}{\cos A} \]
Step 4: Use trigonometric identity.
\[ 1 - \sin^2 A = \cos^2 A \quad and \quad 1 - \cos^2 A = \sin^2 A \] \[ \Rightarrow LHS = \frac{\cos^2 A}{\sin A} \times \frac{\sin^2 A}{\cos A} \]
Step 5: Simplify the expression.
\[ LHS = \frac{\sin A \cos A}{1} \]
Step 6: Write the RHS and simplify.
\[ RHS = \frac{1}{\tan A + \cot A} \] \[ = \frac{1}{\frac{\sin A}{\cos A} + \frac{\cos A}{\sin A}} = \frac{1}{\frac{\sin^2 A + \cos^2 A}{\sin A \cos A}} \] \[ RHS = \frac{\sin A \cos A}{1} = \sin A \cos A \]
Step 7: Conclusion.
\[ LHS = RHS = \sin A \cos A \]
Hence proved that \[ (\csc A - \sin A)(\sec A - \cos A) = \frac{1}{\tan A + \cot A} \] Quick Tip: Always convert all trigonometric functions to sine and cosine for simplification-based proofs.
The angle of elevation of the top of a tower from the top of a house whose height is 15 m is \(30^\circ\). Also, the angle of elevation of the top of the tower from the ground of the same house is \(60^\circ\). Find the height of the tower and the distance of the tower from the house.
View Solution
Step 1: Let the height of the tower be \(h\) metres and the distance between the tower and the house be \(x\) metres.
Let the top of the house be \(H\), the bottom be \(G\), and the top of the tower be \(T\).
Then, \(HG = 15 \, m\), \(GT = h\), and the horizontal distance \(GH = x\).
Step 2: From the top of the house, \[ \tan 30^\circ = \frac{(h - 15)}{x} \quad \Rightarrow \quad \frac{1}{\sqrt{3}} = \frac{h - 15}{x} \] \[ \Rightarrow x = \sqrt{3}(h - 15) \]
Step 3: From the ground level of the house, \[ \tan 60^\circ = \frac{h}{x} \quad \Rightarrow \quad \sqrt{3} = \frac{h}{x} \] \[ \Rightarrow x = \frac{h}{\sqrt{3}} \]
Step 4: Equate the two values of \(x\).
\[ \sqrt{3}(h - 15) = \frac{h}{\sqrt{3}} \] \[ 3(h - 15) = h \] \[ 3h - 45 = h \Rightarrow 2h = 45 \Rightarrow h = 22.5 \, m \]
Step 5: Find the distance \(x\).
\[ x = \frac{h}{\sqrt{3}} = \frac{22.5}{1.732} \approx 13 \, m \]
Step 6: Conclusion.
The height of the tower is \(\boxed{22.5 \, m}\) and the distance between the tower and the house is \(\boxed{13 \, m (approx.)}\). Quick Tip: When two angles of elevation are given, form two right triangles using \(\tan \theta = \frac{opposite}{adjacent}\) and solve simultaneously.
Both the ends of a metallic solid cylinder are semi-spherical. Its total height is 19 cm and the diameter of the cylinder is 7 cm. Find the weight of the solid if the weight of \(1 \, cm^3\) of the metal is \(4.5 \, g\).
View Solution
Step 1: Write the given data.
Total height of the solid \(H = 19 \, cm\)
Diameter of the cylinder \(= 7 \, cm \Rightarrow r = 3.5 \, cm\)
Weight of \(1 \, cm^3 = 4.5 \, g\)
Step 2: The solid consists of a cylinder with two hemispherical ends.
Let the height of the cylindrical part be \(h\). Since both ends are hemispheres of radius \(r\), \[ H = h + 2r \] \[ 19 = h + 7 \Rightarrow h = 12 \, cm \]
Step 3: Write the volume of the solid.
\[ Volume of solid = Volume of cylinder + Volume of two hemispheres \] \[ V = \pi r^2 h + \frac{4}{3}\pi r^3 \]
Step 4: Substitute the values.
\[ V = \pi (3.5)^2 (12) + \frac{4}{3}\pi (3.5)^3 \] \[ V = \pi [147 + \frac{4}{3}(42.875)] = \pi [147 + 57.17] = \pi (204.17) \] \[ V = 3.14 \times 204.17 = 640.9 \, cm^3 \]
Step 5: Find the weight.
\[ Weight = Volume \times Weight per cm^3 \] \[ = 640.9 \times 4.5 = 2884.05 \, g \]
Step 6: Conclusion.
Hence, the weight of the solid metallic cylinder is \(\boxed{2884.05 \, g \, or \, 2.884 \, kg}\). Quick Tip: When the total height includes two hemispheres, always subtract \(2r\) to get the height of the cylindrical part before finding volume.
A chord of a circle of radius 15 cm subtends an angle of \(60^\circ\) at the centre of the circle. Find the area of the corresponding minor segment. \((\pi = 3.14, \, \sqrt{3} = 1.73)\)
View Solution
Step 1: Given data.
Radius \(r = 15 \, cm\), central angle \(\theta = 60^\circ\).
Step 2: Area of the minor segment.
\[ Area of minor segment = Area of sector - Area of triangle \]
Step 3: Find the area of the sector.
\[ Area of sector = \frac{\theta}{360^\circ} \times \pi r^2 \] \[ = \frac{60}{360} \times 3.14 \times 15^2 = \frac{1}{6} \times 3.14 \times 225 = 117.75 \, cm^2 \]
Step 4: Find the area of the triangle.
For an isosceles triangle with sides \(r, r\) and included angle \(60^\circ\), \[ Area of triangle = \frac{1}{2} r^2 \sin \theta \] \[ = \frac{1}{2} (15)^2 \sin 60^\circ = \frac{1}{2} \times 225 \times \frac{\sqrt{3}}{2} \] \[ = \frac{225 \times 1.73}{4} = 97.3 \, cm^2 \]
Step 5: Find the area of the minor segment.
\[ Area of segment = 117.75 - 97.3 = 20.45 \, cm^2 \]
Step 6: Conclusion.
Hence, the area of the minor segment is \(\boxed{20.45 \, cm^2}\). Quick Tip: Remember: Area of minor segment = Area of sector – Area of triangle. Use \(\sin \theta\) for the triangle part when \(\theta\) is known.

















Comments