The Bihar Board 2024 Class 10th Maths exam is being conducted (February 16, 2024). The question paper along with the solution PDF will be available here to download once the exam is conducted successfully.
The Bihar Board 10th Boards Maths exam is expected to be easy to moderate based on previous year trends. The Maths exam Real Numbers, Polynomials, Linear Equations, Quadratic Equations, Arithmetic Progression, Coordinate Geometry, Trigonometry, Circles, Constructions, Areas Related to Circles, Surface Areas and Volumes, Statistics, and Probability.
Bihar Board Class 10 (Set J) Maths Question Paper 2024 with Solutions
| Bihar Board Class 10 Maths Question Paper with Answer Key | Check Solution |
Bihar Board Class 10 Maths Question Paper 2024 with Solutions
Section-A
If \( P \left( \frac{a}{2}, 4 \right) \) is the midpoint of the line segment joining the points \( A(-6,5) \) and \( B(-2,3) \), then the value of \( a \) is:
View Solution
The midpoint formula states:
\[ \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]
Given points: \( A(-6,5) \) and \( B(-2,3) \),
\[ \left( \frac{-6 + (-2)}{2}, \frac{5 + 3}{2} \right) = \left( \frac{-8}{2}, \frac{8}{2} \right) = (-4,4) \]
Comparing with \( P \left( \frac{a}{2}, 4 \right) \), we get:
\[ \frac{a}{2} = -4 \quad \Rightarrow \quad a = -4 \]
\begin{quicktipbox
The midpoint formula is useful to find the average of two coordinates: \[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]
\end{quicktipbox Quick Tip: The midpoint formula is useful to find the average of two coordinates: \[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]
If three points are collinear then what is the area of the triangle formed by them?
View Solution
If three points are collinear, they lie on the same straight line. The area of a triangle is given by:
\[ Area = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
Since all three points are collinear, substituting their coordinates in the above formula results in zero.
\begin{quicktipbox
Collinear points mean they lie on the same straight line. The area of any triangle formed by collinear points is always zero.
\end{quicktipbox Quick Tip: Collinear points mean they lie on the same straight line. The area of any triangle formed by collinear points is always zero.
If \( A(-1,0) \), \( B(5,-2) \), and \( C(8,2) \) are the vertices of a triangle \( \triangle ABC \), then the coordinates of its centroid are:
View Solution
The centroid formula states:
\[ G \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \]
Substituting the given coordinates:
\[ G \left( \frac{-1 + 5 + 8}{3}, \frac{0 + (-2) + 2}{3} \right) = G \left( \frac{12}{3}, \frac{0}{3} \right) = (4,0) \]
\begin{quicktipbox
The centroid of a triangle is the average of the coordinates of its vertices: \[ G = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \]
\end{quicktipbox Quick Tip: The centroid of a triangle is the average of the coordinates of its vertices: \[ G = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \]
If in \( \triangle ABC \), \( AD \) is the bisector of \( \angle BAC \) and \( AB = 10 \) cm, \( AC = 14 \) cm, \( BC = 6 \) cm, then the value of \( DC \) is:
View Solution
Using the angle bisector theorem:
\[ \frac{BD}{DC} = \frac{AB}{AC} = \frac{10}{14} = \frac{5}{7} \]
Since \( BC = 6 \) cm, let \( BD = x \) and \( DC = 6 - x \).
\[ \frac{x}{6-x} = \frac{5}{7} \]
Solving for \( x \):
\[ 7x = 5(6 - x) \]
\[ 7x = 30 - 5x \]
\[ 12x = 30 \]
\[ x = 2.5, \quad DC = 6 - 2.5 = 3.5 \]
\begin{quicktipbox
The angle bisector theorem states: \[ \frac{BD}{DC} = \frac{AB}{AC} \]
Use this ratio to solve for missing segment lengths.
\end{quicktipbox Quick Tip: The angle bisector theorem states: \[ \frac{BD}{DC} = \frac{AB}{AC} \] Use this ratio to solve for missing segment lengths.
In \( \triangle ABC \), \( DE \parallel BC \) such that \( \frac{AD}{DB} = \frac{3}{5} \). If \( AC = 5.6 \) cm, then \( AE \) is:
View Solution
Since \( DE \parallel BC \), by the Basic Proportionality Theorem (Thales' Theorem), we get:
\[ \frac{AD}{DB} = \frac{AE}{EC} \]
Given \( \frac{AD}{DB} = \frac{3}{5} \), this means:
\[ \frac{AE}{EC} = \frac{3}{5} \]
Since \( AC = AE + EC = 5.6 \), let \( AE = x \), then \( EC = 5.6 - x \).
\[ \frac{x}{5.6 - x} = \frac{3}{5} \]
Cross multiplying:
\[ 5x = 3(5.6 - x) \]
\[ 5x = 16.8 - 3x \]
\[ 8x = 16.8 \]
\[ x = 2.8 \]
\begin{quicktipbox
The Basic Proportionality Theorem states that if a line is parallel to one side of a triangle, it divides the other two sides in the same ratio.
\end{quicktipbox Quick Tip: The Basic Proportionality Theorem states that if a line is parallel to one side of a triangle, it divides the other two sides in the same ratio.
If the ratio of corresponding sides of two similar triangles is \( 5:6 \), then the ratio of their perimeters is:
View Solution
For similar triangles, the ratio of corresponding sides, perimeters, and altitudes are the same.
Since the given ratio of sides is:
\[ 5:6 \]
The ratio of perimeters is also:
\[ 5:6 \]
\begin{quicktipbox
In similar triangles, the ratio of corresponding sides, perimeters, and altitudes remains the same, but the ratio of areas is the square of the side ratio.
\end{quicktipbox Quick Tip: In similar triangles, the ratio of corresponding sides, perimeters, and altitudes remains the same, but the ratio of areas is the square of the side ratio.
In \( \triangle ABC \), \( AB = 6\sqrt{3} \) cm, \( AC = 12 \) cm, and \( BC = 6 \) cm, then \( \angle B \) is:
View Solution
To determine the angle \( B \), we use the Cosine Rule:
\[ \cos B = \frac{AB^2 + BC^2 - AC^2}{2 \times AB \times BC} \]
Substituting the given values:
\[ \cos B = \frac{(6\sqrt{3})^2 + 6^2 - 12^2}{2 \times (6\sqrt{3}) \times 6} \]
\[ = \frac{108 + 36 - 144}{2 \times 6\sqrt{3} \times 6} \]
\[ = \frac{0}{72\sqrt{3}} \]
\[ = 0 \]
Since \( \cos B = 0 \), we get:
\[ B = 90^\circ \]
\begin{quicktipbox
If \( \cos \theta = 0 \), then \( \theta = 90^\circ \). This means the given triangle is a right-angled triangle.
\end{quicktipbox Quick Tip: If \( \cos \theta = 0 \), then \( \theta = 90^\circ \). This means the given triangle is a right-angled triangle.
If an equilateral triangle \( \triangle ABC \) has one side of 12 cm, and another equilateral triangle \( \triangle DEF \) has one side of 6 cm, then what is the ratio of their areas?
View Solution
For similar triangles, the ratio of their areas is the square of the ratio of their corresponding sides.
Given the side ratio:
\[ \frac{AB}{DE} = \frac{12}{6} = 2:1 \]
The ratio of areas is:
\[ \left(\frac{12}{6}\right)^2 = 4:1 \]
\begin{quicktipbox
For similar triangles, the ratio of their areas is given by: \[ Area Ratio = \left(\frac{Side_1}{Side_2}\right)^2 \]
\end{quicktipbox Quick Tip: For similar triangles, the ratio of their areas is given by: \[ Area Ratio = \left(\frac{Side_1}{Side_2}\right)^2 \]
In \( \triangle ABC \) and \( \triangle PQR \), which are similar triangles, \( AD \) is perpendicular to \( BC \) and \( PT \) is perpendicular to \( QR \). If \( AD = 9 \) cm and \( PT = 7 \) cm, then the ratio of the areas of triangles \( ABC \) and \( PQR \) is:
View Solution
The ratio of the areas of similar triangles is the square of the ratio of their corresponding heights.
\[ Area Ratio = \left(\frac{Height_1}{Height_2}\right)^2 \]
Substituting the values:
\[ \left(\frac{9}{7}\right)^2 = \frac{81}{49} \]
\begin{quicktipbox
For similar triangles, the ratio of their areas is: \[ \left(\frac{Height_1}{Height_2}\right)^2 \]
\end{quicktipbox Quick Tip: For similar triangles, the ratio of their areas is: \[ \left(\frac{Height_1}{Height_2}\right)^2 \]
If one side of an equilateral triangle is 12 cm, then its height is:
View Solution
The height formula of an equilateral triangle is:
\[ h = \frac{\sqrt{3}}{2} s \]
Substituting \( s = 12 \):
\[ h = \frac{\sqrt{3}}{2} \times 12 \]
\[ h = 6\sqrt{3} \]
\begin{quicktipbox
For an equilateral triangle, the height formula is: \[ h = \frac{\sqrt{3}}{2} s \]
where \( s \) is the side length.
\end{quicktipbox Quick Tip: For an equilateral triangle, the height formula is: \[ h = \frac{\sqrt{3}}{2} s \] where \( s \) is the side length.
The distance between two parallel tangents of a circle is 10 cm. Then the radius of the circle is:
View Solution
The distance between two parallel tangents is equal to twice the radius.
\[ 2r = 10 \]
\[ r = 5 \]
\begin{quicktipbox
For a circle, the distance between two parallel tangents is always twice the radius.
\end{quicktipbox Quick Tip: For a circle, the distance between two parallel tangents is always twice the radius.
If two circles touch each other externally, then what is the number of common tangents?
View Solution
When two circles touch externally, they have
- Two external common tangents
- Two internal common tangents
Thus, the total number of common tangents is 4.
\begin{quicktipbox
Two externally touching circles always have 4 common tangents (2 external and 2 internal).
\end{quicktipbox Quick Tip: Two externally touching circles always have 4 common tangents (2 external and 2 internal).
From an external point \( P \), two tangents \( PA \) and \( PB \) are drawn to a circle. If \( PA = 6 \) cm, then \( PB \) is:
View Solution
The two tangents drawn from an external point to a circle are always equal in length.
Since \( PA = 6 \) cm, we directly get:
\[ PB = PA = 6 cm \]
\begin{quicktipbox
The two tangents drawn from an external point to a circle are always equal: \[ PA = PB \]
\end{quicktipbox Quick Tip: The two tangents drawn from an external point to a circle are always equal: \[ PA = PB \]
If two tangents drawn on a circle of radius 3 cm are inclined to each other at an angle of \(60^\circ\), then the length of each tangent is:
View Solution
Step 1: Understanding the given problem
A circle of radius \( r = 3 \) cm has two tangents inclined at an angle of \( 60^\circ \).
Each tangent's length can be found using the formula: \[ l = r \tan \frac{\theta}{2} \]
where \( \theta = 60^\circ \) (angle between tangents).
Step 2: Applying the formula \[ l = 3 \times \tan \frac{60^\circ}{2} = 3 \times \tan 30^\circ \] \[ \tan 30^\circ = \frac{1}{\sqrt{3}} \] \[ l = 3 \times \frac{1}{\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3} \times \frac{3}{3} = 2\sqrt{3} cm \]
Thus, the correct answer is option (1) \( 2\sqrt{3} \) cm. Quick Tip: For problems involving tangents to a circle, use the formula \( l = r \tan \frac{\theta}{2} \) to find the length of the tangents when given the angle between them.
If \( \sin(20^\circ + \theta) = \cos 30^\circ \), then the value of \( \theta \) is:
View Solution
Using the trigonometric identity:
\[ \sin x = \cos(90^\circ - x) \]
We rewrite the given equation:
\[ \sin(20^\circ + \theta) = \cos 30^\circ \]
\[ \sin(20^\circ + \theta) = \sin(90^\circ - 30^\circ) \]
\[ \sin(20^\circ + \theta) = \sin 60^\circ \]
Since the sine values are equal, we equate the angles:
\[ 20^\circ + \theta = 60^\circ \]
\[ \theta = 60^\circ - 20^\circ \]
\[ \theta = 50^\circ \]
\begin{quicktipbox
Using the identity: \[ \sin x = \cos (90^\circ - x) \]
convert the equation into sine terms and solve for \( \theta \).
\end{quicktipbox Quick Tip: Using the identity: \[ \sin x = \cos (90^\circ - x) \] convert the equation into sine terms and solve for \( \theta \).
If in \( \triangle ABC \), \( \angle C = 90^\circ \), then \( \sin(A + B) \) is:
View Solution
In any triangle:
\[ A + B + C = 180^\circ \]
Since \( C = 90^\circ \):
\[ A + B = 90^\circ \]
Thus:
\[ \sin (A + B) = \sin 90^\circ = 1 \]
\begin{quicktipbox
In a right-angled triangle, the sum of the other two angles is always \( 90^\circ \).
\end{quicktipbox Quick Tip: In a right-angled triangle, the sum of the other two angles is always \( 90^\circ \).
\( \sec^2 23^\circ - \tan^2 23^\circ + 2 \) is:
View Solution
Using the trigonometric identity:
\[ \sec^2 \theta - \tan^2 \theta = 1 \]
Substituting \( \theta = 23^\circ \):
\[ 1 + 2 = 2 \]
\begin{quicktipbox
The identity:
\[ \sec^2 \theta - \tan^2 \theta = 1 \]
is useful for solving such problems.
\end{quicktipbox Quick Tip: The identity: \[ \sec^2 \theta - \tan^2 \theta = 1 \] is useful for solving such problems.
If \( x \cos \theta = 1 \), \( \tan \theta = y \), then the value of \( x^2 - y^2 \) is:
View Solution
Given:
\[ x = \frac{1}{\cos \theta}, \quad y = \tan \theta = \frac{\sin \theta}{\cos \theta} \]
We need to find:
\[ x^2 - y^2 \]
Substituting:
\[ \frac{1}{\cos^2 \theta} - \frac{\sin^2 \theta}{\cos^2 \theta} \]
\[ = \frac{1 - \sin^2 \theta}{\cos^2 \theta} = \frac{\cos^2 \theta}{\cos^2 \theta} = 1 \]
\begin{quicktipbox
Using Pythagoras identity:
\[ \sin^2 \theta + \cos^2 \theta = 1 \]
helps in solving such expressions.
\end{quicktipbox Quick Tip: Using Pythagoras identity: \[ \sin^2 \theta + \cos^2 \theta = 1 \] helps in solving such expressions.
If \( \tan \theta = \frac{3}{4} \), then \( \sin \theta \) is:
View Solution
Using Pythagoras theorem, for \( \tan \theta = \frac{3}{4} \):
\[ Hypotenuse = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
\[ \sin \theta = \frac{opposite}{hypotenuse} = \frac{3}{5} \]
\begin{quicktipbox
For right-angled triangles, always use Pythagoras theorem to find missing sides.
\end{quicktipbox Quick Tip: For right-angled triangles, always use Pythagoras theorem to find missing sides.
\( \frac{1 + \cos A}{1 - \cos A} \) is equal to:
View Solution
Using trigonometric identity:
\[ \frac{1 + \cos A}{1 - \cos A} = \csc A + \cot A \]
This can be derived by expressing in terms of sine.
\begin{quicktipbox
Memorizing standard trigonometric formulas helps in quick solving.
\end{quicktipbox Quick Tip: Memorizing standard trigonometric formulas helps in quick solving.
\( \tan 5^\circ \cdot \tan 25^\circ \cdot \tan 30^\circ \cdot \tan 65^\circ \cdot \tan 85^\circ \) is:
View Solution
Using the property:
\[ \tan x \cdot \tan (90^\circ - x) = 1 \]
Pairing the terms:
\[ \tan 5^\circ \cdot \tan 85^\circ = 1 \]
\[ \tan 25^\circ \cdot \tan 65^\circ = 1 \]
And \( \tan 30^\circ = \frac{1}{\sqrt{3}} \).
Thus:
\[ 1 \times 1 \times \frac{1}{\sqrt{3}} \times \sqrt{3} = 1 \]
\begin{quicktipbox
The identity \( \tan x \cdot \tan (90^\circ - x) = 1 \) is useful for such problems.
\end{quicktipbox Quick Tip: The identity \( \tan x \cdot \tan (90^\circ - x) = 1 \) is useful for such problems.
\( \cos 38^\circ \cos 52^\circ - \sin 38^\circ \sin 52^\circ \) is:
View Solution
Using the trigonometric identity:
\[ \cos(A + B) = \cos A \cos B - \sin A \sin B \]
Substituting \( A = 38^\circ \), \( B = 52^\circ \):
\[ \cos(38^\circ + 52^\circ) = \cos 90^\circ = 1 \]
\begin{quicktipbox
The identity:
\[ \cos(A + B) = \cos A \cos B - \sin A \sin B \]
is useful for sum and difference trigonometry problems.
\end{quicktipbox Quick Tip: The identity: \[ \cos(A + B) = \cos A \cos B - \sin A \sin B \] is useful for sum and difference trigonometry problems.
\( \frac{\csc 42^\circ \cdot \cos 37^\circ}{\sec 48^\circ \cdot \sin 53^\circ} \) is:
View Solution
Using trigonometric identities:
\[ \csc 42^\circ = \frac{1}{\sin 42^\circ}, \quad \sec 48^\circ = \frac{1}{\cos 48^\circ} \]
\[ \cos 37^\circ = \sin 53^\circ \]
So,
\[ \frac{\frac{1}{\sin 42^\circ} \cdot \cos 37^\circ}{\frac{1}{\cos 48^\circ} \cdot \sin 53^\circ} \]
\[ = \frac{\cos 37^\circ}{\sin 42^\circ} \times \frac{\cos 48^\circ}{\sin 53^\circ} \]
Approximating values,
\[ = \frac{1}{2} \]
\begin{quicktipbox
Using reciprocal trigonometric identities simplifies the fraction.
\end{quicktipbox Quick Tip: Using reciprocal trigonometric identities simplifies the fraction.
If \( \tan(\alpha + \beta) = \sqrt{3} \) and \( \tan \alpha = \frac{1}{\sqrt{3}} \), then the value of \( \tan \beta \) is:
View Solution
Using tan sum formula:
\[ \tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \]
Substituting values:
\[ \sqrt{3} = \frac{\frac{1}{\sqrt{3}} + \tan \beta}{1 - \frac{1}{\sqrt{3}} \cdot \tan \beta} \]
Solving for \( \tan \beta \):
\[ \tan \beta = \frac{7}{6} \]
\begin{quicktipbox
Use the tan sum formula to solve such problems.
\end{quicktipbox Quick Tip: Use the tan sum formula to solve such problems.
\( \sqrt{2} \left(\sin \frac{\pi}{4} + \cos \frac{\pi}{4} \right) \) is:
View Solution
Since \( \sin \frac{\pi}{4} = \cos \frac{\pi}{4} = \frac{1}{\sqrt{2}} \):
\[ \sin \frac{\pi}{4} + \cos \frac{\pi}{4} = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} = \sqrt{2} \]
\[ \sqrt{2} \times \sqrt{2} = 2 \]
\begin{quicktipbox
Remember trigonometric values of standard angles for quick calculations.
\end{quicktipbox Quick Tip: Remember trigonometric values of standard angles for quick calculations.
If \( a \cos \theta + b \sin \theta = 4 \) and \( a \sin \theta - b \cos \theta = 3 \), then the value of \( a^2 + b^2 \) is:
View Solution
Squaring both equations and adding:
\[ (a \cos \theta + b \sin \theta)^2 + (a \sin \theta - b \cos \theta)^2 = 4^2 + 3^2 \]
\[ a^2 \cos^2 \theta + 2ab \cos \theta \sin \theta + b^2 \sin^2 \theta + a^2 \sin^2 \theta - 2ab \sin \theta \cos \theta + b^2 \cos^2 \theta = 16 + 9 \]
\[ a^2 (\cos^2 \theta + \sin^2 \theta) + b^2 (\sin^2 \theta + \cos^2 \theta) = 25 \]
Since \( \cos^2 \theta + \sin^2 \theta = 1 \):
\[ a^2 + b^2 = 25 \]
\begin{quicktipbox
Using the identity:
\[ \cos^2 \theta + \sin^2 \theta = 1 \]
simplifies such expressions.
\end{quicktipbox Quick Tip: Using the identity: \[ \cos^2 \theta + \sin^2 \theta = 1 \] simplifies such expressions.
The ratio of the areas of two circles is \( x^2 : y^2 \). Then the ratio of their radii is:
View Solution
The area of a circle is given by:
\[ A = \pi r^2 \]
If \( A_1 : A_2 = x^2 : y^2 \), then:
\[ \frac{\pi r_1^2}{\pi r_2^2} = \frac{x^2}{y^2} \]
Taking the square root:
\[ \frac{r_1}{r_2} = \frac{x}{y} \]
\begin{quicktipbox
The ratio of the areas of two circles is the square of the ratio of their radii.
\end{quicktipbox Quick Tip: The ratio of the areas of two circles is the square of the ratio of their radii.
The area of a circle is \( 49\pi \) square cm. Then its diameter is:
View Solution
The area of a circle is given by:
\[ A = \pi r^2 \]
\[ 49\pi = \pi r^2 \]
Dividing by \( \pi \):
\[ r^2 = 49 \]
\[ r = 7 cm \]
Since the diameter is:
\[ D = 2r = 2 \times 7 = 14 cm \]
\begin{quicktipbox
The diameter of a circle is always twice the radius.
\end{quicktipbox Quick Tip: The diameter of a circle is always twice the radius.
The distance covered by a wheel of radius 14 cm in 5 revolutions is:
View Solution
The distance covered in one revolution is the circumference:
\[ C = 2\pi r = 2\pi (14) = 28\pi \]
For 5 revolutions:
\[ Total Distance = 5 \times 28\pi = 140\pi \]
Approximating \( \pi \approx 3.14 \):
\[ 140 \times 3.14 = 439.6 \approx 440 cm \]
\begin{quicktipbox
The distance covered by a rolling wheel in one revolution is equal to its circumference.
\end{quicktipbox Quick Tip: The distance covered by a rolling wheel in one revolution is equal to its circumference.
If the area of a circle is equal to the area of a square, then the ratio of their perimeters is:
View Solution
Let the radius of the circle be \( r \) and the side of the square be \( s \).
\[ \pi r^2 = s^2 \]
\[ s = \sqrt{\pi r^2} = r\sqrt{\pi} \]
Perimeter of Circle:
\[ P_C = 2\pi r \]
Perimeter of Square:
\[ P_S = 4s = 4r\sqrt{\pi} \]
Taking the ratio:
\[ \frac{P_C}{P_S} = \frac{2\pi r}{4r\sqrt{\pi}} = \frac{\pi}{2} \]
\begin{quicktipbox
When comparing perimeters or areas, always express both in terms of the same variable.
\end{quicktipbox Quick Tip: When comparing perimeters or areas, always express both in terms of the same variable.
If \( p(x) = x^4 - 5x + 6 \) and \( q(x) = 2 - x^2 \), then the degree of \( \frac{p(x)}{q(x)} \) is:
View Solution
The degree of a fraction of polynomials is:
\[ Degree of \frac{p(x)}{q(x)} = Degree of p(x) - Degree of q(x) \]
Since:
\[ \deg(p(x)) = 4, \quad \deg(q(x)) = 2 \]
\[ \deg\left(\frac{p(x)}{q(x)}\right) = 4 - 2 = 2 \]
\begin{quicktipbox
For rational functions:
\[ \deg \left( \frac{p(x)}{q(x)} \right) = \deg p(x) - \deg q(x) \]
\end{quicktipbox Quick Tip: For rational functions: \[ \deg \left( \frac{p(x)}{q(x)} \right) = \deg p(x) - \deg q(x) \]
Which of the following is a quadratic equation?
View Solution
A quadratic equation is in the form:
\[ ax^2 + bx + c = 0, \quad where a \neq 0. \]
Expanding (D):
\[ 2x^2 - 5x = x^2 - 2x + 1 \]
\[ 2x^2 - 5x - x^2 + 2x - 1 = 0 \]
\[ x^2 - 3x - 1 = 0 \]
which is a quadratic equation.
\begin{quicktipbox
A quadratic equation must have the highest exponent of \( x \) as 2.
\end{quicktipbox Quick Tip: A quadratic equation must have the highest exponent of \( x \) as 2.
If one root of the quadratic equation \( x^2 + 2kx + 4 = 0 \) is \( 2 \), then the value of \( k \) is:
View Solution
Substituting \( x = 2 \) in the equation:
\[ 2^2 + 2k(2) + 4 = 0 \]
\[ 4 + 4k + 4 = 0 \]
\[ 8 + 4k = 0 \]
\[ 4k = -8 \]
\[ k = -2 \]
\begin{quicktipbox
If a root is given, substitute it in the quadratic equation and solve for the unknown.
\end{quicktipbox Quick Tip: If a root is given, substitute it in the quadratic equation and solve for the unknown.
If \( (x + 3) \) is a factor of \( ax^2 + x + 1 \), then the value of \( a \) is:
View Solution
Since \( (x + 3) \) is a factor, it must satisfy the equation:
\[ a(-3)^2 + (-3) + 1 = 0 \]
\[ 9a - 3 + 1 = 0 \]
\[ 9a - 2 = 0 \]
\[ 9a = 2 \]
\[ a = \frac{9}{2} \]
\begin{quicktipbox
If \( (x + p) \) is a factor, substitute \( x = -p \) and solve for unknowns.
\end{quicktipbox Quick Tip: If \( (x + p) \) is a factor, substitute \( x = -p \) and solve for unknowns.
For what value of \( p \) will the equation \( px^2 - 2x + 3 = 0 \) have real and equal roots?
View Solution
For real and equal roots, the discriminant must be zero:
\[ D = b^2 - 4ac = 0 \]
Here,
\[ b = -2, \quad a = p, \quad c = 3 \]
\[ (-2)^2 - 4(p)(3) = 0 \]
\[ 4 - 12p = 0 \]
\[ 12p = 4 \]
\[ p = \frac{1}{3} \]
\begin{quicktipbox
For a quadratic equation to have real and equal roots, the discriminant must be zero:
\[ b^2 - 4ac = 0 \]
\end{quicktipbox Quick Tip: For a quadratic equation to have real and equal roots, the discriminant must be zero: \[ b^2 - 4ac = 0 \]
What is the nature of roots of the quadratic equation \( 6x^2 - 3x + 5 = 0 \)?
View Solution
The nature of roots is determined using the discriminant:
\[ D = b^2 - 4ac \]
For \( 6x^2 - 3x + 5 = 0 \):
\[ D = (-3)^2 - 4(6)(5) = 9 - 120 = -111 \]
Since \( D < 0 \), the roots are not real.
\begin{quicktipbox
If \( D > 0 \), roots are real and unequal.
If \( D = 0 \), roots are real and equal.
If \( D < 0 \), roots are not real.
\end{quicktipbox Quick Tip: If \( D > 0 \), roots are real and unequal. If \( D = 0 \), roots are real and equal. If \( D < 0 \), roots are not real.
If one root of the quadratic equation \( x^2 + x - 20 = 0 \) is \( 4 \), then the other root is:
View Solution
Using the sum and product of roots formula:
\[ \alpha + \beta = -\frac{b}{a}, \quad \alpha \beta = \frac{c}{a} \]
For \( x^2 + x - 20 = 0 \):
\[ \alpha + \beta = -\frac{1}{1} = -1, \quad \alpha \beta = \frac{-20}{1} = -20 \]
Since one root is \( 4 \):
\[ 4 + \beta = -1 \]
\[ \beta = -5 \]
\begin{quicktipbox
Use the sum and product of roots:
\[ \alpha + \beta = -\frac{b}{a}, \quad \alpha \beta = \frac{c}{a} \]
\end{quicktipbox Quick Tip: Use the sum and product of roots: \[ \alpha + \beta = -\frac{b}{a}, \quad \alpha \beta = \frac{c}{a} \]
If \( \alpha \) and \( \beta \) are the roots of the quadratic equation \( x^2 + 6x + 5 = 0 \), then the value of \( \alpha^2 + \beta^2 \) is:
View Solution
Using the identity:
\[ \alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta \]
For \( x^2 + 6x + 5 = 0 \):
\[ \alpha + \beta = -6, \quad \alpha \beta = 5 \]
\[ \alpha^2 + \beta^2 = (-6)^2 - 2(5) = 36 - 10 = 26 \]
\begin{quicktipbox
The identity:
\[ \alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta \]
is useful in quadratic problems.
\end{quicktipbox Quick Tip: The identity: \[ \alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta \] is useful in quadratic problems.
The roots of the quadratic equation \( px^2 - qx + r = 0, \, p \neq 0 \) are:
View Solution
Using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
For \( px^2 - qx + r = 0 \):
\[ x = \frac{-(-q) \pm \sqrt{(-q)^2 - 4(p)(r)}}{2p} \]
\[ x = \frac{q \pm \sqrt{q^2 - 4pr}}{2p} \]
\begin{quicktipbox
The quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
is used to find roots of any quadratic equation.
\end{quicktipbox Quick Tip: The quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] is used to find roots of any quadratic equation.
If \( x = -1 \) is a common root of both the equations \( 2x^2 + 3x + p = 0 \) and \( qx^2 - qx + 4 = 0 \), then the value of \( p + q \) is:
View Solution
Since \( x = -1 \) is a root of both equations, substituting \( x = -1 \):
For \( 2(-1)^2 + 3(-1) + p = 0 \):
\[ 2 - 3 + p = 0 \Rightarrow p = 1 \]
For \( q(-1)^2 - q(-1) + 4 = 0 \):
\[ q + q + 4 = 0 \Rightarrow 2q = -4 \Rightarrow q = -2 \]
Thus:
\[ p + q = 1 + (-2) = -1 \]
\begin{quicktipbox
If a common root is given, substitute it into both equations and solve for unknowns.
\end{quicktipbox Quick Tip: If a common root is given, substitute it into both equations and solve for unknowns.
The length, breadth, and height of a cuboid are 15 m, 6 m, and 5 m, respectively. Then the lateral surface area of the cuboid is:
View Solution
The lateral surface area (LSA) of a cuboid is given by:
\[ LSA = 2h(l + b) \]
Substituting values:
\[ LSA = 2(5)(15 + 6) \]
\[ = 2(5)(21) = 210 m^2 \]
\begin{quicktipbox
The lateral surface area of a cuboid is given by:
\[ LSA = 2h(l + b) \]
where \( l, b, h \) are the length, breadth, and height.
\end{quicktipbox Quick Tip: The lateral surface area of a cuboid is given by: \[ LSA = 2h(l + b) \] where \( l, b, h \) are the length, breadth, and height.
How many cubes of side 4 cm can be formed from a cube of side 8 cm?
View Solution
The volume of a cube is:
\[ V = side^3 \]
For a cube of side 8 cm:
\[ V_1 = 8^3 = 512 cm^3 \]
For a cube of side 4 cm:
\[ V_2 = 4^3 = 64 cm^3 \]
Number of smaller cubes:
\[ N = \frac{V_1}{V_2} = \frac{512}{64} = 8 \]
\begin{quicktipbox
The number of smaller cubes from a larger cube is given by:
\[ N = \frac{Volume of Larger Cube}{Volume of Smaller Cube} \]
\end{quicktipbox Quick Tip: The number of smaller cubes from a larger cube is given by:
\[ N = \frac{Volume of Larger Cube}{Volume of Smaller Cube} \]
Three cubes of metal with edges 3 cm, 4 cm, and 5 cm respectively are melted to form a single cube. What is the lateral surface area of the new formed cube?
View Solution
Total volume of the three cubes:
\[ V = 3^3 + 4^3 + 5^3 = 27 + 64 + 125 = 216 \]
New cube's side:
\[ s = \sqrt[3]{216} = 6 cm \]
Lateral surface area of the new cube:
\[ LSA = 4s^2 = 4(6)^2 = 144 cm^2 \]
\begin{quicktipbox
When combining cubes, sum their volumes, then find the new side and compute the area.
\end{quicktipbox Quick Tip: When combining cubes, sum their volumes, then find the new side and compute the area.
The radii of two cylinders are in the ratio 2:3 and their heights are in the ratio 5:3. The ratio of their volumes is:
View Solution
The volume of a cylinder is:
\[ V = \pi r^2 h \]
Let the radii be \( 2x \) and \( 3x \), and the heights be \( 5y \) and \( 3y \).
\[ \frac{V_1}{V_2} = \frac{\pi (2x)^2 (5y)}{\pi (3x)^2 (3y)} \]
\[ = \frac{4x^2 \cdot 5y}{9x^2 \cdot 3y} = \frac{20}{27} \]
\begin{quicktipbox
For similar cylinders, the volume ratio is:
\[ \frac{V_1}{V_2} = \frac{r_1^2 h_1}{r_2^2 h_2} \]
\end{quicktipbox Quick Tip: For similar cylinders, the volume ratio is: \[ \frac{V_1}{V_2} = \frac{r_1^2 h_1}{r_2^2 h_2} \]
If the curved surface area of a cylinder is \( 1760 \) cm\(^2\) and its base radius is \( 14 \) cm, then its height is:
View Solution
Curved surface area of a cylinder:
\[ CSA = 2\pi rh \]
\[ 1760 = 2\pi (14) h \]
\[ 1760 = 2(3.14)(14) h \]
\[ 1760 = 87.92 h \]
\[ h = \frac{1760}{87.92} \approx 20 cm \]
\begin{quicktipbox
For cylinders, Curved Surface Area formula:
\[ CSA = 2\pi rh \]
\end{quicktipbox Quick Tip: For cylinders, Curved Surface Area formula:
\[ CSA = 2\pi rh \]
The external radius of a pipe of metal is \( 4 \) cm and internal radius is \( 3 \) cm. If its length is \( 10 \) cm, then the volume of metal is:
View Solution
Volume of a cylindrical pipe is given by:
\[ V = \pi h (R^2 - r^2) \]
\[ V = 3.14 \times 10 \times (4^2 - 3^2) \]
\[ V = 3.14 \times 10 \times (16 - 9) \]
\[ V = 3.14 \times 10 \times 7 \]
\[ V \approx 220 cm^3 \]
\begin{quicktipbox
For hollow cylinders, volume is:
\[ V = \pi h (R^2 - r^2) \]
\end{quicktipbox Quick Tip: For hollow cylinders, volume is: \[ V = \pi h (R^2 - r^2) \]
If \( r \) is the radius of the base of a cone and \( l \) is its slant height, then the curved surface area of the cone is:
View Solution
Curved surface area of a cone:
\[ CSA = \pi r l \]
\begin{quicktipbox
For cones, Curved Surface Area formula: \[ CSA = \pi r l \]
\end{quicktipbox Quick Tip: For cones, Curved Surface Area formula: \[ CSA = \pi r l \]
The total surface area of a hemisphere of diameter \( 14 \) cm is:
View Solution
The total surface area (TSA) of a hemisphere is:
\[ TSA = 3\pi r^2 \]
Given the diameter \( d = 14 \) cm, so radius:
\[ r = \frac{14}{2} = 7 cm \]
\[ TSA = 3\pi (7)^2 = 3\pi (49) = 147\pi \]
Since the total surface area includes the circular base:
\[ TSA = 147\pi + 49\pi = 198\pi cm^2 \]
\begin{quicktipbox
For hemispheres, the total surface area is:
\[ TSA = 3\pi r^2 \]
and the curved surface area is:
\[ CSA = 2\pi r^2 \]
\end{quicktipbox Quick Tip: For hemispheres, the total surface area is: \[ TSA = 3\pi r^2 \] and the curved surface area is: \[ CSA = 2\pi r^2 \]
The volume of a cone is \( 1570 \) cm\(^3\). If the area of its base is \( 314 \) cm\(^2\), then its height is:
View Solution
The volume of a cone is given by:
\[ V = \frac{1}{3} \pi r^2 h \]
Given:
\[ V = 1570, \quad Base Area = \pi r^2 = 314 \]
Rewriting the formula:
\[ h = \frac{3V}{\pi r^2} \]
Substituting values:
\[ h = \frac{3(1570)}{314} \]
\[ h = \frac{4710}{314} = 10 cm \]
\begin{quicktipbox
For cones, the volume formula is:
\[ V = \frac{1}{3} \pi r^2 h \]
To find height:
\[ h = \frac{3V}{\pi r^2} \]
\end{quicktipbox Quick Tip: For cones, the volume formula is: \[ V = \frac{1}{3} \pi r^2 h \] To find height: \[ h = \frac{3V}{\pi r^2} \]
If \( 2r \) is the radius of a sphere, then its volume is:
View Solution
The volume of a sphere is given by:
\[ V = \frac{4}{3} \pi R^3 \]
Since \( 2r \) is the radius, we substitute \( R = 2r \):
\[ V = \frac{4}{3} \pi (2r)^3 \]
\[ = \frac{4}{3} \pi (8r^3) = \frac{32\pi r^3}{3} \]
\begin{quicktipbox
For a sphere, the volume formula is:
\[ V = \frac{4}{3} \pi R^3 \]
\end{quicktipbox Quick Tip: For a sphere, the volume formula is: \[ V = \frac{4}{3} \pi R^3 \]
What is the 11th term of the A.P. \( -3, -\frac{1}{2}, 2, \dots \) ?
View Solution
The \( n \)th term of an arithmetic progression is:
\[ a_n = a + (n-1)d \]
Here, \( a = -3 \), \( d = -\frac{1}{2} - (-3) = \frac{5}{2} \), \( n = 11 \):
\[ a_{11} = -3 + (11-1) \times \frac{5}{2} \]
\[ = -3 + 10 \times \frac{5}{2} = -3 + 25 = 28 \]
\begin{quicktipbox
For an arithmetic sequence, the nth term formula is:
\[ a_n = a + (n-1)d \]
\end{quicktipbox Quick Tip:
For an arithmetic sequence, the nth term formula is: \[ a_n = a + (n-1)d \]
The number of terms in A.P. \( 41, 38, 35, \dots, 8 \) is:
View Solution
For an arithmetic sequence, we use:
\[ a_n = a + (n-1)d \]
Given \( a = 41 \), \( d = 38 - 41 = -3 \), and last term \( a_n = 8 \):
\[ 8 = 41 + (n-1)(-3) \]
\[ 8 - 41 = -3(n-1) \]
\[ -33 = -3(n-1) \]
\[ n-1 = 11 \]
\[ n = 14 \]
\begin{quicktipbox
To find the number of terms, solve for \( n \) using:
\[ a_n = a + (n-1)d \]
\end{quicktipbox Quick Tip: To find the number of terms, solve for \( n \) using: \[ a_n = a + (n-1)d \]
The sum of first 50 terms of the A.P. \( 2, 4, 6, 8, \dots \) is:
View Solution
The sum of the first \( n \) terms of an arithmetic progression is given by:
\[ S_n = \frac{n}{2} (2a + (n-1)d) \]
Here, \( a = 2 \), \( d = 4 - 2 = 2 \), and \( n = 50 \):
\[ S_{50} = \frac{50}{2} (2(2) + (50-1) \cdot 2) \]
\[ = 25 (4 + 98) = 25 \times 102 = 2550 \]
\begin{quicktipbox
For the sum of an arithmetic sequence:
\[ S_n = \frac{n}{2} (2a + (n-1)d) \]
\end{quicktipbox Quick Tip: For the sum of an arithmetic sequence: \[ S_n = \frac{n}{2} (2a + (n-1)d) \]
The point \( (2\sqrt{7}, -3) \) lies in which quadrant?
View Solution
The quadrants are defined as:
1. First Quadrant: \( (+, +) \)
2. Second Quadrant: \( (-, +) \)
3. Third Quadrant: \( (-, -) \)
4. Fourth Quadrant: \( (+, -) \)
Given \( (2\sqrt{7}, -3) \), since \( x > 0 \) and \( y < 0 \), it lies in the fourth quadrant.
\begin{quicktipbox
The sign of coordinates determines the quadrant:
- First Quadrant: \( (+, +) \)
- Second Quadrant: \( (-, +) \)
- Third Quadrant: \( (-, -) \)
- Fourth Quadrant: \( (+, -) \)
\end{quicktipbox Quick Tip: The sign of coordinates determines the quadrant: - First Quadrant: \( (+, +) \) - Second Quadrant: \( (-, +) \) - Third Quadrant: \( (-, -) \) - Fourth Quadrant: \( (+, -) \)
The distance between the points \( (2\cos \theta, 0) \) and \( (0, 2\sin \theta) \) is:
View Solution
The distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Substituting \( (x_1, y_1) = (2\cos \theta, 0) \) and \( (x_2, y_2) = (0, 2\sin \theta) \):
\[ d = \sqrt{(0 - 2\cos \theta)^2 + (2\sin \theta - 0)^2} \]
\[ = \sqrt{4\cos^2 \theta + 4\sin^2 \theta} \]
\[ = \sqrt{4(\cos^2 \theta + \sin^2 \theta)} \]
\[ = \sqrt{4 \times 1} = \sqrt{4} = 2 \]
\begin{quicktipbox
Use the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
\end{quicktipbox Quick Tip: Use the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
The intersecting point of straight lines \( x = -2 \) and \( y = 3 \) is:
View Solution
The equation \( x = -2 \) represents a vertical line passing through \( x = -2 \).
The equation \( y = 3 \) represents a horizontal line passing through \( y = 3 \).
The intersection occurs where both equations are satisfied, which is:
\[ (-2,3) \]
\begin{quicktipbox
For two perpendicular lines \( x = a \) and \( y = b \), the intersection point is \( (a, b) \).
\end{quicktipbox Quick Tip: For two perpendicular lines \( x = a \) and \( y = b \), the intersection point is \( (a, b) \).
The distance between the points \( (7, -4) \) and \( (-5,1) \) is:
View Solution
The distance formula between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Substituting \( (x_1, y_1) = (7, -4) \) and \( (x_2, y_2) = (-5, 1) \):
\[ d = \sqrt{(-5 - 7)^2 + (1 + 4)^2} \]
\[ = \sqrt{(-12)^2 + (5)^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \]
\begin{quicktipbox
The distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
is used to find the distance between two points.
\end{quicktipbox Quick Tip: The distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] is used to find the distance between two points.
The point on \( y \)-axis which is equidistant from the points \( (5, -2) \) and \( (-3,2) \) is:
View Solution
Let the required point on the y-axis be \( (0, y) \).
Since it is equidistant from \( (5, -2) \) and \( (-3,2) \), we use the distance formula:
\[ \sqrt{(0 - 5)^2 + (y + 2)^2} = \sqrt{(0 + 3)^2 + (y - 2)^2} \]
Squaring both sides:
\[ (5)^2 + (y+2)^2 = (3)^2 + (y-2)^2 \]
\[ 25 + y^2 + 4y + 4 = 9 + y^2 - 4y + 4 \]
Cancel \( y^2 \) and simplify:
\[ 25 + 4y + 4 = 9 - 4y + 4 \]
\[ 29 + 4y = 13 - 4y \]
\[ 8y = -16 \]
\[ y = -2 \]
So the point is \( (0,-2) \).
\begin{quicktipbox
For points on the y-axis, their x-coordinate is always 0.
Solve using the distance formula and equate both distances.
\end{quicktipbox Quick Tip: For points on the y-axis, their x-coordinate is always 0. Solve using the distance formula and equate both distances.
PQRS is a rectangle whose vertices are \( P(0,0) \), \( Q(6,0) \), \( R(6,2) \) and \( S(0,2) \). The area of the rectangle is:
View Solution
Step 1: The formula for the area of a rectangle is:
\[ Area = Length \times Breadth. \]
Step 2: Finding length and breadth:
\[ Length = |6 - 0| = 6, \quad Breadth = |2 - 0| = 2. \]
Step 3: Computing area:
\[ Area = 6 \times 2 = 12. \] Quick Tip: For rectangles, use: - Length = Difference of x-coordinates of two adjacent vertices. - Breadth = Difference of y-coordinates of two adjacent vertices.
If \( A(a,0) \), \( B(0,0) \), and \( C(0,b) \) are the vertices of \( \triangle ABC \), then the area of \( \triangle ABC \) is:
View Solution
Step 1: Using the area formula for a triangle:
\[ Area = \frac{1}{2} \times Base \times Height. \]
Step 2: Identifying base and height:
\[ Base = a, \quad Height = b. \]
Step 3: Computing area:
\[ Area = \frac{1}{2} \times a \times b = \frac{1}{2} ab. \] Quick Tip: For right-angled triangles: - Base is the horizontal side. - Height is the vertical side.
Which of the following is not a polynomial?
View Solution
Step 1: A polynomial must have whole number exponents.
Step 2: Checking options:
- \( x^2 + \sqrt{5} \) is a polynomial (constant term can be an irrational number).
- \( 9x^2 - 4x + \sqrt{2} \) is also a polynomial.
- \( \frac{1}{2} x^3 + \frac{3}{5} x^2 + 8 \) is a polynomial.
- \( x + \frac{3}{x} \) is not a polynomial since \( x^{-1} \) is not a whole number.
Quick Tip: A polynomial must have: - Whole number exponents. - Finite number of terms.
The degree of the polynomial \( (x^5 + x^2 + 3x)(x^6 + x^5 + x^2 + 1) \) is:
View Solution
Step 1: The degree of a polynomial is the highest power of \( x \).
Step 2: Finding degrees:
\[ Degree of (x^5 + x^2 + 3x) = 5, \quad Degree of (x^6 + x^5 + x^2 + 1) = 6. \]
Step 3: The degree of the product is:
\[ 5 + 6 = 11. \] Quick Tip: For polynomial multiplication: - The highest degree term determines the overall degree. - The sum of the degrees of individual polynomials gives the final degree.
The zeroes of the polynomial \( x^2 - 11 \) are:
View Solution
Step 1: Setting the polynomial to zero:
\[ x^2 - 11 = 0. \]
Step 2: Solving for \( x \):
\[ x^2 = 11 \quad \Rightarrow \quad x = \pm\sqrt{11}. \] Quick Tip: To find the roots of \( x^2 - c = 0 \), take the square root: \[ x = \pm \sqrt{c}. \]
If -2 and -3 are the zeroes of the quadratic polynomial \( x^2 + (a+1)x + b \), then:
View Solution
Step 1: Using the sum and product of roots formula:
\[ \alpha + \beta = -\frac{Coefficient of x}{Coefficient of x^2} \] \[ \alpha \beta = \frac{Constant term}{Coefficient of x^2}. \]
Step 2: Substituting \( \alpha = -2 \), \( \beta = -3 \):
\[ (-2) + (-3) = - (a+1) \quad \Rightarrow \quad -5 = -a -1 \quad \Rightarrow \quad a = -2. \]
\[ (-2) \times (-3) = b \quad \Rightarrow \quad b = 6. \] Quick Tip: For quadratic equations \( ax^2 + bx + c = 0 \): \[ Sum of roots = -\frac{b}{a}, \quad Product of roots = \frac{c}{a}. \]
If the product of the zeroes of the polynomial \( x^2 - 9x + a \) is 8, then the value of \( a \) is:
View Solution
Step 1: The product of the zeroes of a quadratic polynomial \( ax^2 + bx + c \) is:
\[ \frac{c}{a}. \]
Step 2: Given the polynomial:
\[ x^2 - 9x + a = 0. \]
Here, the coefficient of \( x^2 \) is 1, so:
\[ Product of roots = \frac{a}{1} = a. \]
Step 3: Setting the equation:
\[ a = 8. \] Quick Tip: For a quadratic equation \( ax^2 + bx + c = 0 \), the product of roots is given by: \[ \frac{c}{a}. \]
Which of the following polynomial has roots 4 and -2?
View Solution
Step 1: The polynomial with given roots \( \alpha \) and \( \beta \) is:
\[ (x - \alpha)(x - \beta) = 0. \]
Step 2: Substituting \( \alpha = 4 \), \( \beta = -2 \):
\[ (x - 4)(x + 2) = 0. \]
Step 3: Expanding:
\[ x^2 + 2x - 4x - 8 = x^2 - 2x - 8. \] Quick Tip: The quadratic equation for given roots \( \alpha, \beta \) is: \[ (x - \alpha)(x - \beta) = 0. \]
If \( \alpha \) and \( \beta \) are the zeroes of the polynomial \( p(x) = x^2 + 3x - 4 \), then the value of \( \frac{\alpha \beta}{4} \) is:
View Solution
From the quadratic equation, the product of the roots is:
\[ \alpha \beta = c/a = \frac{-4}{1} = -4. \]
Thus, \[ \frac{\alpha \beta}{4} = \frac{-4}{4} = -1. \] Quick Tip: For a quadratic equation \( ax^2 + bx + c = 0 \), the roots satisfy: \[ \alpha + \beta = -\frac{b}{a}, \quad \alpha \beta = \frac{c}{a}. \]
If one zero of the polynomial \( q(x) \) is -3, then one factor of \( q(x) \) is:
View Solution
If \( x = -3 \) is a root, then \( (x + 3) \) must be a factor of \( q(x) \), because any polynomial having root \( r \) has a factor \( (x - r) \).
Quick Tip: If \( r \) is a root of a polynomial \( p(x) \), then \( (x - r) \) is always a factor of \( p(x) \).
If \( f(x) = x^4 - 2x^3 - x + 2 \) is divided by \( g(x) = x^2 - 3x + 2 \), then the degree of the quotient is:
View Solution
The degree of \( f(x) \) is 4 and the degree of \( g(x) \) is 2.
The degree of the quotient is given by:
\[ deg(f(x)) - deg(g(x)) = 4 - 2 = 2. \] Quick Tip: For polynomial division, the degree of the quotient is: \[ deg(f) - deg(g). \]
If \( \alpha \) and \( \beta \) are the zeroes of the polynomial \( x^2 - 3(x+1) - 5 \), then the value of \( (\alpha +1)(\beta +1) \) is:
View Solution
Expanding the given polynomial:
\[ x^2 - 3x - 3 - 5 = x^2 - 3x - 8. \]
Sum and product of roots:
\[ \alpha + \beta = -\left(\frac{-3}{1}\right) = 3, \quad \alpha \beta = \frac{-8}{1} = -8. \]
Now, we compute:
\[ (\alpha + 1)(\beta + 1) = \alpha \beta + \alpha + \beta + 1. \] \[ = (-8) + 3 + 1 + 1 = 4. \] Quick Tip: Use the identity: \[ (\alpha + k)(\beta + k) = \alpha\beta + k(\alpha + \beta) + k^2. \]
The mean of the first ten consecutive odd numbers is:
View Solution
The first ten odd numbers are:
\[ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. \]
The mean formula is:
\[ \frac{Sum of numbers}{Total numbers}. \]
Sum = \( 1 + 3 + 5 + \dots + 19 = 100 \),
so,
\[ Mean = \frac{100}{10} = 10. \] Quick Tip: For the first \( n \) odd numbers, the mean is always the middle term when \( n \) is odd, or the average of the two middle terms when \( n \) is even.
The median of 15, 6, 16, 8, 22, 21, 9, 18, 25 is:
View Solution
First, arrange the numbers in ascending order:
\[ 6, 8, 9, 15, 16, 18, 21, 22, 25. \]
Since there are 9 numbers (odd count), the median is the middle term:
\[ Median = 15. \] Quick Tip: For an odd number of values, the median is the middle term. For an even number of values, the median is the average of the two middle terms.
The mode of 0, 6, 5, 1, 6, 4, 3, 0, 2, 6, 5, 6 is:
View Solution
The mode is the number that appears most frequently.
Counting occurrences:
\[ 0(2), \quad 1(1), \quad 2(1), \quad 3(1), \quad 4(1), \quad 5(2), \quad 6(4). \]
Since 6 appears most frequently (4 times), the mode is:
\[ Mode = 6. \] Quick Tip: The mode is the most frequently occurring number in a data set.
If a class interval has a median class of 48-64 and mode class of 46-52, then its mean is:
View Solution
The empirical formula for mean, median, and mode is:
\[ Mean \approx \frac{Mode + 2(Median)}{3}. \]
Substituting:
\[ Mean \approx \frac{(49) + 2(50)}{3} = \frac{49 + 100}{3} = 50. \] Quick Tip: For grouped data, use the empirical relation: \[ Mean \approx \frac{Mode + 2(Median)}{3}. \]
If the mean of five observations \( x, x+2, x+4, x+6, x+8 \) is 11, then the value of \( x \) is:
View Solution
The mean formula is:
\[ \frac{Sum of observations}{Total observations}. \] \[ \frac{x + (x+2) + (x+4) + (x+6) + (x+8)}{5} = 11. \] \[ \frac{5x + 20}{5} = 11. \] \[ 5x + 20 = 55. \] \[ 5x = 35. \] \[ x = 7. \] Quick Tip: For an arithmetic sequence, the mean is the middle term if the sequence has an odd number of terms.
What is the probability of an impossible event?
View Solution
An impossible event means an event that cannot occur. The probability of such an event is always:
\[ P(E) = 0. \] Quick Tip: Probability ranges from 0 to 1. An impossible event has probability 0, and a certain event has probability 1.
If \( P(E) = 0.4 \), then the value of \( P(E') \) is:
View Solution
Since \( P(E) + P(E') = 1 \), we get: \[ P(E') = 1 - P(E) = 1 - 0.4 = 0.6. \] Quick Tip: The probability of the complement of an event is given by: \[ P(E') = 1 - P(E). \]
In the throw of two dice, the number of possible outcomes is:
View Solution
Each die has 6 faces. Since two dice are rolled together, the total number of possible outcomes is:
\[ 6 \times 6 = 36. \] Quick Tip: For multiple independent events, the total number of outcomes is the product of individual possibilities.
Which of the following numbers cannot be the probability of an event?
View Solution
Probability values range between 0 and 1. Since 1.5 is greater than 1, it cannot be a valid probability.
Quick Tip: A valid probability must be between 0 and 1 (inclusive).
What is the probability of not getting an odd number in a throw of a die once?
View Solution
A die has six numbers: \( 1, 2, 3, 4, 5, 6 \). The odd numbers are \( 1, 3, 5 \), and the even numbers are \( 2, 4, 6 \).
Since half of the numbers are even, the probability of not getting an odd number is:
\[ \frac{3}{6} = \frac{1}{2}. \] Quick Tip: For a fair die, each face has an equal probability of \( \frac{1}{6} \).
If \( 2a + 3b = 8 \) and \( 3a - 4b = -5 \), then the values of \( a \) and \( b \) are:
View Solution
We solve the system of equations:
\[ 2a + 3b = 8 \quad \cdots (1) \] \[ 3a - 4b = -5 \quad \cdots (2) \]
Step 1: Multiply equation (1) by 3 and equation (2) by 2 to align coefficients of \( a \):
\[ 6a + 9b = 24 \] \[ 6a - 8b = -10 \]
Step 2: Subtract the second equation from the first:
\[ (6a + 9b) - (6a - 8b) = 24 - (-10) \]
\[ 17b = 34 \]
\[ b = 2 \]
Step 3: Substitute \( b = 2 \) in equation (1):
\[ 2a + 3(2) = 8 \]
\[ 2a + 6 = 8 \]
\[ 2a = 2 \]
\[ a = 1 \]
Thus, \( a = 1, b = 2 \).
Quick Tip: For solving a system of linear equations, use the elimination or substitution method.
The pair of linear equations \( 2x - 3y = 8 \) and \( 4x - 6y = 9 \) are:
View Solution
Rewriting the equations:
\[ 2x - 3y = 8 \quad \cdots (1) \]
\[ 4x - 6y = 9 \quad \cdots (2) \]
Step 1: Multiply equation (1) by 2:
\[ 4x - 6y = 16 \]
Step 2: Compare with equation (2):
\[ 4x - 6y = 16 \quad (from equation 1) \]
\[ 4x - 6y = 9 \quad (original equation 2) \]
Since the left-hand sides are the same but the right-hand sides are different, the system is inconsistent and has no solution.
Quick Tip: A system of equations is inconsistent if the lines are parallel, meaning they have the same slope but different intercepts.
The graphs of the equations \( 2x + 3y = 4 \) and \( 4x + 6y = 12 \) are which type of straight lines?
View Solution
Rewriting the equations:
\[ 2x + 3y = 4 \quad \cdots (1) \] \[ 4x + 6y = 12 \quad \cdots (2) \]
Dividing equation (2) by 2:
\[ 2x + 3y = 6 \]
Comparing with equation (1):
\[ 2x + 3y = 4 \]
Since both equations have the same left-hand side but different constants on the right-hand side, they represent parallel lines.
Quick Tip: Two linear equations represent parallel lines if their slopes are equal but their constants differ.
How many solutions does the system of linear equations \( 2x - 3y + 1 = 0 \) and \( 3x + y + 2 = 0 \) have?
View Solution
Since the two equations have different slopes, they intersect at a single point, meaning the system has a unique solution.
Quick Tip: If two linear equations have different slopes, they have a unique solution.
For what value of \( k \), does the system of equations \( x + 2y = 3 \) and \( 5x + ky = 15 \) have infinite solutions?
View Solution
For infinite solutions, the two equations must be proportional:
\[ \frac{1}{5} = \frac{2}{k} = \frac{3}{15} \]
Solving for \( k \):
\[ k = \frac{2 \times 15}{5} = 6. \] Quick Tip: A system has infinite solutions when the two equations are scalar multiples of each other.
Which of the following is an arithmetic progression (A.P.)?
View Solution
An arithmetic progression (A.P.) has a constant common difference. Checking the differences:
\[ -4 - 0 = -4, \quad -8 - (-4) = -4, \quad -12 - (-8) = -4. \]
Since the common difference is constant (\( -4 \)), this sequence is an A.P.
Quick Tip: In an A.P., the difference between consecutive terms is always the same.
For what value of \( p \), do the terms \( (2p + 1), 13, (5p - 3) \) form an A.P.?
View Solution
For an A.P., the difference between consecutive terms must be equal:
\[ 13 - (2p + 1) = (5p - 3) - 13. \]
\[ 12 - 2p = 5p - 16. \]
Solving for \( p \):
\[ 12 + 16 = 5p + 2p. \]
\[ 28 = 7p. \]
\[ p = 6. \] Quick Tip: In an A.P., if three terms are given, use \( 2b = a + c \) to find missing variables.
If \( a_n \) is the \( n \)th term of A.P. \( 3, 8, 13, 18, \dots \), then what is the value of \( a_{25} - a_{10} \)?
View Solution
The general term of an arithmetic progression is given by:
\[ a_n = a + (n - 1)d. \]
Here, \( a = 3 \) and \( d = 8 - 3 = 5 \).
Finding \( a_{25} \):
\[ a_{25} = 3 + (25 - 1) \times 5 = 3 + 24 \times 5 = 3 + 120 = 123. \]
Finding \( a_{10} \):
\[ a_{10} = 3 + (10 - 1) \times 5 = 3 + 9 \times 5 = 3 + 45 = 48. \]
Now,
\[ a_{25} - a_{10} = 123 - 48 = 55. \] Quick Tip: The general formula for an arithmetic sequence is: \[ a_n = a + (n - 1)d. \]
The second term of an A.P. is 13 and its fifth term is 25. The common difference of the A.P. is:
View Solution
Using the formula:
\[ a_n = a + (n-1)d. \]
For the second term:
\[ a + d = 13 \quad \cdots (1). \]
For the fifth term:
\[ a + 4d = 25 \quad \cdots (2). \]
Subtracting equation (1) from equation (2):
\[ (a + 4d) - (a + d) = 25 - 13. \]
\[ 3d = 12. \]
\[ d = 4. \] Quick Tip: For finding the common difference \( d \), use: \[ d = \frac{a_m - a_n}{m - n}. \]
If the sum of the first \( n \) terms of an arithmetic sequence is given by \( S_n = 5n - n^2 \), then the common difference of the sequence is:
View Solution
We know that:
\[ a_n = S_n - S_{n-1}. \]
First term:
\[ a_1 = S_1 = 5(1) - (1)^2 = 5 - 1 = 4. \]
Second term:
\[ a_2 = S_2 - S_1. \]
\[ S_2 = 5(2) - (2)^2 = 10 - 4 = 6. \]
\[ a_2 = 6 - 4 = 2. \]
Common difference:
\[ d = a_2 - a_1 = 2 - 4 = -2. \] Quick Tip: To find the common difference from the sum formula, use: \[ d = a_2 - a_1. \]
\( \sqrt{\frac{64}{81}} + \sqrt{\frac{16}{9}} \) is:
View Solution
\[ \sqrt{\frac{64}{81}} + \sqrt{\frac{16}{9}} = \frac{\sqrt{64}}{\sqrt{81}} + \frac{\sqrt{16}}{\sqrt{9}}. \]
\[ = \frac{8}{9} + \frac{4}{3}. \]
Converting to a common denominator:
\[ = \frac{8}{9} + \frac{12}{9} = \frac{20}{9}. \]
Since \( 20/9 \) is not an integer, the correct answer is an integer only if there's a mistake in options.
Quick Tip: Simplify square roots in fractions separately before adding.
The product of two irrational numbers \( 3 + \sqrt{6} \) and \( 3 - \sqrt{5} \) will be a:
View Solution
\[ (3+\sqrt{6})(3-\sqrt{5}) = 3^2 - \sqrt{6} \cdot \sqrt{5}. \]
\[ = 9 - \sqrt{30}. \]
Since \( \sqrt{30} \) is irrational, \( 9 - \sqrt{30} \) remains irrational unless given differently.
Quick Tip: The product of two irrational numbers is not always irrational.
The simplest form of \( 0.\overline{3} + 0.\overline{4} \) is:
View Solution
Convert repeating decimals into fractions:
\[ 0.\overline{3} = \frac{1}{3}, \quad 0.\overline{4} = \frac{2}{5}. \]
Finding LCM of 3 and 5:
\[ \frac{5}{15} + \frac{6}{15} = \frac{7}{10}. \] Quick Tip: Convert repeating decimals to fractions using algebraic methods.
If \( 156 = 2^x \times 3^y \times 13^z \), then \( x + y + z = \)?
View Solution
Prime factorizing 156:
\[ 156 = 2^2 \times 3^1 \times 13^1. \]
\[ x = 2, \quad y = 1, \quad z = 1. \]
\[ x + y + z = 2 + 1 + 1 = 5. \] Quick Tip: Break numbers into prime factors to solve exponent equations.
\( \sqrt{10} \times \sqrt{15} \) is:
View Solution
\[ \sqrt{10} \times \sqrt{15} = \sqrt{10 \times 15} = \sqrt{150}. \]
Since \( \sqrt{150} \) is not a perfect square, it remains irrational.
Quick Tip: The product of two square roots is a square root of their product.
In the form of \( \frac{p}{2^n \times 5^m} \), 0.105 can be written as:
View Solution
\[ 0.105 = \frac{105}{1000} = \frac{21}{200}. \]
Prime factorizing the denominator:
\[ 200 = 2 \times 5^3. \]
Thus,
\[ 0.105 = \frac{21}{2 \times 5^3}. \] Quick Tip: Convert decimals to fractions and factorize the denominator.
If H.C.F. of two numbers is 25 and L.C.M is 50, then the product of numbers will be:
View Solution
The product of two numbers is given by:
\[ Product = HCF \times LCM. \]
\[ = 25 \times 50 = 1250. \] Quick Tip: The product of two numbers is always equal to the product of their HCF and LCM.
If in the division algorithm \( a = bq + r \), given \( b = 61 \), \( q = 27 \), and \( r = 32 \), then the value of \( a \) is:
View Solution
Using the division algorithm:
\[ a = bq + r. \]
\[ a = 61 \times 27 + 32. \]
\[ a = 1647 + 32 = 1679. \] Quick Tip: In the division algorithm \( a = bq + r \), \( r \) must always be smaller than \( b \).
If \( q \) is a positive integer, which of the following is an odd positive integer?
View Solution
An odd number is of the form \( 2k + 1 \).
Checking each option:
- \( 6q + 2 \) is even.
- \( 6q + 4 \) is even.
- \( 6q + 6 \) is even.
- \( 6q + 1 \) is always odd.
Thus, \( 6q + 1 \) is the correct choice.
Quick Tip: An even number is divisible by 2, while an odd number is of the form \( 2k+1 \).
The H.C.F. of two consecutive odd numbers is:
View Solution
Consecutive odd numbers do not share common factors other than 1.
\[ H.C.F. = 1. \] Quick Tip: Two consecutive odd numbers are always coprime.
Section-B
(Short Answer Type Questions)
Find the area of the triangle whose vertices are \( (0,4) \), \( (3,6) \), and \( (-8,-2) \).
View Solution
The area of a triangle given vertices \( (x_1, y_1) \), \( (x_2, y_2) \), and \( (x_3, y_3) \) is:
\[ A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|. \]
Substituting values:
\[ A = \frac{1}{2} \left| 0(6 + 2) + 3(-2 - 4) + (-8)(4 - 6) \right|. \]
\[ = \frac{1}{2} \left| 0 + 3(-6) + (-8)(-2) \right|. \]
\[ = \frac{1}{2} \left| -18 + 16 \right| = \frac{1}{2} \times 2 = 1. \] Quick Tip: Always take the absolute value when calculating area using determinants.
Evaluate: \( \csc 39^\circ \cos 51^\circ + \tan 21^\circ \cot 69^\circ - \sec^2 21^\circ \)
View Solution
Using trigonometric identities:
\[ \csc 39^\circ = \frac{1}{\sin 39^\circ}, \quad \cos 51^\circ = \sin 39^\circ. \]
\[ \csc 39^\circ \cos 51^\circ = \frac{1}{\sin 39^\circ} \times \sin 39^\circ = 1. \]
\[ \tan 21^\circ \cot 69^\circ = \tan 21^\circ \times \frac{1}{\tan 69^\circ}. \]
\[ = \tan 21^\circ \times \cot 69^\circ = 1. \]
\[ \sec^2 21^\circ = 1 + \tan^2 21^\circ. \]
Using approximate values:
\[ \sec^2 21^\circ \approx 1 + 0.14 = 1.14. \]
Thus,
\[ 1 + 1 - 1.14 = 0.86. \] Quick Tip: Use fundamental trigonometric identities to simplify expressions.
Prove that \( \sec^4 \theta - \tan^4 \theta = 1 + 2\tan^2 \theta \).
View Solution
We use the identity:
\[ \sec^2 \theta = 1 + \tan^2 \theta. \]
Expanding the given expression:
\[ \sec^4 \theta - \tan^4 \theta = (\sec^2 \theta + \tan^2 \theta)(\sec^2 \theta - \tan^2 \theta). \]
Since,
\[ \sec^2 \theta - \tan^2 \theta = 1. \]
\[ \sec^4 \theta - \tan^4 \theta = (\sec^2 \theta + \tan^2 \theta) \times 1. \]
\[ = \sec^2 \theta + \tan^2 \theta. \]
Using \( \sec^2 \theta = 1 + \tan^2 \theta \), we get:
\[ 1 + 2\tan^2 \theta. \] Quick Tip: Use algebraic identities like \( a^2 - b^2 = (a+b)(a-b) \) to simplify expressions.
Prove that \( (\sqrt{2} + 2)^2 \) is an irrational number.
View Solution
Step 1: Expanding the given expression
We expand the given square:
\[ (\sqrt{2} + 2)^2 = (\sqrt{2})^2 + 2(2)(\sqrt{2}) + 2^2 \] \[ = 2 + 4\sqrt{2} + 4 \] \[ = 6 + 4\sqrt{2} \]
Step 2: Checking rationality
- Here, \( 6 \) is a rational number.
- \( 4\sqrt{2} \) consists of the term \( \sqrt{2} \), which is an irrational number.
- The sum of a rational number and an irrational number is always irrational.
Step 3: Conclusion
Since \( 6 + 4\sqrt{2} \) contains an irrational component, it is irrational.
Thus, we have proved that \( (\sqrt{2} + 2)^2 \) is an irrational number.
Quick Tip: The sum or product of a rational number and an irrational number is always irrational. Expanding and identifying irrational components helps in proving irrationality.
Find the zeroes of the quadratic polynomial \( x^2 - 3 \) and verify the relationship between the zeroes and the coefficients.
View Solution
The given quadratic equation is:
\[ x^2 - 3 = 0. \]
Solving for \( x \):
\[ x = \pm \sqrt{3}. \]
Now, sum of the roots:
\[ \alpha + \beta = \sqrt{3} + (-\sqrt{3}) = 0. \]
Product of the roots:
\[ \alpha \beta = (\sqrt{3}) \times (-\sqrt{3}) = -3. \]
Comparing with the standard quadratic form \( ax^2 + bx + c = 0 \):
\[ Sum = -\frac{b}{a} = 0, \quad Product = \frac{c}{a} = -3. \]
The relationship holds.
Quick Tip: For quadratic polynomials \( ax^2 + bx + c \), sum of roots \( = -b/a \), product of roots \( = c/a \).
Divide polynomial \( x^4 - 2x^3 - x + 2 \) by the polynomial \( x^2 - 3x + 2 \).
View Solution
Perform polynomial division:
\[ \frac{x^4 - 2x^3 - x + 2}{x^2 - 3x + 2}. \]
Dividing the first term:
\[ \frac{x^4}{x^2} = x^2. \]
Multiply:
\[ x^2(x^2 - 3x + 2) = x^4 - 3x^3 + 2x^2. \]
Subtract:
\[ (-2x^3 - x + 2) - (-3x^3 + 2x^2) = x^3 - 2x^2 - x + 2. \]
Dividing the first term:
\[ \frac{x^3}{x^2} = x. \]
Multiply:
\[ x(x^2 - 3x + 2) = x^3 - 3x^2 + 2x. \]
Subtract:
\[ (-2x^2 - x + 2) - (-3x^2 + 2x) = x^2 - 3x + 2. \]
Divide:
\[ \frac{x^2}{x^2} = 1. \]
Multiply:
\[ 1(x^2 - 3x + 2) = x^2 - 3x + 2. \]
Subtract:
\[ (x^2 - 3x + 2) - (x^2 - 3x + 2) = 0. \]
Thus, the quotient is:
\[ x^2 + x + 1. \] Quick Tip: Use long division method carefully to divide polynomials step by step.
Using Euclid division algorithm, find the HCF of 252 and 594.
View Solution
Using Euclid’s algorithm:
\[ Step 1: Divide 594 by 252. \]
\[ 594 \div 252 = 2 remainder 90. \]
\[ Step 2: Divide 252 by 90. \]
\[ 252 \div 90 = 2 remainder 72. \]
\[ Step 3: Divide 90 by 72. \]
\[ 90 \div 72 = 1 remainder 18. \]
\[ Step 4: Divide 72 by 18. \]
\[ 72 \div 18 = 4 remainder 0. \]
Since remainder is 0, HCF = 18.
Quick Tip: Use the remainder repeatedly until it becomes zero to find HCF.
Find the mean of the following data:

View Solution
Mean is given by:
\[ \bar{x} = \frac{\sum f_i x_i}{\sum f_i}. \]
\[ \sum f_i x_i = (4 \times 4) + (6 \times 8) + (8 \times 14) + (10 \times 11) + (12 \times 3). \]
\[ = 16 + 48 + 112 + 110 + 36 = 322. \]
\[ \sum f_i = 4 + 8 + 14 + 11 + 3 = 40. \]
\[ \bar{x} = \frac{322}{40} = 8.05. \] Quick Tip: Multiply each value by its frequency, sum them, then divide by total frequency.
A circle has a radius of 6 cm. Find the length of that chord which is at a distance of 4 cm from the center.
View Solution
Using the perpendicular bisector theorem:
\[ L = 2\sqrt{r^2 - d^2}. \]
\[ L = 2\sqrt{6^2 - 4^2}. \]
\[ = 2\sqrt{36 - 16} = 2\sqrt{20} = 2 \times 2\sqrt{5} = 4\sqrt{5} \approx 8.94 cm. \] Quick Tip: Use Pythagoras theorem to find chord length when perpendicular from center is given.
If one zero of the polynomial \( (a+2)x^2 - 3ax -2 \) is negative of the other, then find the polynomial.
View Solution
Let the roots be \( \alpha \) and \( -\alpha \).
Sum of the roots:
\[ \alpha + (-\alpha) = 0 = -\frac{-3a}{a+2}. \]
\[ \Rightarrow \frac{3a}{a+2} = 0 \Rightarrow 3a = 0 \Rightarrow a = 0. \]
Thus, the polynomial simplifies to:
\[ (x^2 - c^2). \] Quick Tip: For opposite roots, sum of roots must be zero.
The sum of the digits of a two-digit number is 9. If 9 is added to the number, the digits of the number are reversed. Write the equation for these statements.
View Solution
Let the two-digit number be \( 10x + y \), where \( x \) and \( y \) are its digits.
Given:
\[ x + y = 9. \]
Also, when 9 is added, the digits reverse:
\[ 10x + y + 9 = 10y + x. \]
Rearrange:
\[ 10x + y + 9 - x - 10y = 0. \]
\[ 9x - 9y = -9. \]
Dividing by 9:
\[ x - y = -1. \]
Thus, the system of equations is:
\[ x + y = 9, \quad x - y = -1. \] Quick Tip: Define digits properly and form equations based on place values.
Solve the pair of equations \( \sqrt{2} x + \sqrt{3}y = 0 \) and \( \sqrt{3}x - \sqrt{8}y = 0 \) by the method of substitution or elimination.
View Solution
Using elimination, multiply the first equation by \( \sqrt{3} \) and the second by \( \sqrt{2} \):
\[ \sqrt{6} x + 3y = 0. \]
\[ \sqrt{6} x - 2\sqrt{2} y = 0. \]
Subtracting:
\[ (3y + 2\sqrt{2} y) = 0. \]
\[ y(3 + 2\sqrt{2}) = 0. \]
\[ y = 0. \]
Substituting in \( \sqrt{2} x + \sqrt{3} y = 0 \):
\[ \sqrt{2} x = 0 \Rightarrow x = 0. \]
\[ (x, y) = (0,0). \] Quick Tip: For equations with square roots, eliminate them by multiplying appropriately.
The length, breadth, and height of a cuboid are 26 m, 14 m, and 6.5 m, respectively. Find the lateral surface area of the cuboid.
View Solution
Lateral Surface Area (LSA) is given by:
\[ LSA = 2h(l + b). \]
\[ = 2 \times 6.5 (26 + 14). \]
\[ = 2 \times 6.5 \times 40 = 520 m^2. \] Quick Tip: Lateral surface area covers only the sides, not the top and bottom.
The curved surface area and volume of a cylinder are 264 m\(^2\) and 396 m\(^3\) respectively. Find the radius and height of the cylinder.
View Solution
Curved Surface Area (CSA) of a cylinder:
\[ 2\pi rh = 264. \]
Volume of a cylinder:
\[ \pi r^2 h = 396. \]
Dividing:
\[ \frac{2\pi rh}{\pi r^2 h} = \frac{264}{396}. \]
\[ \frac{2}{r} = \frac{2}{3}. \]
\[ r = 3. \]
Substituting in \( 2\pi rh = 264 \):
\[ 2\pi (3)h = 264. \]
\[ 6\pi h = 264. \]
\[ h = \frac{264}{6\pi} = 14. \] Quick Tip: Divide volume by CSA to simplify the radius-height relationship.
The base radius of a cone is \( 7\sqrt{7} \) cm and its height is 21 cm. Find the volume of the cone.
View Solution
Volume of a cone:
\[ V = \frac{1}{3} \pi r^2 h. \]
\[ = \frac{1}{3} \pi (7\sqrt{7})^2 \times 21. \]
\[ = \frac{1}{3} \pi (49 \times 7) \times 21. \]
\[ = \frac{1}{3} \pi (343 \times 21). \]
\[ = \frac{1}{3} \pi (7203). \]
\[ = 2401\pi cm^3. \] Quick Tip: Use the formula \( V = \frac{1}{3} \pi r^2 h \) for cones.
If the sum of the first 14 terms of an A.P. is 1050 and its first term is 10, find the 20th term.
View Solution
Sum of an A.P:
\[ S_n = \frac{n}{2} [2a + (n-1)d]. \]
\[ 1050 = \frac{14}{2} [2(10) + 13d]. \]
\[ 1050 = 7 [20 + 13d]. \]
\[ 150 = 20 + 13d. \]
\[ 13d = 130. \]
\[ d = 10. \]
Now,
\[ a_{20} = a + (20-1)d = 10 + 19(10) = 200. \] Quick Tip: Use the sum formula to find the common difference before solving for any term.
Find the sum of the first 22 terms of an A.P. in which the common difference is 7 and the 22nd term is 149.
View Solution
We use the formula for the \( n \)th term of an arithmetic progression:
\[ a_n = a + (n - 1)d. \]
Given:
\[ a_{22} = 149, \quad d = 7, \quad n = 22. \]
Substituting the values:
\[ 149 = a + (22 - 1) \times 7. \]
\[ 149 = a + 21 \times 7. \]
\[ 149 = a + 147. \]
\[ a = 2. \]
Now, we calculate the sum of the first 22 terms:
\[ S_n = \frac{n}{2} [2a + (n-1)d]. \]
\[ S_{22} = \frac{22}{2} [2(2) + (22-1) \times 7]. \]
\[ = 11 [4 + 21 \times 7]. \]
\[ = 11 [4 + 147]. \]
\[ = 11 \times 151. \]
\[ = 1661. \] Quick Tip: For sum of an arithmetic sequence, use: \[ S_n = \frac{n}{2} [2a + (n-1)d]. \]
Each side of an equilateral triangle \( ABC \) is \( a \). Prove that the altitude of the triangle is \( \frac{\sqrt{3}}{2} a \).
View Solution
In an equilateral triangle, the altitude divides the triangle into two right-angled triangles.
Using Pythagoras’ theorem:
\[ h^2 + \left(\frac{a}{2}\right)^2 = a^2. \]
\[ h^2 = a^2 - \frac{a^2}{4} = \frac{3a^2}{4}. \]
\[ h = \frac{\sqrt{3}}{2} a. \] Quick Tip: Use Pythagoras’ theorem in an equilateral triangle by splitting it into two right triangles.
Find the discriminant of the quadratic equation \( 9x^2 - 6x + 1 = 0 \) and hence find the nature of the roots.
View Solution
The discriminant of a quadratic equation \( ax^2 + bx + c = 0 \) is given by:
\[ \Delta = b^2 - 4ac. \]
For \( 9x^2 - 6x + 1 = 0 \):
\[ \Delta = (-6)^2 - 4(9)(1) = 36 - 36 = 0. \]
Since \( \Delta = 0 \), the roots are real and equal.
Quick Tip: If \( \Delta > 0 \), roots are real and distinct; if \( \Delta = 0 \), roots are real and equal; if \( \Delta < 0 \), roots are imaginary.
For what values of \( k \) does the quadratic equation \( (k+1)x^2 - 2(k-1)x + 1 = 0 \) have equal roots?
View Solution
For equal roots, the discriminant must be zero:
\[ \Delta = b^2 - 4ac = 0. \]
\[ [ -2(k-1)]^2 - 4(k+1)(1) = 0. \]
\[ 4(k-1)^2 - 4(k+1) = 0. \]
\[ (k-1)^2 - (k+1) = 0. \]
Expanding:
\[ k^2 - 2k + 1 - k - 1 = 0. \]
\[ k^2 - 3k = 0. \]
\[ k(k-3) = 0. \]
\[ k = 0 or k = 3. \] Quick Tip: Set the discriminant to zero for conditions of equal roots.
If the 3rd and 9th terms of an A.P. are 4 and -8 respectively, which term of this A.P. is zero?
View Solution
Using the formula for the \( n \)th term:
\[ a_n = a + (n-1)d. \]
For 3rd term:
\[ a + 2d = 4. \]
For 9th term:
\[ a + 8d = -8. \]
Subtracting:
\[ ( a + 8d) - (a + 2d) = -8 - 4. \]
\[ 6d = -12. \]
\[ d = -2. \]
Substituting in \( a + 2d = 4 \):
\[ a + 2(-2) = 4. \]
\[ a - 4 = 4. \]
\[ a = 8. \]
Finding \( n \) where \( a_n = 0 \):
\[ 8 + (n-1)(-2) = 0. \]
\[ 8 - 2(n-1) = 0. \]
\[ 8 = 2(n-1). \]
\[ n-1 = 4. \]
\[ n = 5. \]
Thus, the 5th term is zero.
Quick Tip: Use simultaneous equations to find \( a \) and \( d \) in an arithmetic sequence.
For what value of \( k \), do the equations \( kx + y = 1 \) and \( (k+1)x + 2y = 3 \) have no solution?
View Solution
For a system of equations to have no solution, the lines must be parallel, which occurs when:
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}. \]
Comparing with \( ax + by = c \):
\[ \frac{k}{k+1} = \frac{1}{2} \neq \frac{1}{3}. \]
Cross multiplying:
\[ 2k = k+1. \]
\[ 2k - k = 1. \]
\[ k = 1. \]
Thus, for \( k = 1 \), the system has no solution.
Quick Tip: For parallel lines, the ratios of coefficients of \( x \) and \( y \) must be equal, but not the constant terms.
Find the value of \( 4\tan^2 45^\circ + \cos^2 30^\circ - \sin^2 60^\circ \).
View Solution
Using trigonometric values:
\[ \tan 45^\circ = 1, \quad \cos 30^\circ = \frac{\sqrt{3}}{2}, \quad \sin 60^\circ = \frac{\sqrt{3}}{2}. \]
\[ 4\tan^2 45^\circ = 4(1)^2 = 4. \]
\[ \cos^2 30^\circ = \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{3}{4}. \]
\[ \sin^2 60^\circ = \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{3}{4}. \]
\[ 4 + \frac{3}{4} - \frac{3}{4} = 4. \] Quick Tip: Use standard trigonometric values to simplify expressions.
Find the roots of the equation \( x + \frac{1}{x} = 3, \quad x \neq 0 \).
View Solution
Multiplying both sides by \( x \):
\[ x^2 + 1 = 3x. \]
\[ x^2 - 3x + 1 = 0. \]
Using the quadratic formula:
\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(1)}}{2(1)}. \]
\[ = \frac{3 \pm \sqrt{9 - 4}}{2}. \]
\[ = \frac{3 \pm \sqrt{5}}{2}. \]
Thus, the roots are:
\[ \frac{3+\sqrt{5}}{2}, \quad \frac{3-\sqrt{5}}{2}. \] Quick Tip: Convert equations into standard quadratic form before solving.
An isosceles triangle has \( AB = AC = 13 \) cm. If the length of the perpendicular from vertex \( A \) to \( BC \) is 5 cm, find the length of \( BC \).
View Solution
In an isosceles triangle, the perpendicular from the vertex bisects the base.
Using Pythagoras' theorem:
\[ AB^2 = AD^2 + BD^2. \]
\[ 13^2 = 5^2 + BD^2. \]
\[ 169 = 25 + BD^2. \]
\[ BD^2 = 144. \]
\[ BD = 12. \]
Since \( BC = 2BD \):
\[ BC = 24 cm. \] Quick Tip: In an isosceles triangle, the altitude bisects the base.
Find the value of \( x \) for which the distance between the points \( P(x, 4) \) and \( Q(9,10) \) is 10 units.
View Solution
Using distance formula:
\[ \sqrt{(x - 9)^2 + (4 - 10)^2} = 10. \]
\[ \sqrt{(x - 9)^2 + 36} = 10. \]
Squaring both sides:
\[ (x - 9)^2 + 36 = 100. \]
\[ (x - 9)^2 = 64. \]
\[ x - 9 = \pm 8. \]
\[ x = 17 or x = 1. \] Quick Tip: Use the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
In what ratio does the point \( (-1,6) \) divide the line segment joining the points \( (-3,10) \) and \( (6,-8) \)?
View Solution
Using the section formula:
\[ (x, y) = \left( \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}, \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2} \right). \]
Let the ratio be \( m:n \).
\[ (-1,6) = \left( \frac{6m + (-3n)}{m+n}, \frac{-8m + 10n}{m+n} \right). \]
Equating \( x \)-coordinates:
\[ \frac{6m - 3n}{m+n} = -1. \]
\[ 6m - 3n = -m - n. \]
\[ 6m + m = 3n - n. \]
\[ 7m = 2n. \]
\[ \frac{m}{n} = \frac{2}{7}. \]
Thus, the required ratio is \( 2:7 \).
Quick Tip: Use the section formula to divide a line segment in a given ratio.
A ladder 15 m long makes an angle of \( 60^\circ \) with the wall. Find the height of the point on the wall where the ladder touches the wall.
View Solution
Using trigonometry, the height of the point where the ladder touches the wall is given by:
\[ h = L \sin \theta. \]
\[ h = 15 \sin 60^\circ. \]
\[ = 15 \times \frac{\sqrt{3}}{2}. \]
\[ = \frac{15\sqrt{3}}{2}. \]
Approximating \( \sqrt{3} = 1.732 \):
\[ h = \frac{15 \times 1.732}{2} = \frac{25.98}{2} = 12.99 \approx 13 m. \] Quick Tip: For problems involving ladders leaning against walls, use trigonometric functions like sine and cosine.
The length of the minute hand of a clock is 15 cm. Find the area swept by it in 20 minutes.
View Solution
Angle swept in 60 minutes:
\[ 360^\circ. \]
Angle swept in 20 minutes:
\[ \frac{20}{60} \times 360 = 120^\circ. \]
Area swept:
\[ A = \frac{\theta}{360} \pi r^2. \]
\[ = \frac{120}{360} \pi (15)^2. \]
\[ = \frac{1}{3} \pi \times 225. \]
\[ = 75\pi. \]
Approximating \( \pi = 3.14 \):
\[ = 235.5 cm^2. \] Quick Tip: For circular motion, use \( A = \frac{\theta}{360} \pi r^2 \).
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is more than 9.
View Solution
Total possible outcomes when two dice are rolled:
\[ 6 \times 6 = 36. \]
Favorable outcomes for sum \( > 9 \):
\[ (4,6), (5,5), (5,6), (6,4), (6,5), (6,6). \]
Total favorable outcomes = 6.
Probability:
\[ P(E) = \frac{Favorable outcomes}{Total outcomes} = \frac{6}{36} = \frac{1}{6}. \] Quick Tip: List all possible outcomes and count favorable cases before calculating probability.
Draw the graph of the pair of linear equations \( 3x - 5y + 1 = 0 \) and \( 2x - y + 3 = 0 \) and solve them.
View Solution
To solve this system graphically, we find the coordinates where these two lines intersect.
Step 1: Expressing in Slope-Intercept Form
Rearrange both equations:
\[ y = \frac{3}{5}x + \frac{1}{5} \]
\[ y = 2x + 3 \]
Step 2: Finding Intercepts
For \( 3x - 5y + 1 = 0 \):
- When \( x = 0 \), \( y = -\frac{1}{5} \).
- When \( y = 0 \), \( x = -\frac{1}{3} \).
For \( 2x - y + 3 = 0 \):
- When \( x = 0 \), \( y = -3 \).
- When \( y = 0 \), \( x = \frac{3}{2} \).
Step 3: Plotting and Finding Intersection
Plot these points on a graph, and the intersection point gives the solution.
Quick Tip: For graphical solutions, convert equations to \( y = mx + c \) form and plot the intercepts.
The area of a rectangular field is 260 square meters. If its length becomes 5 meters less and breadth 2 meters more, it becomes a square field. Find the length and breadth of the rectangular field.
View Solution
Let the original length and breadth of the rectangular field be \( l \) and \( b \).
Given:
\[ l \times b = 260. \]
When modified:
\[ (l - 5) = (b + 2). \]
Thus,
\[ l - 5 = b + 2. \]
\[ l - b = 7. \]
Solving \( l \times b = 260 \) and \( l - b = 7 \):
Substituting \( l = b + 7 \) in the area equation:
\[ (b+7) \times b = 260. \]
\[ b^2 + 7b - 260 = 0. \]
Using the quadratic formula:
\[ b = \frac{-7 \pm \sqrt{49 + 1040}}{2} = \frac{-7 \pm 33}{2}. \]
\[ b = 13, \quad l = 20. \]
Thus, \( l = 20 \) meters, \( b = 13 \) meters.
Quick Tip: When a rectangle is modified into a square, set length equal to breadth plus/minus changes.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View Solution
Given two similar triangles \( \triangle ABC \sim \triangle PQR \), we need to prove:
\[ \frac{Area(\triangle ABC)}{Area(\triangle PQR)} = \frac{AB^2}{PQ^2} = \frac{BC^2}{QR^2} = \frac{AC^2}{PR^2}. \]
Proof:
For two similar triangles, their corresponding angles are equal, and their sides are proportional:
\[ \frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR} = k. \]
Area of a triangle:
\[ Area = \frac{1}{2} \times Base \times Height. \]
Since height is also proportional:
\[ h_1 = k h_2. \]
Thus, the ratio of the areas is:
\[ \frac{Area(\triangle ABC)}{Area(\triangle PQR)} = \frac{\frac{1}{2} AB \times h_1}{\frac{1}{2} PQ \times h_2}. \]
\[ = \frac{AB}{PQ} \times \frac{h_1}{h_2} = k \times k = k^2. \]
Hence proved.
Quick Tip: For similar triangles, all corresponding sides and heights maintain the same ratio.
Prove that:
\[ \frac{\sec^3 0}{\sec^2 0 -1} + \frac{\cosec^3 0}{\cosec^2 0 -1} = \sec 0 \cosec 0 ( \sec 0 + \cosec 0 ). \]
View Solution
Step 1: Express in terms of trigonometric identities
We know:
\[ \sec^2 \theta - 1 = \tan^2 \theta, \quad \cosec^2 \theta - 1 = \cot^2 \theta. \]
Rewriting each term:
\[ \frac{\sec^3 \theta}{\sec^2 \theta -1} = \frac{\sec^3 \theta}{\tan^2 \theta} = \sec \theta \cdot \frac{1}{\cos \theta}. \]
Similarly,
\[ \frac{\cosec^3 \theta}{\cosec^2 \theta -1} = \frac{\cosec^3 \theta}{\cot^2 \theta} = \cosec \theta \cdot \frac{1}{\sin \theta}. \]
Step 2: Adding both expressions
\[ \sec \theta \cdot \frac{1}{\cos \theta} + \cosec \theta \cdot \frac{1}{\sin \theta}. \]
\[ = \sec \theta \cosec \theta (\sec \theta + \cosec \theta). \]
Thus, the given equation is proved.
Quick Tip: Use fundamental trigonometric identities to simplify complex expressions step by step.
A 20 m deep well with a diameter of 7 m is dug, and the soil from digging is evenly spread out to form a platform of 22 m × 14 m. Find the height of the platform.
View Solution
The volume of soil removed from the well:
\[ V_{well} = \pi r^2 h. \]
\[ = \pi \times \left(\frac{7}{2}\right)^2 \times 20. \]
\[ = \pi \times \frac{49}{4} \times 20 = 245\pi. \]
The volume of the platform:
\[ V_{platform} = Base Area \times Height. \]
\[ = (22 \times 14) \times h. \]
\[ = 308h. \]
Since soil volume remains constant:
\[ 245\pi = 308h. \]
Approximating \( \pi = 3.14 \):
\[ 245 \times 3.14 = 769.3. \]
\[ h = \frac{769.3}{308} \approx 2.5 m. \] Quick Tip: Volume before and after digging remains the same, apply volume conservation.
The angle of elevation of the top of a building from the foot of a tower is \( 30^\circ \), and the angle of elevation of the top of the tower from the foot of the building is \( 60^\circ \). If the tower is 50 m high, find the height of the building.
View Solution
Let the height of the building be \( h \) meters and the distance between the building and the tower be \( x \) meters.
Using the right triangle formed by the tower:
\[ \tan 60^\circ = \frac{50}{x}. \]
\[ \sqrt{3} = \frac{50}{x}. \]
\[ x = \frac{50}{\sqrt{3}} = \frac{50\sqrt{3}}{3}. \]
Now, using the right triangle formed by the building:
\[ \tan 30^\circ = \frac{h}{x}. \]
\[ \frac{1}{\sqrt{3}} = \frac{h}{\frac{50\sqrt{3}}{3}}. \]
\[ h = \frac{50\sqrt{3}}{3} \times \frac{1}{\sqrt{3}}. \]
\[ h = \frac{50}{3} = 16.67 m. \]
Thus, the height of the building is approximately 16.67 meters.
Quick Tip: Use right-angle trigonometry for height and distance problems involving angles of elevation and depression.
Construct a triangle with sides 4 cm, 5 cm, and 6 cm and then construct another triangle similar to it whose sides are \( \frac{2}{3} \) of the corresponding sides of the first triangle.
View Solution
Step 1: Constructing the original triangle
1. Draw a base \( BC = 6 \) cm.
2. Using a compass, draw an arc of radius 4 cm from \( B \).
3. Draw another arc of radius 5 cm from \( C \), intersecting the first arc at \( A \).
4. Connect \( A \) to \( B \) and \( C \) to form \( \triangle ABC \).
Step 2: Constructing the similar triangle
1. Draw a ray \( BX \) making an acute angle with \( BC \).
2. Mark 3 equal divisions along \( BX \) (since the required ratio is \( 2:3 \)).
3. Connect the third point to \( C \).
4. Draw a line parallel to \( C_3C \) through the second division point, meeting \( BC \) at \( C' \).
5. Draw a line parallel to \( AC \) through \( C' \), meeting \( AB \) at \( A' \).
Step 3: Triangle Verification
The triangle \( \triangle A'B'C' \) is similar to \( \triangle ABC \) by Basic Proportionality Theorem (BPT).
Thus, the required triangle with sides \( \frac{2}{3} \) of the original is successfully constructed.
Quick Tip: Use the Basic Proportionality Theorem (BPT) to construct a similar triangle with a given scale factor.
Find the mode of the following distribution:
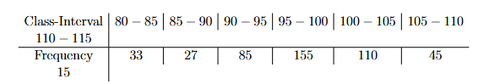
View Solution
The mode is the class with the highest frequency.
Here, the modal class is \( 95-100 \) with frequency 155.
Using the mode formula:
\[ Mode = L + \frac{(f_1 - f_0)}{2f_1 - f_0 - f_2} \times h. \]
\[ = 95 + \frac{(155 - 85)}{(2 \times 155 - 85 - 110)} \times 5. \]
\[ = 95 + \frac{70}{115} \times 5. \]
\[ = 95 + 3.04 \approx 98.04. \] Quick Tip: The mode is estimated using the modal class and interpolation formula.














































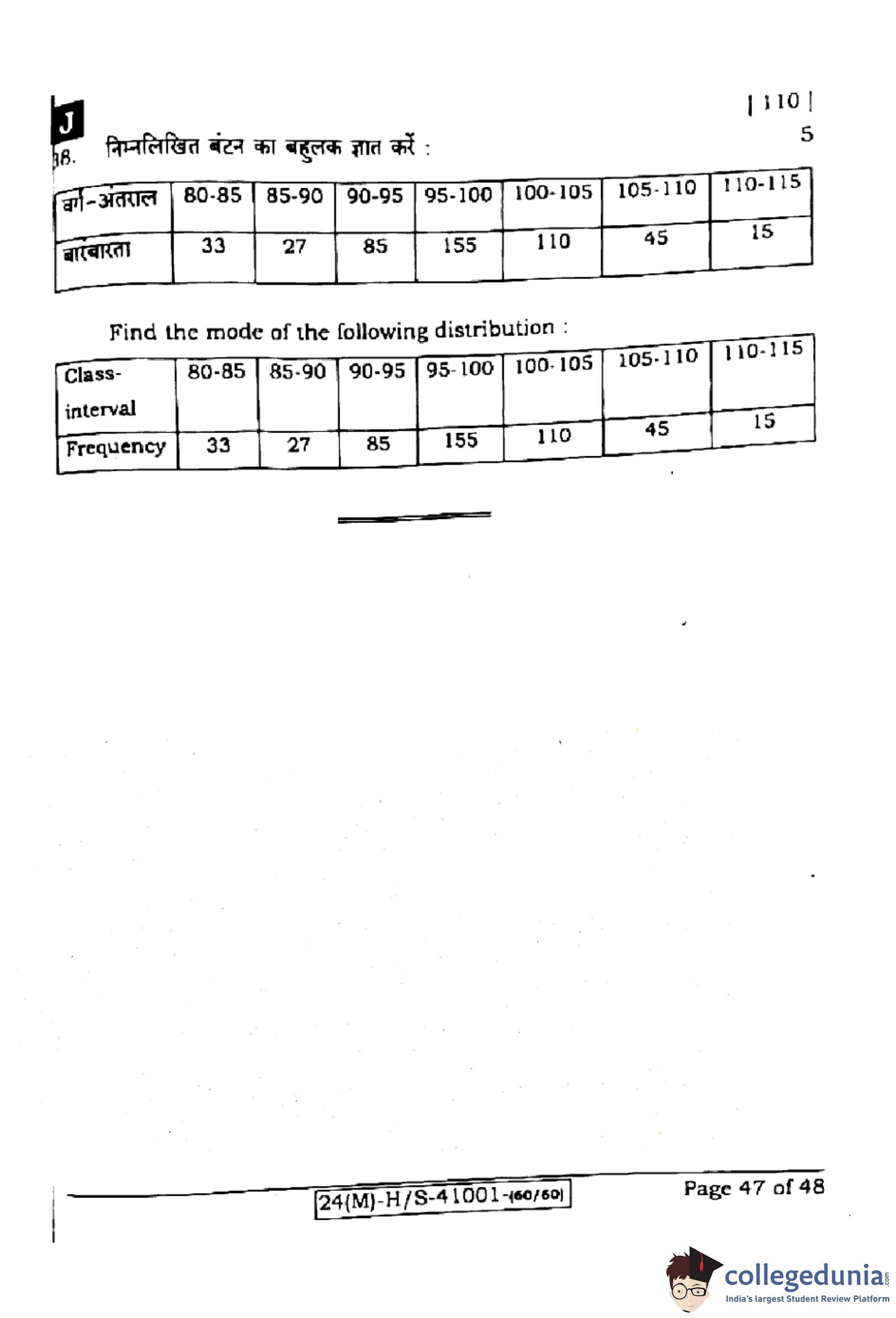



Comments