Content Curator
Energy of orbitals refers to the energy required to shift an electron from its orbital to infinity, or shift an electron from infinity to an orbital within the atom. It was Bohr who first laid down the model which describes the existence of orbitals/shells within atoms. Later, Arnold Sommerfeld argued the existence of elliptical orbitals, or subshells within shells as an extension to Bohr's model, which is how Azimuthal Quantum Numbers came into being. Three principles guide the calculation of energy levels of orbitals/filling up orbitals of an atom namely: Aufbau Principle, Pauli Exclusion and Hund's Rule of Maximum Multiplicity.
Key Takeaways: Energies of Orbitals, Quantum Numbers, Aufbau Principle, Pauli Exclusion Principle, Hund’s Rule of Maximum Multiplicity, Hydrogen
Energies of Orbitals
[Click Here for Sample Questions]
Energy of orbitals refers to the energy needed to take an electron present in that orbital to infinity or the energy released when that electron is shifted from infinity to that orbital. (The term “orbital” here refers to the region of space in which electrons populate). The energy of an orbital depends mainly on shell and subshells, or to put in technical terms, on principle quantum numbers and azimuthal quantum numbers respectively. (NOTE: Degenerate orbitals is the name given to orbitals belonging to the same subshell).
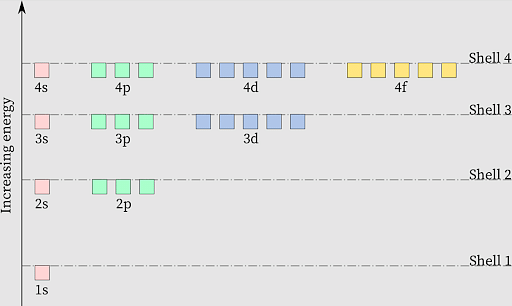
Energies of Orbitals
Principle Quantum Number (N)
[Click Here for Sample Questions]
It was Bohr who laid down the foundation of orbital chemistry as we know it today. He established that electron orbitals represent an energy level in terms of their distance from the nucleus of the atom. Accordingly, the orbitals were named as K,L,M,N or 1,2,3,4; in ascending order. These numbers are called Principal Quantum Numbers. The principal quantum number assigned to each electron in an atom describes the electron’s state. It is denoted by n and can take only positive integer values. For example, for the M orbital, n = 3.
Read More: What is Enthalpy
Azimuthal Quantum Number (L)
[Click Here for Sample Questions]
The azimuthal quantum number is an extended version of the Bohr model of the atom and was posited by Arnold Sommerfeld. He argues that other than the circular orbits established by Bohr, there are elliptical orbits as well meaning that every shell is constituted of multiple subshells.
The azimuthal quantum number is the quantum number for an atomic orbital that states the momentum of its orbital angular, along with explaining the orbital shape. It is the second set of quantum numbers which describes the unique quantum state of an electron. It helps in determining the ellipticity of the subshells and is denoted by “I”. It may also be referred to as orbital angular momentum quantum number/orbital quantum number/second quantum number.
Also Read:
Spectroscopic Symbols
In order to denote the value of ‘I’, the following spectroscopic symbols (way to specify atomic orbitals) are used:
| I | 0 | 1 | 2 | 3 | 4 |
| Spectroscopic Symbol | s | p | d | f | g |
Calculating the Energy Level of an Orbital
The electrons are filled into the orbitals of atoms in accordance with the following principles:
Aufbau Principle
[Click Here for Sample Questions]
This principle states that electrons occupy their respective energy orbitals in accordance with the increasing order of energies. This means that the first electrons target the lowest energy orbital and once the lowest region is occupied, they ascend into higher energy orbitals. (NOTE: This principle works when the atoms are in their ground state i.e. the physical state of the system of an atomic nucleus or atom having the least amount of energy among all the possible states.)
According to the Aufbau Principle, the energy of an orbital directly impacts the sum of the values of the principal quantum number and azimuthal quantum number. The order followed here is: 1s<2s<2p<3s<3p<4s…The diagram given below depicts increase in orbital energy and its impact on the filling of the orbital.
Read More: Atomic Radii
The (n+1) Rule
This rule establishes that when an atom is neutral and in an isolated state, its low energy is directly proportional to a lower value of an orbital. It is important to note that in case the orbitals have the same value, the lowest energy of the orbital (n+1) will be the one with the lower value of n.
| Relative Energy | Type of Orbitals | Values of n | Values of I | Values of n+I |
|---|---|---|---|---|
| Lowest Energy | 1s | 1 | 0 | 1+0=1 |
| Higher Energy than 1s Orbital | 2s | 2 | 0 | 2+0=2 |
| 3s Orbital (n=3) and a lower energy than 2p orbital (n=2) | 2p | 2 | 1 | 2+1=3 |
| 3s | 3 | 1 | 3+1=4 |
Pauli Exclusion Principle
[Click Here for Sample Questions]
According to this principle, the maximum orbital capacity of an electron must be 2. They must also be spinning in opposite directions. For instance, if one of the electrons has a clockwise revolution, the other must have an anticlockwise revolution.
Also Read:
| Discovery of Electron | Pauli Exclusion Principle |
| Hund’s Rule of Maximum Multiplicity | Limitations of Bohr’s Model |
Hund’s Rule of Maximum Multiplicity
[Click Here for Sample Questions]
As per this rule, the identical electrons in charge repel each other when coincided in the same orbit. In order to curb this repulsion, two electrons must be separated as far as possible from one another through the orchestrated placement of degenerate orbitals.
The stability of an atom is determined by the attraction between the electrons, along with a positively charged nucleus and repulsive force within the electrons. The reason behind different energies among the various subshells with the same shell is that there exists a mutual repulsion among the electrons in multi-electron atoms. Owing to the presence of electrons in the inner shell, the electrons of the outer shell are unable to experience a full-positive charge of the nucleus. This effect goes by the name ‘shielding effect’.
Read More: Hydrogen Spectrum
Energy of Orbital in a Single-Electron Atom (Hydrogen)
[Click Here for Sample Questions]
- The principles that were discussed above do not apply to the case of hydrogen, which is a single electron atom.
- In hydrogen, the energy of orbitals depends only on the principle quantum number. Thus, the 2s and 2p orbitals in a hydrogen atom have the same energy.
- It is important to note that the 1s orbital in a hydrogen atom corresponds to the most stable condition and is referred to as the ‘ground state’. However, any other orbital afterwards has a higher energy than the one contained in 1s and are called the excited state.
Hydrogen Atom
Points to Remember
- Energy of orbitals refers to the energy required to shift an electron from an orbital to infinity and vice-versa.
- Orbital refers to the region within an atom occupied by electrons.
- Bohr established the principle quantum number, while Arnold Sommerfeld posited the existence of elliptical orbits.
- Principle quantum number and azimuthal quantum number determine the energy of shells and subshells.
- The energy of orbitals is calculated in accordance with the Aufbau Principle, Pauli Exclusion and Hund’s Rule of Maximum Multiplicity.
Read More: Properties Of Matter
Sample Questions
Ques 1: What is the principle of quantum number? (2 marks)
Ans. The principal quantum number assigned to each electron in an atom describes the state of the electron. These quantum numbers are K,L,M,N or 1,2,3,4. They are denoted by n and can take up the value of only positive rational integers. These quantum numbers are associated with the energy states of the atoms. These numbers were created for use in the semiclassical Bohr's model of atoms.
Ques 2. What did Arnold Sommerfeld posit, in relation to Bohr’s model? (2 marks)
Ans. Arnold Sommerfeld argued that each shell in an atom is composed of subshells. He posited the existence of elliptical orbits within orbits and gave Azimuthal Quantum Numbers, denoted by I. Azimuthal Quantum Numbers determine the orbital angular momentum for an atomic orbital and are denoted by I. They also define the shape of the orbital.
Ques 3 Which is the lowest possible energy level in an electron? Which is the highest? (2 marks)
Ans. Ground state is the lowest possible energy level in an electron. In this state, the total energy of the electrons cannot be lowered by transferring electrons to different orbitals. It is the lowest energy state possible. Excited state is the highest possible energy level. It is any other state higher than the ground state.
Ques 4. What do you mean by an electron shell? (2 marks)
Ans. In an atom, the electron shell is the region surrounding the atomic nucleus. The term ‘electron shell’ is derived by the Bohr model according to which electron groups move around the nucleus at a particular distance from the nucleus. The term comes from Bohr's model of the atom, in which electrons were believed to orbit around the nucleus in certain distances.
Ques 5. On what factor does an atom’s energy level depend on? (1 mark)
Ans. An atom’s energy depends on the number of orbitals present within it. It is determined by the principal quantum number and azimuthal quantum number. The lower the value of (n+1) for an orbital, the lower is its energy.
Ques 6. Describe the Aufbau Principle. (2 marks)
Ans. This principle states that electrons occupy their respective energy orbitals in accordance with the increasing order of energies. This means that the first electrons target the lowest energy orbital and once the lowest region is occupied, they ascend into higher energy orbitals. The Aufbau principle works when the atoms are in their ground state i.e. the physical state of the system of an atomic nucleus or atom having the least amount of energy among all the possible states.
Ques 7. What is the (n+1) rule? (2 marks)
Ans. This rule establishes that when an atom is neutral and in an isolated state, its low energy is directly proportional to a lower value of an orbital. It is important to note that in case the orbitals have the same value, the lowest energy of the orbital (n+1) will be the one with the lower value of n.
Ques 8. How is the energy of orbitals different in the case of hydrogen atoms, which is a single-electron atom? (2 marks)
Ans. In hydrogen, the energy of orbitals depends only on the principle quantum number. Thus, the 2s and 2p orbitals in a hydrogen atom have the same energy. It is important to note that the 1s orbital in a hydrogen atom corresponds to the most stable condition and is referred to as the ‘ground state’. However, any other orbital afterwards has a higher energy than the one contained in 1s and is called the excited state.
Also Read:
Comments