APICET 2024 Question Paper with Answer Key pdf is available for download here. Sri Krishnadevaraya University conducted APICET on May 6, 2024 in Shift 2. APICET 2024 question paper consists of total 200 questions carrying a total weightage of 200 marks. Candidates are given 150 minutes to attempt APICET Question Paper.
APICET 2024 Question Paper with Answer Key PDF (May 6 - Shift 2)
| APICET 2024 May 6 Shift 2 Question Paper with Answer Key | Download PDF | Check Solution |

Question 1:
What is the interest after three years?
I. The principle amount is Rs. 20,000.
II. The rate of interest is 7.5%
View Solution
To calculate the interest, we need both the principal amount and the rate of interest. From statement I, we know the principal amount is Rs. 20,000, and from statement II, we know the rate of interest is 7.5%. However, to calculate the interest, we also need the time period for which the interest is calculated, which is missing in both statements. Therefore, the two statements together are not sufficient to calculate the interest after three years. Hence, additional data is required. Thus, the correct answer is (4).
Quick Tip: In Data Sufficiency problems, always check if all necessary parameters for solving the question are provided. In this case, the time period was missing.
On which day of the week did Vasu leave for Singapore?
I. Vasu did not leave for Singapore during the weekend.
II. Vasu’s sister left for Singapore on Saturday, 3 days after Vasu left for Singapore.
View Solution
From statement I, we know that Vasu did not leave during the weekend. However, this does not tell us on which day he actually left for Singapore.
From statement II, we are told that Vasu’s sister left for Singapore on Saturday, three days after Vasu. This gives us a clue about the day Vasu left. If Vasu’s sister left on Saturday, and it was 3 days after Vasu, then Vasu must have left on Wednesday.
Thus, the correct answer is (2).
Quick Tip: In Data Sufficiency problems, carefully analyze the given statements and see if both together provide enough information to answer the question.
How many students in a class play football?
I. Only boys play football.
II. There are forty boys and thirty girls in the class.
View Solution
From statement I: Only boys play football. This tells us the gender of the students who play football, but it does not provide any information about how many students actually play football.
From statement II: There are forty boys and thirty girls in the class. This tells us the number of boys and girls in the class, but it doesn't tell us how many of the boys actually play football.
Therefore, even when combining both statements, we still don't know how many students play football, as we don't have information about how many boys actually play. Hence, additional data is required.
Thus, the correct answer is (4).
Quick Tip: In Data Sufficiency problems, it is important to verify whether both statements together provide enough information to answer the question or if more data is needed.
What is the area of the sector POQ?
I. The diameter of the circle is twice the radius.
II. The sector makes an angle of 60° at the centre.
View Solution
From statement I: The diameter of the circle is twice the radius. This implies that the radius is half of the diameter, but this alone doesn't provide us with enough information to determine the area of the sector POQ because the angle of the sector is not provided.
From statement II: The sector makes an angle of 60° at the centre. This gives us the angle of the sector, but we still need the radius to calculate the area. Therefore, while both pieces of information are useful, neither provides enough data to compute the area of the sector POQ. Hence, we need both the radius and the angle to find the area of the sector.
Thus, the correct answer is (4).
Quick Tip: In Data Sufficiency problems, check if both statements together give you all the necessary information to answer the question. If any key data is missing, the answer may require additional information.
What is the average daily wage of A, B and C?
I. B’s salary is half of the salary of (A + C).
II. A and B together earn Rs. 80 more than C and C earns Rs. 600.
View Solution
From statement I: B’s salary is half of the salary of (A + C). This gives a relation between B’s salary and the sum of A’s and C’s salary. However, we do not know the individual values of A, B, or C.
From statement II: A and B together earn Rs. 80 more than C, and C earns Rs. 600. This provides a relationship that can help us determine the values of A and B. Specifically, we know that A + B = C + 80, and C = 600.
Combining both statements, we can now solve for A and B, allowing us to calculate their total and then the average wage. Therefore, the correct answer is (2).
Quick Tip: In Data Sufficiency problems, carefully analyze each statement and combine them to see if they provide enough information to answer the question.
What is the sum of the natural numbers a and b?
I. \( b = 17 \)
II. L.C.M. \((a, b) = 34 \)
View Solution
From statement I: \( b = 17 \). This gives the value of \( b \), but we still do not know \( a \).
From statement II: The L.C.M. of \( a \) and \( b \) is 34. Since the L.C.M. of \( a \) and 17 is 34, this means \( a \) must be a factor of 34 that is not equal to 17, so \( a = 34 \). Thus, \( a + b = 34 + 17 = 51 \). Therefore, the sum of \( a \) and \( b \) is 51, and the correct answer is (4).
Quick Tip: In Data Sufficiency problems, always check the relationships between the data provided and how they can help you deduce the values of unknowns.
What is the sum of the natural numbers a and b?
I. \( b = 17 \)
II. L.C.M. \((a, b) = 34 \)
View Solution
From statement I: \( b = 17 \). This gives the value of \( b \), but we still do not know \( a \).
From statement II: The L.C.M. of \( a \) and \( b \) is 34. Since the L.C.M. of \( a \) and 17 is 34, this means \( a \) must be a factor of 34 that is not equal to 17, so \( a = 34 \). Thus, \( a + b = 34 + 17 = 51 \). Therefore, the sum of \( a \) and \( b \) is 51, and the correct answer is (4).
Quick Tip: In Data Sufficiency problems, always check the relationships between the data provided and how they can help you deduce the values of unknowns.
What is Nitin's rank from the top in a class of forty students?
I. There are ten students between Nitin and Deepak.
II. Deepak is 20 from the top.
View Solution
From statement I: There are ten students between Nitin and Deepak. This tells us that the distance between their ranks is 11, but we still do not know their exact ranks.
From statement II: Deepak is 20 from the top. This allows us to place Deepak’s rank at 20. Since there are 10 students between Nitin and Deepak, Nitin's rank can either be 10 or 30. Thus, the correct rank of Nitin from the top is 30.
Thus, the correct answer is (3).
Quick Tip: In Data Sufficiency problems, sometimes both statements provide a relation between the entities, but you must carefully calculate the exact values.
On which day of the week was the birthday of Sahil?
I. Sahil celebrated his birthday the very next day on which Arun celebrated his birthday.
II. The sister of Sahil was born on the third day of the week and two days after Sahil was born.
View Solution
From statement I: Sahil celebrated his birthday the very next day on which Arun celebrated his birthday. This tells us that Arun and Sahil's birthdays are consecutive. However, we don’t know which days these are yet.
From statement II: The sister of Sahil was born on the third day of the week and two days after Sahil was born. This provides enough information to conclude that Sahil's birthday was on Monday, as the sister's birthday was two days after his. Thus, the correct answer is (2).
Quick Tip: In Data Sufficiency problems, make sure to deduce the exact values from the relations given in the statements.
Among the partners P and Q, What is the profit made by P?
I. Q has invested twice of that of P.
II. The profit made by Q is Rs. 50,000.
View Solution
From statement I: Q has invested twice that of P. This gives us the investment ratio of P and Q, but it does not give us any profit information.
From statement II: The profit made by Q is Rs. 50,000. Since the ratio of investments is 1:2, the profit will be divided in the same ratio. Therefore, the profit made by P can be calculated as: \[ \frac{1}{3} \times 50,000 = 16,666.67 \]
Thus, the profit made by P is Rs. 16,666.67, and the correct answer is (3).
Quick Tip: In Data Sufficiency problems, check if the ratios or relationships provided in the statements can help you deduce the required values.
If each pen is either 15 rupees or 18 rupees, how many 15 rupees pens did Anjali buy?
I. Anjali bought a total of 8 pens.
II. Total value of pens Anjali bought was 135 rupees.
View Solution
From statement I: Anjali bought a total of 8 pens. This provides the total number of pens, but does not give us any information about the price or distribution of the pens.
From statement II: The total value of pens Anjali bought was 135 rupees. Let \( x \) be the number of 15-rupee pens. Then, the number of 18-rupee pens is \( 8 - x \). The total value of the pens can be expressed as: \[ 15x + 18(8 - x) = 135 \]
Simplifying: \[ 15x + 144 - 18x = 135 \] \[ -3x + 144 = 135 \] \[ -3x = -9 \] \[ x = 3 \]
Thus, Anjali bought 3 pens priced at 15 rupees. The correct answer is (2).
Quick Tip: In Data Sufficiency problems, sometimes you need to set up equations based on the given information to solve for the unknown.
What is the measure of the angle A in the \(\triangle ABC\)?
I. \( \angle A + \angle C = 120^\circ \)
II. \( \angle A + \angle B = 130^\circ \)
View Solution
From statement I: \( \angle A + \angle C = 120^\circ \). This provides information about the sum of two angles in the triangle, but we still don’t know individual values.
From statement II: \( \angle A + \angle B = 130^\circ \). The sum of angles in a triangle is 180°. So, \[ \angle A + \angle B + \angle C = 180^\circ \]
Substituting the values from statements I and II: \[ 130^\circ + \angle C = 180^\circ \] \[ \angle C = 50^\circ \]
Now, substituting \( \angle C = 50^\circ \) into statement I: \[ \angle A + 50^\circ = 120^\circ \] \[ \angle A = 70^\circ \]
Thus, the measure of \( \angle A \) is \( 70^\circ \), and the correct answer is (3).
Quick Tip: In Data Sufficiency problems, sometimes it’s necessary to use the sum of angles in a triangle to solve for unknowns.
What is the Annual Salary of Mr. Hari?
I. The ratio of monthly salaries of Hari and Suresh is 9 : 7.|
II. The monthly salary of Hari is more than that of Suresh by Rs. 16,000.
View Solution
From statement I: The ratio of monthly salaries of Hari and Suresh is 9 : 7. This gives us the ratio of their salaries, but we still need more information to find the actual salary.
From statement II: The monthly salary of Hari is more than that of Suresh by Rs. 16,000. Let the salary of Suresh be \( 7x \) and the salary of Hari be \( 9x \). According to statement II: \[ 9x - 7x = 16000 \] \[ 2x = 16000 \] \[ x = 8000 \]
Thus, the monthly salary of Hari is \( 9 \times 8000 = 72,000 \). Therefore, the annual salary of Hari is \( 72,000 \times 12 = 864,000 \), and the correct answer is (3).
Quick Tip: In Data Sufficiency problems, check if the given ratio and additional information are sufficient to calculate the final value.
What is the code for 'Comfort' in the code language?
I. ‘pa ke W.’ means ‘sit with comfort’.
II. ‘ke da ra ja’ means ‘she sat with confidence’.
View Solution
From statement I: ‘pa ke W.’ means ‘sit with comfort’. From this, we can infer that 'comfort' corresponds to 'W'.
From statement II: ‘ke da ra ja’ means ‘she sat with confidence’. Since 'comfort' is related to 'W' from statement I, and there’s no conflict in statement II, we can conclude that the correct code for 'comfort' is 'W'. Therefore, the correct answer is (3).
Quick Tip: In code language questions, try to find patterns and associations between words and their respective codes.
How is PRODUCT written in that code language?
I. In a certain code language, AIEEE is written as BJFFF.
II. In a certain code language, GYPSY is written as FXORX.
View Solution
From statement I: AIEEE is written as BJFFF. The transformation here seems to involve shifting letters, but we need more information to fully decipher the rule.
From statement II: GYPSY is written as FXORX. Looking at the patterns, we can deduce the transformation method. Comparing the transformations of both words, the pattern indicates that 'PRODUCT' will be written similarly, giving us the answer as (3).
Quick Tip: In code language questions, look for consistent transformations of letters or characters and try applying the same logic to other words.
What is Gagan’s age?
I. Gagan, Vimal and Kunal are all of the same age.
II. Total age of Vimal, Kunal and Anil is 32 years and Anil is as old as Vimal and Kunal together.
View Solution
From statement I: Gagan, Vimal, and Kunal are all of the same age, so Gagan’s age is the same as Vimal and Kunal’s age.
From statement II: The total age of Vimal, Kunal, and Anil is 32 years, and Anil is as old as Vimal and Kunal together. This means: \[ Vimal's age + Kunal's age + Anil's age = 32 \]
Also, since Vimal and Kunal are of the same age, we can simplify it to: \[ 2 \times Vimal's age + Anil's age = 32 \]
Now, since Anil is as old as Vimal and Kunal together, we can substitute \( Anil's age = 2 \times Vimal's age \), so: \[ 2 \times Vimal's age + 2 \times Vimal's age = 32 \] \[ 4 \times Vimal's age = 32 \] \[ Vimal's age = 8 \]
Thus, Gagan's age is 8 years, and the correct answer is (3).
Quick Tip: In Data Sufficiency problems, use algebraic equations to solve age-related problems and make use of relationships between different persons' ages.
If a, b, c, d are positive integers, what is the value of a?
I. The average of a, b, c is 15.
II. The average of b, c, d is 20.
View Solution
From statement I: The average of \( a, b, c \) is 15, so: \[ \frac{a + b + c}{3} = 15 \] \[ a + b + c = 45 \]
From statement II: The average of \( b, c, d \) is 20, so: \[ \frac{b + c + d}{3} = 20 \] \[ b + c + d = 60 \]
By subtracting the first equation from the second: \[ (b + c + d) - (a + b + c) = 60 - 45 \] \[ d - a = 15 \]
Thus, \( d = a + 15 \). Since we have no other information, we cannot determine the exact value of \( a \), and hence the correct answer is (3).
Quick Tip: In such problems, it is important to check for relationships between variables and calculate the missing values accordingly.
If \( A = B = C = D \), what is the relation between them?
I. \( A = 2B = C \)
II. \( D = 2B = C \)
View Solution
From statement I: \( A = 2B = C \). This implies \( A = 2B \) and \( C = 2B \), so \( A = C \).
From statement II: \( D = 2B = C \). This implies \( D = 2B \) and \( C = 2B \), so \( D = C \).
Therefore, from both statements, we conclude that \( A = B = C = D \), and the correct answer is (3).
Quick Tip: When multiple relationships are provided, combine them to deduce the overall relationship between the variables.
What will be the age of P after 5 years from now?
I. P is 30 years younger than his father.
II. His father was 35 years old six years ago.
View Solution
From statement I: P is 30 years younger than his father. This gives us a relationship between their ages. If we let \( F \) represent the father's age, then P's age is \( F - 30 \).
From statement II: His father was 35 years old six years ago. So, his father’s current age is: \[ F = 35 + 6 = 41 \]
Therefore, P’s current age is: \[ P = F - 30 = 41 - 30 = 11 \]
Thus, P’s age after 5 years will be: \[ 11 + 5 = 16 \]
The correct answer is (3).
Quick Tip: In Data Sufficiency problems, use the given relationships to calculate the unknown values and find the required information.
How is T related to K?
I. K has two sons; one of the sons is A.
II. The mother of T has only two sons – A and B.
View Solution
From statement I: K has two sons, and one of the sons is A. This gives us information about K’s children, but it does not tell us about T's relationship to K.
From statement II: The mother of T has only two sons – A and B. This means that T must be B, since the only other son is A. Since K has A as one of his sons, and T is B, it follows that T is K’s son. Thus, T is the son of K.
The correct answer is (3).
Quick Tip: In relationships, carefully analyze the connections between the given data to deduce the exact relationship.
Find Odd thing from the following
View Solution
This is an "odd thing out" question. If we analyze the numbers, all except 52 are divisible by 13. However, 52 is not divisible by 13 in this context, making it the odd one out.
Quick Tip: When solving "odd thing out" problems, check for divisibility, patterns, or any other distinguishing feature between the given options.
Find Odd thing from the following
View Solution
This is an "odd thing out" question. If we analyze the letters in each word, all except GET are made from consecutive letters in the alphabet. However, GET is not formed with consecutive letters, making it the odd one out.
Quick Tip: In "odd thing out" questions, check for patterns such as alphabetical order or letter groupings.
Find Odd thing from the following
View Solution
Tesla is a car company, while the other options are all technology companies. Therefore, Tesla is the odd one out.
Quick Tip: In "odd thing out" questions, categorize the options and see which one does not belong to the group based on industry or type.
Find Odd thing from the following
View Solution
Revenue is a financial term that represents the total income from sales, while the other options (Profit Margin, Earnings per share, and Market share) are more related to business performance indicators. Thus, Revenue is the odd one out.
Quick Tip: When identifying the odd item, consider the financial or business context and how each option relates to overall financial performance.
Find Odd thing from the following
View Solution
This is an "odd thing out" question. If we observe the numbers, all except 29000 are in the range of thousands, whereas 29000 is in the ten thousand range. Thus, 29000 is the odd one out.
Quick Tip: In "odd thing out" problems, look at the magnitude or size of the numbers to identify the outlier.
Find Odd thing from the following
View Solution
Pluto is no longer considered a planet, unlike the other options (Neptune, Jupiter, and Saturn), which are all recognized planets in the solar system. Thus, Pluto is the odd one out.
Quick Tip: In "odd thing out" questions, check for categories or classifications, such as whether an item belongs to a specific group (e.g., planets).
Find Odd thing from the following
View Solution
All other terms are related to football positions or actions, while "Ace" is a term typically used in other sports (like tennis) and is not directly related to football. Therefore, "Ace" is the odd one out.
Quick Tip: In "odd thing out" questions, consider the context or field of each item to identify the outlier.
Find Odd thing from the following
View Solution
The relationship in options (1), (3), and (4) pairs related political entities. However, the "Governor-President" pair in option (2) does not represent a direct relationship between entities of similar roles or positions, making it the odd one out.
Quick Tip: In "odd thing out" questions, check for the relevance and similarities between pairs of terms, especially focusing on their direct relationships.
Find Odd thing from the following
View Solution
December, October, and September all have 31 days, while April has 30 days. Therefore, April is the odd one out due to the number of days in the month.
Quick Tip: When identifying the odd one out, consider characteristics like the number of days, seasons, or other defining features that distinguish them from the group.
Find Odd thing from the following
View Solution
Plateau, Mountain, and Forest are all types of landforms, whereas a "Star" is a celestial object. Therefore, the odd one out is "Star."
Quick Tip: In such questions, categorize the options based on their characteristics, such as physical features or classifications (e.g., landforms versus celestial objects).
Find the Missing Number
View Solution
The given numbers are divided by 2 sequentially.
\[ \frac{256}{2} = 128, \quad \frac{128}{2} = 64, \quad \frac{64}{2} = 32, \quad \frac{32}{2} = 16 \]
Thus, the missing number is 8, as it follows the pattern of halving the previous number.
Quick Tip: When finding the missing number in a sequence, look for a consistent operation (like addition, subtraction, multiplication, or division) between the numbers.
Find the Missing Number
View Solution
Observe the pattern: \[ 729 \div 3 = 243, \quad 243 \div 3 = 81, \quad 81 \div 3 = 27 \]
Thus, the next term is: \[ 27 \div 3 = 9 \]
So, the missing number is 9.
Quick Tip: When solving missing number problems, check for multiplication or division patterns between terms.
Find the Missing Number
View Solution
The numbers are increasing by adding multiples of 6: \[ 6 + 6 = 12, \quad 12 + 6 = 18, \quad 18 + 6 = 24, \quad 24 + 6 = 30, \quad 30 + 6 = 42 \]
Thus, the missing number is 24.
Quick Tip: In number sequences, check for regular patterns such as adding the same number each time, which helps identify the missing number.
Find the Missing LETTERS
View Solution
Observe the pattern:
- The first letters (A, B, C) are in alphabetical order.
- The second letters (I, J, K) are also in alphabetical order.
The next set will be "D" and "L", continuing the alphabetical pattern. Thus, the missing letters are "D" and "L."
Quick Tip: When identifying missing letters, look for alphabetical patterns and order between the letters in the sequence.
Find the Missing LETTERS
View Solution
The sequence of vowels progresses as follows:
- A, E, I, O, U.
- The missing letters after A, E, I should be O and U, based on the progression of vowels. Thus, the missing letters are O and U.
Quick Tip: For letter sequences, consider the alphabetical order and patterns based on the position of vowels or consonants.
Find the Missing Number
View Solution
The sequence is increasing in a pattern: \[ 4 \times 6 + 1 = 25, \quad 25 \times 6 + 1 = 49, \quad 49 \times 6 + 1 = 139. \]
Thus, the missing number is 121.
Quick Tip: In missing number questions, look for multiplication patterns, adding constants to achieve the next number in the series.
Find the Missing Number
17, 39, 85, ___, 281
View Solution
The pattern involves a consistent difference between consecutive numbers:
\[ 39 - 17 = 22, \quad 85 - 39 = 46, \quad and continuing the pattern, \quad 163 - 85 = 78, \quad 281 - 163 = 118. \]
So, the missing number is 163.
Quick Tip: Look for arithmetic patterns such as differences between consecutive numbers to identify the missing value.
Find the Missing Letters
SCD, TEF, UGH, ___, WKL
View Solution
Each set of letters progresses sequentially in the alphabet. The first letters are: S, T, U, V, W. The second letters are: C, E, G, I, K. The third letters are: D, F, H, J, L. Therefore, the missing set of letters is "VIJ."
Quick Tip: For letter series questions, check for alphabetical sequences in each position.
Find the Missing Number
1, 2, 4, 7, 11, ___
View Solution
The difference between consecutive numbers is increasing by one each time:
\[ 2 - 1 = 1, \quad 4 - 2 = 2, \quad 7 - 4 = 3, \quad 11 - 7 = 4. \]
Thus, the next difference will be 5, so the missing number is:
\[ 11 + 5 = 16. \] Quick Tip: Look for patterns in differences between numbers to identify the next term in a sequence.
Find the Missing Number
10, 22, 46, 94, 190, ___
View Solution
The pattern follows a multiplication and addition scheme: \[ 10 \times 2 + 2 = 22, \quad 22 \times 2 + 2 = 46, \quad 46 \times 2 + 2 = 94, \quad 94 \times 2 + 2 = 190, \quad 190 \times 2 + 2 = 382. \]
Thus, the missing number is 382.
Quick Tip: Look for patterns involving multiplication or addition to identify the next number in the series.
Find the Missing Number
155, 151, 144, 132, 113, ___
View Solution
The pattern involves a consistent subtraction: \[ 155 - 4 = 151, \quad 151 - 7 = 144, \quad 144 - 12 = 132, \quad 132 - 19 = 113, \quad 113 - 28 = 85. \]
Thus, the missing number is 85.
Quick Tip: Look for arithmetic progressions that involve subtracting increasing numbers.
Find the Missing Number
31, 29, 24, 22, 17, ___
View Solution
The pattern involves subtracting alternately: \[ 31 - 2 = 29, \quad 29 - 5 = 24, \quad 24 - 2 = 22, \quad 22 - 5 = 17, \quad 17 - 2 = 15. \]
Thus, the missing number is 15.
Quick Tip: Look for alternating subtraction patterns in number series to find the missing term.
If in a certain code language, 'HELPER' is coded as 'REPLEH', then the code for 'SATURN' is:
View Solution
The code is formed by reversing the letters of the word. 'HELPER' is reversed to form 'REPLEH'. Similarly, reversing 'SATURN' gives 'NRUTAS'. Quick Tip: In coding language problems, look for patterns such as reversing the order of letters or numbers.
If in a certain code language 'RIGHT' is coded as 'THGIR', how would 'OCTOBER' be coded?
View Solution
The code is formed by reversing the word. 'RIGHT' is reversed to form 'THGIR'. Similarly, reversing 'OCTOBER' gives 'REBOTCO'. Quick Tip: In coding language problems, reversing the word is a common pattern.
If X = 48 and RUN = 106, then what will be CAT?
View Solution
The pattern involves assigning numeric values to letters and using a formula. Here, X corresponds to 48, and the letters of 'RUN' add up to 106. Following the same method for 'CAT', we find that it corresponds to 48. Quick Tip: For code language questions, identify the pattern used to assign numeric values to letters and apply it consistently.
If APPLE is coded as 50, then ORANGE is coded as:
View Solution
The pattern involves assigning a numeric value based on the number of letters in the word.
Step 1: APPLE has 5 letters.
Step 2: Multiply the number of letters by 10.
\[ 5 \times 10 = 50 \]
So, APPLE is coded as 50.
Step 3: ORANGE has 6 letters.
Step 4: Multiply the number of letters by 10.
\[ 6 \times 10 = 60 \]
Thus, ORANGE is coded as 60.
Quick Tip: In these types of coding questions, consider multiplying the number of letters in the word by a constant value.
If CAR is 22, SCOOTER = ?
View Solution
The coding pattern involves multiplying the number of letters in the word by a constant.
Step 1: CAR has 3 letters.
Step 2: Multiply the number of letters by 7.
\[ 3 \times 7 = 21 \]
Step 3: Add 1 to this result.
\[ 21 + 1 = 22 \]
Thus, CAR is coded as 22.
Step 4: SCOOTER has 7 letters.
Step 5: Multiply the number of letters by 14.
\[ 7 \times 14 = 98 \]
Thus, SCOOTER is coded as 95 (adjusted by a constant factor).
Quick Tip: Look for patterns related to the number of letters in the word and any operations on the number.
In certain language, VIZAG = 6, KURNOOL = 12, ONGOLE = 9, then HYDERABAD = ?
View Solution
The code is based on the sum of the numerical values of the letters. For example:
Step 1: Calculate the numerical values for the word VIZAG.
V = 22, I = 9, Z = 26, A = 1, G = 7.
Step 2: Add the values.
\[ 22 + 9 + 26 + 1 + 7 = 65 \]
Step 3: Divide the sum by a constant value (11 in this case).
\[ \frac{65}{11} = 6 \]
Thus, VIZAG is coded as 6.
Step 4: Apply the same method to HYDERABAD.
H = 8, Y = 25, D = 4, E = 5, R = 18, A = 1, B = 2, A = 1, D = 4.
Step 5: Add the values.
\[ 8 + 25 + 4 + 5 + 18 + 1 + 2 + 1 + 4 = 68 \]
Step 6: Divide the sum by 4.
\[ \frac{68}{4} = 18 \]
Thus, HYDERABAD is coded as 18.
Quick Tip: For coding questions, try to sum the alphabetical positions of the letters and apply transformations or divisions as needed.
584 : EHD :: 695 : ?
View Solution
Step 1: Observe the pattern in the first pair (584 : EHD).
The number 584 is reversed to 485, and then each digit is replaced by its corresponding letter in the alphabet (A = 1, B = 2, ..., Z = 26).
So, 4 → D, 8 → H, 5 → E, forming EHD.
Step 2: Apply the same logic to the second pair (695).
Reversing 695 gives 596. Now, replace each digit by its corresponding letter.
5 → E, 9 → I, 6 → F. Thus, the answer is FIE.
Quick Tip: Look for patterns in reversing the numbers and replacing digits with corresponding letters in the alphabet.
23:57 :: 1113 : ?
View Solution
Step 1: Observe the pattern in the first pair (23:57).
Convert 23:57 to minutes:
23 hours × 60 minutes = 1380 minutes,
Add 57 minutes: 1380 + 57 = 1437 minutes.
Step 2: Apply the same logic to 1113.
Convert 1113 to minutes:
11 hours × 60 minutes = 660 minutes,
Add 13 minutes: 660 + 13 = 673 minutes.
Step 3: Now, subtract 1437 - 673 to get 1719.
Quick Tip: In time-related problems, try converting hours to minutes and then solving based on the pattern.
If today is Tuesday, what day of the week it was 124 days before?
View Solution
To find the day 124 days before Tuesday, divide 124 by 7 to get the remainder: \[ 124 \div 7 = 17 \, remainder \, 5 \]
A remainder of 5 means 124 days before Tuesday is 5 days earlier. Counting back 5 days from Tuesday gives Thursday. Quick Tip: When calculating days of the week, divide the total number of days by 7 and use the remainder to count backward or forward.
At what angle the hands of a clock are inclined when the time is 20 minutes past 4?
View Solution
At 4:00, the hour hand is at 120° (4 × 30°). At 20 minutes past 4, the hour hand moves further. In 20 minutes, the hour hand moves 10° (0.5° per minute). The minute hand is at 120° (20 × 6°). The angle between the two hands is 10°. Quick Tip: In clock-related problems, calculate the position of both hands in degrees and subtract the smaller angle from the larger one.
If A is the brother of the son of B's son, how is A related to B?
View Solution
A is the brother of B's grandson, so A is B's grandson. Quick Tip: For family relationship questions, break down the family tree to understand the relationships.
Six friends A, B, C, D, E and F are sitting around a round table facing the centre of the table. E is to the left of D, C is between A and B, and F is between E and A. Who is on the left of B?
View Solution
Step 1: From the given information, we know the following:
- E is to the left of D.
- C is between A and B.
- F is between E and A.
Step 2: Placing them on the table, we get the following arrangement:
E is left of D, and F is between E and A. C sits between A and B. The only remaining position for C is next to B. Thus, C is on the left of B. Quick Tip: In seating arrangement questions, try to visualize the positions step by step based on the given relations and constraints.
In which year the total number of cars of types A and B together was equal to that of types D and E together?
View Solution
From the table, we find that the total number of cars of types A and B together and types D and E together in 2019:
\[ A + B = 15000 + 10000 = 25000 \quad and \quad D + E = 5000 + 6000 = 11000 \]
Thus, the total production of types A and B equals types D and E in 2019. Quick Tip: For such questions, simply add the values of the required columns and compare.
The increase percentage of total production of all modes in 2023 to that of 2018 is:
View Solution
The total production in 2018 is 71000, and in 2023 it is 82000. The percentage increase is calculated as: \[ \frac{82000 - 71000}{71000} \times 100 = 15.5% \]
Thus, the increase percentage is 15.5%. Quick Tip: To calculate percentage increase, subtract the old value from the new value, divide by the old value, and multiply by 100.
In which year the production of all types of cars taken together was nearest to the average of total production during 2018-2023?
View Solution
The average production from 2018 to 2023 is calculated as: \[ \frac{71000 + 73000 + 75000 + 75000 + 80000 + 82000}{6} = 75833.33 \]
The production in 2019 is 73000, which is closest to the average. Quick Tip: When comparing numbers to an average, calculate the average first and then find the value closest to it.
The production of which type of cars was 25% of the total production of all types in 2022?
View Solution
The total production in 2022 is 80000. 25% of 80000 is: \[ 0.25 \times 80000 = 20000 \]
Looking at the table, we see that type E has 20000 cars produced in 2022. Therefore, type E is the correct answer. Quick Tip: To find the percentage of total production, multiply the total by the percentage value (in decimal form).
The decrease percentage of type C cars from 2022 to 2023 is:
View Solution
The number of type C cars in 2022 is 14000, and in 2023 it is 12000. The decrease percentage is calculated as: \[ \frac{14000 - 12000}{14000} \times 100 = 50% \]
Thus, the decrease percentage is 50%. Quick Tip: To calculate a decrease percentage, subtract the new value from the old value, divide by the old value, and multiply by 100.
How many know only Telugu and English?
View Solution
From the given information in the table, the total number of members who know only Telugu and English is 50.
Quick Tip: Look for exclusive groups in Venn diagram-based problems. The total number of members knowing specific combinations can be found by focusing on the exclusive categories.
What is the percentage of people in the community knowing Hindi and English only?
View Solution
The number of people who know only Hindi and English is 40. The total population is 300. So, the percentage is: \[ \frac{40}{300} \times 100 = 13.33% \]
Thus, the percentage of people who know only Hindi and English is 13.33%.
Quick Tip: To calculate percentage, divide the part by the whole and multiply by 100.
The number of members who do not know English is:
View Solution
The total number of people in the community is 300. From the table, the total number of people who know English is the sum of those knowing only English, those knowing English and Hindi, and those knowing English and Telugu. Using the data, the number of people who do not know English is: \[ 300 - Total number knowing English = 130 \]
Thus, 130 members do not know English.
Quick Tip: To find the number of people who do not belong to a group, subtract the total number in the group from the total population.
The number of persons who know only one of the three languages is:
View Solution
From the given information, the number of people who know only one language is calculated by adding the number of people who know only Hindi, only English, and only Telugu: \[ Only Hindi = 40, \quad Only English = 30, \quad Only Telugu = 40 \]
Thus, the total number of people who know only one language is: \[ 40 + 30 + 40 = 110 \]
So, 110 people know only one language. Quick Tip: For such questions, carefully examine the exclusive groups in the Venn diagram to find the total number of people knowing only one language.
The percentage of members not knowing Hindi is:
View Solution
The total number of people is 300. From the given data, the number of people who know Hindi is the sum of those knowing only Hindi, those knowing Hindi and English, those knowing Hindi and Telugu, and those knowing all three languages. The total number of people who do not know Hindi is: \[ 300 - Total number knowing Hindi = 120 \]
Thus, the percentage of people who do not know Hindi is: \[ \frac{120}{300} \times 100 = 40% \] Quick Tip: To calculate the percentage, subtract the group size from the total population and then divide by the total population. Multiply by 100 for percentage.
The calendar for the year 2007 will be the same for the following year:
View Solution
A calendar repeats itself after 11 years or 6 years depending on the leap year cycle. Since 2007 is not a leap year, the next calendar that will be the same as 2007 is 2018. Quick Tip: To find a year with the same calendar, check if the year is a common year or a leap year and then find the next year with the same weekday pattern.
What is the angle between the hour hand and minute hand at 3 PM?
View Solution
At 3 PM, the minute hand is at the 12th position (0°), and the hour hand is at the 3rd position (90°). Thus, the angle between them is 90°. Quick Tip: For calculating the angle between the hour and minute hand, use the fact that each hour represents 30° on the clock.
On which day of the week will India celebrate its 150th Independence Day?
View Solution
India's 150th Independence Day will fall on August 15, 2017. To find the day of the week, we can calculate the weekday for August 15, 2017, which is a Thursday. Quick Tip: To determine the weekday for a given date, you can use date calculation formulas or refer to reliable calendar tools.
Ramu ranks 7th from the top and 28th from the bottom in the class. How many students are there in the class?
View Solution
The total number of students is the sum of Ramu's rank from the top and from the bottom, minus 1 (since Ramu is counted twice): \[ 7 + 28 - 1 = 34 \]
Thus, there are 34 students in total. Quick Tip: To calculate the total number of people in a group, sum the ranks from both ends and subtract 1.
What was the day on 1st January, 1 A.D.?
View Solution
1st January, 1 A.D. was a Monday. Using date calculation algorithms or known historical references, we can determine this day. Quick Tip: You can use Zeller's Congruence or other algorithms to calculate the day of the week for any given date.
How many times do the hour and minute hands of the clock are perpendicular to each other in a day?
View Solution
The hour and minute hands are perpendicular to each other 22 times in 24 hours, not 24 times. There is a specific interval between each time the hands are perpendicular. Therefore, the correct answer is 20 times. Quick Tip: This question is based on the concept of clock angles and the number of times the hands of a clock become perpendicular within a 24-hour period.
At what time between 6 O'clock and 7 O'clock will the hands of a clock coincide?
View Solution
To find the time at which the hour and minute hands coincide, we use the formula: \[ Time = \frac{60}{11} \times difference in positions \]
For 6 O'clock to 7 O'clock, the time when the hands coincide is 6 hours 33 minutes. Quick Tip: For such questions, use the formula for calculating when the hands coincide and remember that the hands of the clock move 360° in 12 hours.
In how many different ways can the letters of the word BANANA be arranged?
View Solution
The total number of ways to arrange the letters of the word "BANANA" is given by the formula: \[ \frac{6!}{3!2!} \]
Where 6! accounts for the total letters and 3! and 2! account for the repetitions of 'A' and 'N' respectively.
Thus, the number of arrangements is: \[ \frac{720}{6 \times 2} = 60 \] Quick Tip: For such questions, use the formula for permutations of multiset objects: \[ \frac{n!}{k_1! \cdot k_2! \cdot \cdots \cdot k_r!} \] where \( n \) is the total number of objects and \( k_i \) is the factorial of the number of identical objects.
Given \( a*b = \frac{a^2 + b^2}{ab} \), then \( 1*(1*(1*1)) = ?
View Solution
Using the given expression \( a*b = \frac{a^2 + b^2}{ab} \), we can calculate \( 1*(1*(1*1)) \) as follows: \[ 1*1 = \frac{1^2 + 1^2}{1 \times 1} = \frac{2}{1} = 2 \]
Then: \[ 1*(1*1) = 1*2 = \frac{1^2 + 2^2}{1 \times 2} = \frac{1 + 4}{2} = 2.5 \]
Finally: \[ 1*(1*(1*1)) = 1*2.5 = \frac{1^2 + 2.5^2}{1 \times 2.5} = \frac{1 + 6.25}{2.5} = 2.9 \] Quick Tip: To solve problems like this, evaluate each operation step by step using the given mathematical expression.
For real numbers \( a \) and \( b \), if \( a*b = (a - b)^4 \), then \( (62)*(65) = ?
View Solution
Given the operation \( a*b = (a - b)^4 \), we can solve for \( (62)*(65) \) as follows: \[ (62)*(65) = (62 - 65)^4 = (-3)^4 = 81 \] Quick Tip: For this type of operation, simplify the subtraction first, then apply the exponent.
Choose the meaning of the underlined word
There is no \underline{gainsaying that the country is in difficulties.
View Solution
The word "gainsaying" means denying or contradicting. It refers to the act of stating that something is not true. Quick Tip: "Gainsaying" often appears in formal contexts, and it refers to denying or disputing something.
Choose the correct meaning of the following word "Luxuriant"
View Solution
"Luxuriant" means abundant or rich in growth, especially in plants. It refers to something thriving or flourishing. Quick Tip: "Luxuriant" is used to describe something that grows in abundance, especially plants or vegetation.
Choose the correct meaning of the following word "Camouflage"
View Solution
"Camouflage" refers to the act of disguising the appearance of something to make it blend in with its surroundings. It is often used in military contexts. Quick Tip: "Camouflage" is used for hiding something by changing its appearance to match its surroundings.
Choose the correct meaning of the following word \textbf{Prophylactic}
View Solution
The word "prophylactic" refers to something intended to prevent disease or harmful effects. The correct meaning is "Preventive."
Quick Tip: "Prophylactic" is often used in medical contexts to refer to actions or treatments meant to prevent illness or disease.
Choose the correct meaning of the following word \textbf{Belligerent}
View Solution
The word "belligerent" refers to someone who is hostile or aggressive. The correct meaning is "Hostile."
Quick Tip: When you encounter the word "belligerent," think of someone involved in conflict or hostility.
Choose the correct meaning of the following word \textbf{Construe}
View Solution
The word "construe" means to interpret or analyze the meaning of something. The correct meaning is "Interpret."
Quick Tip: "Construe" is often used when analyzing or explaining the meaning of a statement or action.
Fill in the blank with suitable word: The science that deals with the structure and position of body parts is called ____.
View Solution
Anatomy is the branch of science that deals with the structure and position of body parts. Physiology, on the other hand, deals with the functions of body parts, while dermatology focuses on the skin, and cardiology concerns the heart.
Quick Tip: Remember, anatomy is about the structure, while physiology is about function. Keep these two branches distinct to avoid confusion.
Fill in the blank with suitable word: The workers felt happy as their salary was ____.
View Solution
The correct word to complete the sentence is "enhanced," as it fits the context of the workers feeling happy about their salary increase. "Reduced" would not fit, as it would make the workers unhappy, and "delayed" or "denied" would imply negative circumstances.
Quick Tip: In fill-in-the-blank questions, think about the overall context and choose the word that logically fits the sentiment conveyed.
Fill in the blank with suitable word: The melody of a song can ____ infants and animals, alike.
View Solution
The correct word here is "enchant," as the melody of a song has the power to captivate or enchant both infants and animals. "Trouble" and "inconvenience" would not make sense in this context, and "enfeeble" means to weaken, which is also inappropriate here.
Quick Tip: When choosing the right word, consider the emotional or sensory impact of the action described. In this case, the song’s melody is likely to captivate or enchant.
Their appeal was rejected as it had no ____
View Solution
In the context of an appeal, "substance" refers to the lack of significant or meaningful content, which can lead to rejection.
Quick Tip: When an appeal is rejected, it is often due to the lack of important substance or grounds, not trivial reasons.
The rise in prices leads to what is often called ____
View Solution
Inflation refers to the general increase in prices over time, which reduces purchasing power. Hyper-flation refers to an extremely high rate of inflation, while depreciation involves the decrease in value of an asset.
Quick Tip: Inflation is the term used for general price increases, whereas deflation refers to a decrease in prices.
He wasted all the money given by his father as he was ____
View Solution
A spendthrift is someone who spends money recklessly or extravagantly. A frugal person is one who is careful with money. Transparent refers to clarity, and balanced refers to a steady approach to life.
Quick Tip: A spendthrift wastes money, while a frugal person saves and spends wisely.
They became bankrupt as they had more ___ than assets.
View Solution
The phrase refers to bankruptcy, which occurs when liabilities exceed assets. A company or individual becomes bankrupt when their debts (liabilities) surpass their assets. Therefore, the correct word to complete the sentence is "Liabilities."
Quick Tip: In financial terms, liabilities are the debts that a company or individual owes. Understanding the balance between assets and liabilities is essential for financial planning.
A fool and his money are easily ___
View Solution
The common proverb "A fool and his money are easily parted" means that someone who is foolish will easily lose or waste their money. The word "parted" fits the context, as it refers to the separation of the money from the fool.
Quick Tip: Proverbs often contain universal truths, and understanding them can improve your vocabulary and comprehension skills.
Fill in the blank with suitable word
% Sentence
The director of the company ____ to talk to a mere temporary employee.
View Solution
The correct word to complete the sentence is "condescended" because it means to lower oneself to a less important level, which fits with the context of the director talking to a mere temporary employee.
Quick Tip: In fill-in-the-blank questions, consider the meaning of the sentence and choose the word that fits the context appropriately.
Fill in the blank with suitable word
% Sentence
He was astonished ____ his failure.
View Solution
The correct word to complete the sentence is "with." The phrase "astonished with" is commonly used when referring to being shocked or surprised by something. Therefore, the sentence should read, "He was astonished with his failure."
Quick Tip: When filling in the blanks with prepositions, consider common collocations or expressions where the preposition is typically used.
Fill in the blank with suitable word
% Sentence
We have been living here ____ ten years.
View Solution
The correct preposition is "for." The phrase "for ten years" is used to indicate the duration of time the action has been happening. Therefore, the sentence should read, "We have been living here for ten years."
Quick Tip: "When discussing the duration of an action that started in the past and continues into the present, use 'for' followed by a period of time."
Fill in the blank with suitable word
% Sentence
The birds are chirping in the trees, ____?
View Solution
The correct question tag is "aren’t they" because it matches the plural subject "birds" and the positive statement. The sentence should read, "The birds are chirping in the trees, aren’t they?"
Quick Tip: In question tags, make sure the auxiliary verb agrees with the subject in number and tense.
Fill in the blank with suitable word
% Sentence
My brother or my sister ____ to the marriage.
View Solution
The subject "my brother or my sister" refers to a singular person, and it takes the singular verb "is coming." However, since we are dealing with an either/or situation, the verb in this context should be plural, so the correct choice is "are coming."
Quick Tip: For sentences with compound subjects like "or," consider the subject closest to the verb to determine the appropriate verb form.
Fill in the blank with suitable word
% Sentence
The message was sent ____ post.
View Solution
The correct preposition is "by" in this case. We say that something was sent "by post" to mean it was sent using postal mail. Therefore, the sentence should read, "The message was sent by post."
Quick Tip: In phrases like "sent by post," the preposition "by" is commonly used to indicate the method of sending something.
Fill in the blank with suitable word
% Sentence
The bus was ready ____ the foot of the temple.
View Solution
The correct preposition here is "upon," which is used to indicate position or location in phrases like "at the foot of" or "upon the foot of." Thus, the sentence should read, "The bus was ready upon the foot of the temple."
Quick Tip: In location-based phrases, "upon" is often used to show a more formal or poetic position relative to a landmark or base.
Fill in the blank with suitable word
% Sentence
You ____ are to blame for this.
View Solution
The correct answer is "you." The sentence should read, "You are to blame for this," which is the correct grammatical structure. "Yourself" is used for reflexive actions, "your" is a possessive adjective, and "yours" is a possessive pronoun, but none of these fit the structure here.
Quick Tip: In fill-in-the-blank questions, consider the context and grammatical structure of the sentence to choose the correct word.
Fill in the blank with suitable word
% Sentence
You are not ill, ____?
View Solution
The correct question tag for a positive sentence like "You are not ill" is "aren’t you?" The auxiliary verb "are" is used with the subject "you" and the question tag must be in the negative form, hence "aren’t you."
Quick Tip: For question tags, if the statement is positive, use a negative question tag. If the statement is negative, use a positive question tag.
Fill in the blank with suitable word
% Sentence
This locality ____ different minerals.
View Solution
The correct phrase is "abounds in," which is used to indicate the presence of a large quantity of something in a place or area. Therefore, the sentence should read, "This locality abounds in different minerals."
Quick Tip: "Abound" is commonly followed by the preposition "in" to indicate an abundance of something.
Fill in the blank with suitable word
% Sentence
He has a fascination ____ music.
View Solution
The correct preposition to use with "fascination" is "for." We say someone has a fascination for something, in this case, music. Thus, the correct sentence is, "He has a fascination for music."
Quick Tip: When using "fascination," remember it is usually followed by "for" to indicate the object of the fascination.
Fill in the blank with suitable word
% Sentence
The nurse is attending ____ the patient.
View Solution
The correct preposition is "with" because we say that someone is "attending to" or "attending with" another person in a care setting. Thus, the sentence should read, "The nurse is attending with the patient."
Quick Tip: In medical contexts, "attending with" is used to indicate caring for or accompanying someone.
Fill in the blank with suitable word
% Sentence
He knows Telugu ____ Hindi.
View Solution
The correct phrase is "as well as" because it is used to link two things that the subject is familiar with or able to do. The sentence should read, "He knows Telugu as well as Hindi."
Quick Tip: The phrase "as well as" is commonly used to link two subjects or objects that are equally true or valid.
Fill in the blank with suitable word
% Sentence
There was a lot of traffic, ____?
View Solution
The correct choice is (3) "wasn't there" because the sentence is a negative statement ("There was a lot of traffic"), and the question tag must match the verb form and be negative. Hence, "wasn't there" is the appropriate tag.
Quick Tip: In question tags, if the main sentence is in the past tense, use the past tense in the question tag as well.
Fill in the blank with suitable word
% Sentence
I will see you ____ Friday.
View Solution
The correct preposition is "on." We say "on Friday" when referring to a specific day of the week. Thus, the sentence should read, "I will see you on Friday."
Quick Tip: For days of the week, we typically use the preposition "on" (e.g., on Monday, on Tuesday).
Fill in the blank with suitable word
% Sentence
Surya is going away ____ a week in September.
View Solution
The correct preposition is "for" because it indicates the duration of Surya's absence in September. Thus, the sentence should read, "Surya is going away for a week in September."
Quick Tip: Use "for" to express the duration of time something will happen.
Fill in the blanks with suitable word
% Sentence
They saw ____ lion in ____ zoo.
View Solution
The correct article to use before "lion" is "a" because it refers to one unspecified lion, and the definite article "the" is used before "zoo" because it refers to a specific zoo. Thus, the sentence should read, "They saw a lion in the zoo."
Quick Tip: Use "a" before singular, countable nouns when mentioning something for the first time, and "the" when referring to something specific.
Fill in the blank with suitable word
% Sentence
I prefer coffee ____ tea.
View Solution
The correct preposition is "to" when comparing preferences. In this case, "I prefer coffee to tea" is the appropriate sentence.
Quick Tip: When comparing two things with the verb "prefer," use the preposition "to."
Choose the antonym for ‘convex’.
View Solution
The antonym of "convex" is "concave." Convex refers to an outward bulging shape, while concave refers to an inward curving shape. Thus, the correct answer is "concave."
Quick Tip: "Convex" and "concave" are opposite terms commonly used in geometry to describe the shape of curves or surfaces.
Choose the correct form of positive degree for the following sentence from the given options:
% Sentence
He drives the car faster than anyone else.
View Solution
In the positive degree, the comparison is made between the subject and others. The correct form is "No one drives the car as fast as he does," indicating that his speed is equal to or faster than anyone else's.
Quick Tip: Use the positive degree to show equality in comparison.
Choose the correct form of indirect speech for the following sentence from the given options:
% Sentence
And then I thought, “Well, does he really mean it?”
View Solution
In indirect speech, the reporting verb is changed to the past tense, and the direct question is rephrased without a question mark. The correct sentence is "And then I wondered whether he really meant it."
Quick Tip: In indirect speech, we usually change the tense from present to past and remove the question mark.
Document that has a list of items to be discussed at a meeting is called.
View Solution
An agenda is a document that lists all the items to be discussed in a meeting. It is a plan or outline that is followed during a meeting. The other options do not fulfill this purpose.
Quick Tip: Remember, the agenda is always prepared before the meeting and outlines the topics to be covered.
Which of the following produces the best quality graphics reproduction?
View Solution
Plotters are specialized printers designed for high-quality graphical output, such as vector graphics or detailed diagrams. They provide superior quality in terms of precision and color accuracy compared to other types of printers like laser and inkjet printers. Laser printers and inkjet printers are generally used for text printing and general purposes, while dot matrix printers are older technology that produces lower-quality graphics.
Quick Tip: For high-quality graphics reproduction, plotters are the best option, especially when working with intricate designs and vector graphics.
The design that helps hackers is called
View Solution
The term "trojan horse" refers to a type of malicious software that pretends to be a legitimate program or file. Once executed, it can provide unauthorized access to the system and allow hackers to manipulate or steal data.
Quick Tip: Be aware of Trojan horses, which can disguise themselves as trustworthy software. Always verify software before downloading or executing it.
A symbol indicating retrieval of data is a/an
View Solution
The "hour glass" symbol is commonly used in computer systems to indicate that the system is busy and that data is being retrieved. It is typically represented by an hourglass icon.
Quick Tip: Pay attention to system icons like the hourglass, as they indicate processing time or waiting for a response.
Planning teams simulate the role of information technology in various hypothetical business situation is known
View Solution
Scenario approach involves simulating various hypothetical business situations and assessing the role of information technology in addressing these scenarios. It helps organizations prepare for different potential outcomes and plan effectively.
Quick Tip: Scenario planning is valuable for forecasting and strategizing in uncertain business environments.
What is Bounce Rate in Business?
View Solution
Bounce rate is a metric that represents the percentage of visitors who visit a website and leave without interacting with any other pages. This is typically related to the frequency of visitors leaving without engagement, which is often an indicator of the quality of a website's content.
Quick Tip: Focus on website metrics such as bounce rate to assess the effectiveness of the content and engagement.
Fair Trade means
View Solution
Fair Trade refers to an international movement that seeks to ensure that producers in developing countries get a fair deal for their products. It promotes ethical business practices, providing better prices and fairer trading terms for producers.
Quick Tip: In the context of international trade, fair trade supports equal opportunities and social and economic justice.
Grapevine is a term used for
View Solution
The term "grapevine" refers to informal, unofficial communication that takes place in an organization. It is often a form of communication through word of mouth, without any formal structure or regulation.
Quick Tip: When considering internal communication within an organization, informal communication often spreads quickly and can sometimes be more influential than formal channels.
The dividend is paid on ____
View Solution
Dividends are payments made by a corporation to its shareholders, typically out of its profits. These payments are made on company shares, as shareholders are entitled to receive dividends based on the number of shares they own. Other financial instruments like bonds or debentures do not receive dividends, but rather interest payments.
Quick Tip: Focus on the nature of the financial instruments when identifying which one yields dividends.
Full form of Wi-Fi is ____
View Solution
Wi-Fi stands for Wireless Fidelity, a technology that allows devices to connect to the internet without using wires, using radio waves for data transmission. It is a widely used technology for wireless networking.
Quick Tip: Wi-Fi technology is often used in various devices such as laptops, smartphones, and routers to enable wireless communication.
Demonetization refers to ____
View Solution
Demonetization refers to the act of removing a currency unit from circulation, usually by the government, thereby ceasing its status as legal tender. It typically involves withdrawing existing currency notes and/or coins from use and replacing them with new ones or introducing new forms of currency.
Quick Tip: Demonetization is usually done to control black money, counterfeit currency, or inflation.
Who is the Chief Executive Officer of Niti Ayog?
View Solution
B.V.R Subrahmanyam is the Chief Executive Officer of Niti Ayog.
Quick Tip: When learning about governmental positions, focus on key leadership roles like CEOs of major organizations such as Niti Ayog.
Crypto currency refers to
View Solution
Cryptocurrency is a digital or virtual form of currency that uses encryption techniques to regulate the creation of new units and secure transactions. It operates independently of central banks or financial institutions.
Quick Tip: Remember that cryptocurrency is not controlled by any central authority, making it a decentralized form of currency.
What is the full form of NPCI?
View Solution
The full form of NPCI is National Payments Corporation of India. It is an umbrella organization for all retail payment systems in India.
Quick Tip: NPCI is critical for ensuring secure and efficient digital payments in India, including platforms like UPI and IMPS.
What is the storage that refers to the remote storage facility available anywhere on the internet?
View Solution
Cloud storage is a remote storage service that allows data to be stored and accessed over the internet. It offers the ability to store files remotely and access them from anywhere using an internet connection.
Quick Tip: Cloud storage is becoming essential for businesses and individuals who need to access and share large amounts of data quickly and securely.
What is the effect of fear on humans?
View Solution
Fear often restricts the ability to think freely and make rational decisions. It can also hinder the development of intelligence as it creates mental barriers.
Quick Tip: Fear can have a significant impact on cognitive function, so it's important to overcome fear to develop clarity and creativity in thought.
The aim of education is to make us realize the need of ____
View Solution
The purpose of education goes beyond acquiring job-related skills; it is also about gaining the freedom to explore ideas and make independent decisions.
Quick Tip: When pursuing education, focus not just on exams and jobs, but also on gaining the freedom to think critically and live meaningfully.
When we are young, we should ____
View Solution
While getting an education and pursuing a career is important, seeking the meaning of life is essential for personal fulfillment. This should be explored early in life to create a meaningful future.
Quick Tip: Seek a balanced approach to life: focus not only on career but also on understanding the purpose and direction of your life.
Education helps us realize the ____
View Solution
Education helps us realize the importance of freedom in all walks of life, which is essential for personal growth and societal progress.
Quick Tip: When analyzing the purpose of education, focus on how it empowers individuals and promotes the values necessary for progress and personal freedom.
The passage is about:
View Solution
The passage emphasizes the role of freedom and how it is necessary for individuals to develop their true potential.
Quick Tip: When studying a passage, pay attention to the underlying theme being conveyed, especially when the topic revolves around personal development and societal values like freedom.
Powerful rulers who are sentimental decide the policies of the nations:
View Solution
The statement implies that powerful rulers who are influenced by sentiment and emotions may make decisions without relying on the rational guidance of science. Such decisions can sometimes be detrimental to the progress of a nation.
Quick Tip: When analyzing the impact of sentiment in leadership, consider the balance between logic and emotion, especially in decision-making.
If a man were to say "I hate the human race, and I think it would be a good thing if it were exterminated," we could say, "Well, my dear sir, let us begin the process with you". What does the statement mean?
View Solution
The statement implies that those who advocate for the destruction of mankind should be the first to undergo such destruction. It emphasizes a paradox where the person proposing the harm is a part of the harm itself.
Quick Tip: Be cautious when expressing opinions about others, as the consequences of such actions may come back to impact you directly.
To do good or harm depends on ____
View Solution
The ability to do good or harm is not just a matter of having scientific knowledge or wealth; rather, it is rooted in the wisdom with which that knowledge and wealth are applied. Wisdom helps individuals and societies make decisions that promote the welfare of all.
Quick Tip: Remember, knowledge alone isn't enough; wisdom is needed to ensure that knowledge is used for the common good.
We cannot insure our own prosperity except by____
View Solution
Our own prosperity depends on our actions. By focusing on our well-being and personal responsibility, we can ensure a better future for ourselves. The other options don't offer a solution to personal prosperity.
Quick Tip: To secure a prosperous future, focus on self-care, responsibility, and personal growth.
Science can achieve many ends; but it cannot solve____
View Solution
Science can solve many technical and practical problems, but ethical problems require wisdom, morality, and human judgment, which science alone cannot provide.
Quick Tip: When approaching ethical dilemmas, always consider human values, moral judgment, and personal beliefs, not just scientific data.
What was the first impression of the author about the visitor?
View Solution
The author initially thought that the visitor was an Egyptian peasant because of his appearance, including his dark robe and turban.
Quick Tip: Pay attention to the details about the visitor’s appearance mentioned in the passage to understand the author's first impression.
What was the name of the visitor?
View Solution
The name of the visitor was Ahmad, as mentioned in the passage.
Quick Tip: Focus on the introduction of the visitor in the passage, where his name is revealed.
How did the speaker and Ahmad respond once they recognized each other?
View Solution
Once they recognized each other, both the speaker and Ahmad emotionally embraced, sobbing due to the years of separation.
Quick Tip: Look for emotional cues in the passage to understand the depth of their reunion.
What is 'Edfu' in the passage?
View Solution
'Edfu' is referred to as a town in the passage, highlighting its historical significance.
Quick Tip: When reading, note the geographical and cultural references to understand the context better.
What is the theme of the passage?
View Solution
The passage revolves around reminiscing about past emotions and the deep connection between individuals from different walks of life.
Quick Tip: Explore the underlying emotions and connections in any passage to better understand the theme.
What is a key characteristic of India’s business environment?
View Solution
India's business environment is characterized by complex cultural diversity, which influences consumer behavior, product development, and market strategies.
Quick Tip: When analyzing India’s market, always consider the diverse cultural factors and regional differences that shape consumer needs.
Which initiative aimed to simplify taxation in India?
View Solution
The Goods and Services Tax (GST) was implemented to simplify taxation in India by eliminating multiple taxes and creating a unified tax structure across the country.
Quick Tip: When studying tax reforms, focus on understanding how GST streamlines processes and ensures a single tax regime.
Which Indian city is often referred to as the ‘Silicon Valley of India’?
View Solution
Bangalore, often referred to as the "Silicon Valley of India," is a major hub for IT companies, startups, and innovation, making it a key player in the Indian tech industry.
Quick Tip: When studying India’s technology landscape, focus on Bangalore's pivotal role in driving innovation and tech entrepreneurship.
What challenges do businesses face due to India's cultural diversity?
View Solution
Due to the vast cultural diversity in India, businesses often face challenges such as language barriers when trying to communicate and interact with different regional groups. These differences in language and cultural preferences can impact marketing strategies, customer relations, and overall business operations.
Quick Tip: When planning a business strategy in India, it is crucial to account for regional variations in language and culture.
What initiative aims to boost manufacturing in India?
View Solution
The "Make in India" initiative was launched to encourage national and multinational companies to manufacture their products in India. This initiative aims to boost the manufacturing sector, create job opportunities, and improve India's overall industrial infrastructure.
Quick Tip: "Make in India" is a key initiative for increasing India's manufacturing capacity and promoting industrial growth.
What is a key characteristic of India's business environment?
View Solution
India's business environment is characterized by complex cultural diversity, with various languages, traditions, and customs across its regions. This diversity can create both challenges and opportunities for businesses, as understanding and adapting to local cultures can lead to greater market success.
Quick Tip: When conducting business in India, understanding regional cultural differences is essential for success.
Arithmetical Ability - If 17.28\texttt{x} = 200, then the value of x is
View Solution
We are given the equation: \[ 17.28 \times x = 200 \]
To solve for \(x\), we divide both sides by 17.28: \[ x = \frac{200}{17.28} \] \[ x = 0.12 \] Quick Tip: For solving such problems, always check the units and use the correct method of isolating the variable.
Arithmetical Ability - If \(\sqrt{15} = 3.88\), then \(\sqrt[3]{15}\) is
View Solution
We are given that \( \sqrt{15} = 3.88 \). To estimate the cube root of 15, we use estimation methods and find that: \[ \sqrt[3]{15} \approx 1.63 \] Quick Tip: For cube roots, try estimating using nearby perfect cubes and check if they match the given values closely.
Arithmetical Ability - If \(\sqrt{x^2} \times 15^2 = 5^2 \times 3^2\), then x =
View Solution
We are given the equation: \[ \sqrt{x^2} \times 15^2 = 5^2 \times 3^2 \]
Simplify both sides: \[ x \times 225 = 25 \times 9 \] \[ x \times 225 = 225 \]
Now, divide both sides by 225: \[ x = \frac{225}{225} \] \[ x = 12 \] Quick Tip: When solving for x in equations with exponents, always simplify both sides step by step and keep track of all operations carefully.
H.C.F. of \(\frac{1}{2}\), \(\frac{3}{5}\), \(\frac{7}{8}\), \(\frac{9}{10}\) is
View Solution
The HCF of fractions is calculated by finding the HCF of the numerators and the LCM of the denominators.
HCF of \(1, 3, 7, 9\) is \(1\).
LCM of \(2, 5, 8, 10\) is \(120\).
Therefore, the HCF of the given fractions is \(\frac{1}{120}\).
Quick Tip: When calculating HCF of fractions, find the HCF of numerators and LCM of denominators.
The least perfect square number which is divisible by 21, 36 and 66 is
View Solution
We need to find the least common multiple (LCM) of 21, 36, and 66, and then find the least perfect square divisible by the LCM.
LCM of \(21, 36, 66\) is \(213444\).
Therefore, the least perfect square divisible by 21, 36, and 66 is \(213444\).
Quick Tip: To find the least perfect square divisible by several numbers, first calculate the LCM and then adjust it to be a perfect square.
Which number should be there in place of * so that 593248* is divisible by 8?
View Solution
To check divisibility by 8, the last three digits of the number must be divisible by 8.
The number \(593248*\) is divisible by 8 when the last three digits form a number divisible by 8.
Therefore, the digit to replace * is \(3\) to make it divisible by 8.
Quick Tip: To check divisibility by 8, consider the last three digits of the number and verify divisibility.
Arithmetical Ability -
If \(\dfrac{9^2 \times 16^8}{3^{16}}\) is ____
View Solution
We have the expression:
\[ \frac{9^2 \times 16^8}{3^{16}} = \frac{3^4 \times 2^{32}}{3^{16}} = \frac{2^{32}}{3^{12}} = \frac{16}{81} \]
Thus, the correct answer is \(\dfrac{16}{81}\). Quick Tip: When solving exponentiation problems, simplify the exponents of like bases first before performing the operation.
If \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{7}\), then \(x + y + z\) =
View Solution
We are given that \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{7}\).
Let the common value be \(k\), so we have the following relations: \[ x = 3k, \quad y = 4k, \quad z = 7k \]
Now, we need to calculate the value of \(x + y + z\): \[ x + y + z = 3k + 4k + 7k = 14k \]
Since we know that \(x = \dfrac{3}{7}, y = \dfrac{4}{7}, z = \dfrac{7}{7}\), we can substitute these values back into the equation for \(x + y + z\): \[ x + y + z = 2 \]
Thus, the correct value for \(x + y + z\) is 2.
Quick Tip: When you encounter equations of the form \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\), express each variable in terms of a common ratio, like \(k\), to simplify solving.
If \(18 : x = x : 8\), then \(x =\)
View Solution
We are given the proportion \(18 : x = x : 8\).
This implies that: \[ \frac{18}{x} = \frac{x}{8} \]
Cross multiplying, we get: \[ 18 \times 8 = x^2 \] \[ 144 = x^2 \]
Taking the square root of both sides: \[ x = \sqrt{144} \] \[ x = 12 \]
Thus, the value of \(x\) is 12.
Quick Tip: When solving proportions, use cross multiplication to simplify the equation into a quadratic form, then solve for the variable.
What must be added to each term of the ratio \(7:13\) so that the ratio becomes \(2:3\)?
View Solution
Let the number to be added to both terms of the ratio be \(x\).
Then the new ratio becomes: \[ \frac{7 + x}{13 + x} = \frac{2}{3} \]
Now, we solve this equation by cross-multiplying: \[ 3(7 + x) = 2(13 + x) \]
Expanding both sides: \[ 21 + 3x = 26 + 2x \]
Subtract \(2x\) from both sides: \[ 21 + x = 26 \]
Subtract 21 from both sides: \[ x = 5 \]
Thus, 5 must be added to each term of the ratio to make the ratio \(2:3\).
Quick Tip: When solving problems involving ratios, convert the ratio into an equation and solve for the unknown by cross-multiplying.
The two numbers are in the ratio 5:7. Their difference is 10. Then the sum of numbers is
View Solution
Let the two numbers be \( 5x \) and \( 7x \). Their difference is given as: \[ 7x - 5x = 10 \] \[ 2x = 10 \quad \Rightarrow \quad x = 5 \]
Therefore, the two numbers are \( 5x = 25 \) and \( 7x = 35 \), and their sum is: \[ 25 + 35 = 60 \] Quick Tip: To solve ratio and proportion problems, express the numbers in terms of a variable and use the given conditions to find the variable's value.
The speeds of three cars are in the ratio 2:3:4. The ratio between the time taken by them to travel the same distance is
View Solution
Since time and speed are inversely proportional when the distance is constant, the ratio of times is the inverse of the ratio of speeds.
Thus, the ratio of times is \( \frac{1}{2} : \frac{1}{3} : \frac{1}{4} \), which simplifies to \( 6 : 4 : 3 \). Quick Tip: When dealing with speeds and times, remember that they are inversely proportional when the distance is constant.
If the digits of a given two-digit number are reversed, the number is equal to 9 less than 3 times the original number. If the difference between these two numbers is 45, find the original number.
View Solution
Let the original number be \( 10a + b \) where \( a \) and \( b \) are the tens and ones digits, respectively. The reversed number is \( 10b + a \).
According to the problem, the equation becomes: \[ 10b + a = 3(10a + b) - 9 \]
Simplifying, we get: \[ 10b + a = 30a + 3b - 9 \] \[ 7b - 29a = -9 \]
Additionally, the difference between the numbers is given as 45: \[ |10a + b - (10b + a)| = 45 \]
Solving this system of equations, we find \( a = 4 \) and \( b = 5 \), so the original number is 45. Quick Tip: When solving problems involving two-digit numbers and their digits, express the number in terms of its digits and set up equations accordingly.
If \( x \times 15 = 37.5% \) of 220, then \( x \) is
View Solution
We are given that \( x \times 15 = 37.5% \) of 220, so: \[ x \times 15 = \frac{37.5}{100} \times 220 \]
Simplifying: \[ x \times 15 = 82.5 \] \[ x = \frac{82.5}{15} = 5.5 \] Quick Tip: When solving percentage problems, first convert the percentage into a fraction and then solve the equation.
X% of Y + Y% of X =
View Solution
We know that \( X% \) of \( Y \) is \( \frac{X \times Y}{100} \) and \( Y% \) of \( X \) is also \( \frac{Y \times X}{100} \). Therefore: \[ X% \, of \, Y + Y% \, of \, X = \frac{X \times Y}{100} + \frac{Y \times X}{100} = \frac{2XY}{100} = Y% \, of \, X \] Quick Tip: When solving percentage problems involving both variables, remember that order doesn't matter due to the commutative property of multiplication.
Subtracting 6% of a number is equivalent to multiplying by how much.
View Solution
Subtracting 6% of a number is equivalent to multiplying the number by \( 100% - 6% = 94% \), or \( 0.94 \). Therefore: \[ New number = Original number \times 0.94 \] Quick Tip: When subtracting a percentage from a number, multiply by the complement of the percentage (i.e., \( 100% - percentage \)).
If A's salary is 30% less than that of B. Then how much percentage is B's salary more than that of A?
View Solution
Let A's salary be \( x \) and B's salary be \( y \). We know that A's salary is 30% less than B's, so: \[ x = y - 0.30y = 0.70y \]
Now, we calculate the percentage increase from A's salary to B's salary: \[ Percentage increase = \frac{y - x}{x} \times 100 = \frac{y - 0.70y}{0.70y} \times 100 = \frac{0.30y}{0.70y} \times 100 = 42\frac{6}{7}% \] Quick Tip: To find the percentage increase between two values, subtract the smaller value from the larger one, divide by the smaller value, and multiply by 100.
By selling 36 mangoes, a vendor loses the selling price of 4 mangoes. His loss percent is
View Solution
Let the cost price of each mango be \( C \) and the selling price of each mango be \( S \). The vendor loses the selling price of 4 mangoes when selling 36, so: \[ Loss = 4S \]
The total cost price for 36 mangoes is: \[ Total Cost Price = 36C \]
The total selling price for 36 mangoes is: \[ Total Selling Price = 36S \]
The loss percentage is: \[ Loss Percentage = \frac{Loss}{Total Cost Price} \times 100 = \frac{4S}{36C} \times 100 = 10% \] Quick Tip: When calculating loss percentage, use the formula \( \frac{Loss}{Cost Price} \times 100 \).
Subhas purchased a TV at \( \frac{4}{5} \)th of its selling price and sold it at 8% more than its original selling price. Then what is his gain percent?
View Solution
Let the selling price of the TV be \( S \). Subhas purchases the TV at \( \frac{4}{5} \times S \). He sells it at \( 8% \) more than the original price, so the selling price is: \[ New Selling Price = S + 0.08S = 1.08S \]
The gain is: \[ Gain = 1.08S - \frac{4}{5}S = \frac{1}{5}S \]
The gain percentage is: \[ Gain Percentage = \frac{Gain}{Cost Price} \times 100 = \frac{\frac{1}{5}S}{\frac{4}{5}S} \times 100 = 8% \] Quick Tip: When selling at a profit, use the formula \( \frac{Gain}{Cost Price} \times 100 \) to find the gain percentage.
P, Q, and R entered into a partnership, and their capitals are in the proportion of \( 1 : \frac{1}{2} : \frac{3}{4} \). P is withdrawing half of his capital at the end of 4 months. Out of a total annual profit of Rs. 847, P's share is
View Solution
Let the capitals of P, Q, and R be \( 1x \), \( \frac{1}{2}x \), and \( \frac{3}{4}x \), respectively. P withdraws half of his capital at the end of 4 months, so P's effective capital for the 12 months is: \[ P's capital = 1x \times 4 + \frac{1}{2}x \times 8 = 4x + 4x = 8x \]
Similarly, Q's effective capital is: \[ Q's capital = \frac{1}{2}x \times 12 = 6x \]
R's effective capital is: \[ R's capital = \frac{3}{4}x \times 12 = 9x \]
The total effective capital is: \[ Total Capital = 8x + 6x + 9x = 23x \]
P's share in the total profit is: \[ P's share = \frac{8x}{23x} \times 847 = \frac{8}{23} \times 847 = 280 \] Quick Tip: In partnership problems, use the concept of effective capital based on time to calculate the share of profit.
‘A’ can finish a work in 6 days. ‘B’ is 60% more efficient than ‘A’. Then how many days will ‘B’ take to complete the same work?
View Solution
Let the work done by ‘A’ per day be \( \frac{1}{6} \). Since ‘B’ is 60% more efficient than ‘A’, the work done by ‘B’ per day is \( 1.6 \times \frac{1}{6} = \frac{8}{30} = \frac{4}{15} \). Therefore, the number of days ‘B’ will take is: \[ Days taken by B = \frac{1}{\frac{4}{15}} = 3.75 \approx 4 \] Quick Tip: When efficiency is given as a percentage more than another's efficiency, multiply by \( 1 + percentage increase \) to find the rate of work.
A and B entered into a partnership. A invests Rs 16,000 for 8 months and B remains in the business for 4 months only. Out of a total profit, B claims \( \frac{3}{4} \)th of the profit, then B's contribution is
View Solution
Let the capital of A be Rs. 16,000 for 8 months, and for B, since he stays for only 4 months, the capital of B is Rs. 16,000 for 4 months. The effective capitals of A and B are: \[ A's Capital = 16,000 \times 8 = 1,28,000 \] \[ B's Capital = 16,000 \times 4 = 64,000 \]
Total capital = \( 1,28,000 + 64,000 = 1,92,000 \).
Since B claims \( \frac{3}{4} \)th of the profit, B’s share is: \[ B's Share = \frac{64,000}{1,92,000} \times \frac{3}{4} \times 847 = 2,56,000 \] Quick Tip: For partnership problems, calculate effective capital by multiplying the investment amount by the time, and then find the profit share based on this.
A pump can fill a tank with water in 16 minutes and another can empty it in 8 minutes. If the tank is already half full and both the taps are opened together, the tank will be
View Solution
The rate of filling the tank is \( \frac{1}{16} \) per minute and the rate of emptying the tank is \( \frac{1}{8} \) per minute. Together, the effective rate of filling the tank is: \[ \frac{1}{16} - \frac{1}{8} = \frac{1}{16} - \frac{2}{16} = -\frac{1}{16} \]
Since the tank is being emptied, it will take \( 16 \) minutes to empty the tank. Quick Tip: When two operations are happening simultaneously (e.g., filling and emptying), subtract the rates to find the net effect.
If two pipes function simultaneously, the reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours does the faster pipe take to fill the reservoir?
View Solution
Let the time taken by the slower pipe be \( x \) hours. Then the faster pipe takes \( x - 10 \) hours. The combined rate of both pipes is \( \frac{1}{12} \), and the rate of the slower pipe is \( \frac{1}{x} \) and the faster pipe is \( \frac{1}{x - 10} \). Therefore: \[ \frac{1}{x} + \frac{1}{x - 10} = \frac{1}{12} \]
Solving this equation, we find \( x = 30 \), meaning the faster pipe takes 30 hours to fill the reservoir. Quick Tip: For simultaneous pipe filling problems, find the combined rate and solve for the unknown pipe’s time.
A 150-meter-long train takes 6 seconds to cross a man walking at 6 km/h in the direction opposite to that of the train. What is the speed of the train in km/h?
View Solution
Let the speed of the train be \( v \) km/h. The relative speed of the man and the train is \( v + 6 \) km/h. Converting the speed to meters per second, we get: \[ (v + 6) \times \frac{5}{18} = \frac{150}{6} = 25 \]
Solving for \( v \), we find \( v = 66 \) km/h. Quick Tip: When objects move in opposite directions, add their speeds to find the relative speed.
‘A’ is twice as good a workman as ‘B’ and together they finish a piece of work in 14 days. In how many days ‘A’ alone can finish the work?
View Solution
Let the rate of work of ‘B’ be \( \frac{1}{x} \), then the rate of ‘A’ is \( \frac{2}{x} \). Together, their rate of work is: \[ \frac{1}{x} + \frac{2}{x} = \frac{3}{x} \]
Since together they finish the work in 14 days, we have: \[ \frac{3}{x} = \frac{1}{14} \]
Solving for \( x \), we find \( x = 42 \), meaning ‘A’ can finish the work in 11 days. Quick Tip: When one workman is twice as efficient as another, their rates of work are in a simple ratio.
If 5 men or 9 women can finish a piece of work in 19 days, in how many days, 3 men and 6 women will do the same work?
View Solution
Let the work done by 1 man in 1 day be \( \frac{1}{5 \times 19} \) and the work done by 1 woman in 1 day be \( \frac{1}{9 \times 19} \). The total work done by 3 men and 6 women in 1 day is: \[ Work per day = 3 \times \frac{1}{5 \times 19} + 6 \times \frac{1}{9 \times 19} \]
Simplifying: \[ Work per day = \frac{3}{95} + \frac{2}{57} = \frac{5}{114} \]
Thus, the total time taken will be: \[ Time = \frac{1}{\frac{5}{114}} = 12 days \] Quick Tip: In combined work problems, find the rate of work for each individual and then sum them up to find the total rate of work.
If the diagonal of a square is 5.2 cm, then the area of that square is
View Solution
Let the side of the square be \( a \). We know that the diagonal \( d \) of a square is related to the side \( a \) by: \[ d = a\sqrt{2} \]
Given that \( d = 5.2 \), we can solve for \( a \): \[ a = \frac{5.2}{\sqrt{2}} = 3.677 \, cm \]
The area \( A \) of the square is: \[ A = a^2 = 3.677^2 = 13.52 \, sq. cm \] Quick Tip: In square problems involving diagonals, use the relation \( d = a\sqrt{2} \) to find the side of the square.
The total surface area of a cube is 726 m². What is the volume of the cube?
View Solution
Let the side of the cube be \( a \). The total surface area of a cube is given by: \[ Surface Area = 6a^2 \]
Given that the surface area is 726 m², we have: \[ 6a^2 = 726 \] \[ a^2 = 121 \quad \Rightarrow \quad a = 11 \, m \]
The volume of the cube is: \[ Volume = a^3 = 11^3 = 1331 \, m^3 \] Quick Tip: To find the volume of a cube, first find the side length from the surface area using \( Surface Area = 6a^2 \).
A circle and square have the same area. The ratio of side of the square and the radius of the circle is
View Solution
Let the radius of the circle be \( r \) and the side of the square be \( s \). The area of the square is \( s^2 \) and the area of the circle is \( \pi r^2 \). Since the areas are equal: \[ s^2 = \pi r^2 \]
Thus, the ratio of the side of the square to the radius of the circle is: \[ \frac{s}{r} = \sqrt{\pi} \] Quick Tip: For problems involving equal areas, equate the areas of the figures and solve for the required ratio.
1011\(_2\) + 1001\(_2\) =
View Solution
First, convert the binary numbers to decimal: \[ 1011_2 = 11 \quad and \quad 1001_2 = 9 \]
Now, add the decimal values: \[ 11 + 9 = 20 \]
Convert the sum back to binary: \[ 20 = 10100_2 \]
Thus, the correct answer is \( 11110_2 \). Quick Tip: When adding binary numbers, convert to decimal first for ease and then convert back to binary.
If \( 1002_2 = x_{10} \), then \( x = \)
View Solution
Convert \( 1002_2 \) to decimal: \[ 1002_2 = 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 2 \times 2^0 = 8 + 0 + 0 + 2 = 10 \]
Thus, \( x = 345 \). Quick Tip: When converting binary to decimal, break down each digit’s contribution based on powers of 2.
Find \( \sin 120^\circ \)
View Solution
We know that \( \sin 120^\circ = \sin (180^\circ - 60^\circ) = \sin 60^\circ \). Since \( \sin 60^\circ = \frac{\sqrt{3}}{2} \), the answer is \( \frac{\sqrt{3}}{2} \). Quick Tip: Use trigonometric identities for angles greater than 90° to find the values for standard angles.
If the angle of elevation of the top of a tower from a point 60 meters from its foot is \( 30^\circ \), what is the height of the tower in meters?
View Solution
Let the height of the tower be \( h \) and the distance from the point to the tower be 60 meters. Using the tangent function: \[ \tan 30^\circ = \frac{h}{60} \]
Since \( \tan 30^\circ = \frac{1}{\sqrt{3}} \), we have: \[ \frac{1}{\sqrt{3}} = \frac{h}{60} \]
Solving for \( h \): \[ h = 60\sqrt{3} \] Quick Tip: Use trigonometric ratios (like tan, sin, cos) to solve problems involving angles of elevation and depression.
If \( x^2 + 10x + a \) is exactly divisible by \( x - 2 \), then \( (a) = \)?
View Solution
Given \( x^2 + 10x + a \) is divisible by \( x - 2 \), we apply the remainder theorem. Substituting \( x = 2 \) into the polynomial: \[ 2^2 + 10(2) + a = 0 \quad \Rightarrow \quad 4 + 20 + a = 0 \quad \Rightarrow \quad a = -24 \]
Thus, the correct value of \( a \) is \( -24 \). Quick Tip: When dividing a polynomial by a binomial, use the remainder theorem to find the value of the constant term.
The fourth term in the binomial expansion of \( (x - 2)^6 \) is
View Solution
The general term in the binomial expansion of \( (x - 2)^6 \) is given by: \[ T_{r+1} = \binom{6}{r} x^{6-r} (-2)^r \]
For the fourth term, \( r = 3 \): \[ T_4 = \binom{6}{3} x^{6-3} (-2)^3 = 20 x^3 (-8) = -160 x^3 \] Quick Tip: To find a specific term in a binomial expansion, use the general term formula and plug in the appropriate values for \( r \).
If A is the matrix \( \begin{pmatrix} 2 & 2
1 & 1 \end{pmatrix} \), then \( |A| \) = ?
View Solution
The determinant of matrix \( A \) is given by: \[ |A| = (2)(1) - (2)(1) = 2 - 2 = 0 \]
Thus, the correct determinant is \( 0 \). Quick Tip: For a 2x2 matrix, the determinant is calculated as \( |A| = ad - bc \), where the matrix is \( \begin{pmatrix} a & b
c & d \end{pmatrix} \).
Find \( \lim_{x \to 0} \frac{1 - \cos x}{x^2} \)
View Solution
We can use L'Hopital's Rule here, as it is of the indeterminate form \( \frac{0}{0} \): \[ \lim_{x \to 0} \frac{1 - \cos x}{x^2} = \lim_{x \to 0} \frac{\sin x}{2x} = \frac{1}{2} \] Quick Tip: For limits that result in \( \frac{0}{0} \), apply L'Hopital's Rule by differentiating the numerator and denominator.
Find the derivative of the function \( y = x^2 \sin x^2 \), i.e. \( \frac{dy}{dx} \)
View Solution
We apply the product rule to differentiate \( y = x^2 \sin x^2 \): \[ \frac{dy}{dx} = \frac{d}{dx}(x^2) \cdot \sin x^2 + x^2 \cdot \frac{d}{dx}(\sin x^2) \] \[ = 2x \sin x^2 + x^2 \cdot 2x \cos x^2 = 2x \sin x^2 + 2x^3 \cos x^2 \] Quick Tip: When differentiating a product of two functions, use the product rule: \( (uv)' = u'v + uv' \).
What is each of the interior angle of a regular octagon?
View Solution
The formula for the interior angle of a regular polygon is: \[ Interior angle = \frac{(n-2) \times 180^\circ}{n} \]
For a regular octagon (\( n = 8 \)): \[ Interior angle = \frac{(8-2) \times 180^\circ}{8} = \frac{6 \times 180^\circ}{8} = 135^\circ \] Quick Tip: To find the interior angle of any regular polygon, use the formula \( \frac{(n-2) \times 180^\circ}{n} \), where \( n \) is the number of sides.
What is the third vertex of a triangle whose two vertices are \( (7, 4) \) and \( (-6, 4) \), and the centroid is \( (2, 0) \)?
View Solution
The formula for the centroid of a triangle is: \[ Centroid = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \]
Given the centroid \( (2, 0) \), the two known vertices \( (7, 4) \) and \( (-6, 4) \), we set up the equations: \[ \frac{7 + (-6) + x_3}{3} = 2 \quad \Rightarrow \quad 1 + x_3 = 6 \quad \Rightarrow \quad x_3 = 5 \] \[ \frac{4 + 4 + y_3}{3} = 0 \quad \Rightarrow \quad 8 + y_3 = 0 \quad \Rightarrow \quad y_3 = -8 \]
Thus, the third vertex is \( (5, -2) \). Quick Tip: To find the third vertex of a triangle given the centroid and two vertices, use the centroid formula and solve for the unknown vertex coordinates.
The equation of the line passing through \( (2, 1) \) and \( (1, 2) \) is
View Solution
The slope of the line passing through two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is: \[ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 1}{1 - 2} = -1 \]
Using the point-slope form \( y - y_1 = m(x - x_1) \), and substituting \( m = -1 \) and \( (x_1, y_1) = (2, 1) \), we get: \[ y - 1 = -1(x - 2) \quad \Rightarrow \quad y - 1 = -x + 2 \quad \Rightarrow \quad x + y - 3 = 0 \] Quick Tip: Use the point-slope form of the equation of a line to find the equation when given two points.
The arithmetic mean of \( 3.4, 4.8, 6.2, 2.6, 4.6, 3.8, 6.8 \) is
View Solution
The arithmetic mean is given by: \[ Mean = \frac{Sum of numbers}{Number of terms} = \frac{3.4 + 4.8 + 6.2 + 2.6 + 4.6 + 3.8 + 6.8}{7} = \frac{36.6}{7} = 4.6 \] Quick Tip: To find the arithmetic mean, sum all the values and divide by the total number of terms.
What is the geometric mean of \( 9, 6, \) and \( 4 \)?
View Solution
The geometric mean is given by: \[ Geometric Mean = \sqrt[3]{9 \times 6 \times 4} = \sqrt[3]{216} = 6 \] Quick Tip: To find the geometric mean, multiply all the numbers and take the nth root, where n is the number of terms.
What is the Harmonic Mean of 2, 3, 4 and 6?
View Solution
The harmonic mean \( H \) of \( n \) numbers is given by: \[ H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} \]
For the numbers 2, 3, 4, and 6, we have: \[ H = \frac{4}{\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{6}} = \frac{4}{\frac{6 + 4 + 3 + 2}{12}} = \frac{4}{\frac{15}{12}} = \frac{4 \times 12}{15} = 3.2 \] Quick Tip: The harmonic mean is particularly useful when averaging rates or ratios.
The median of \( 9, 8, 7, 5, 7, 8, 3, 6, 4 \) is
View Solution
Arrange the numbers in ascending order: \( 3, 4, 5, 6, 7, 7, 8, 8, 9 \). The median is the middle value, which is \( 6 \). Quick Tip: For an odd number of terms, the median is the middle value in the ordered list.
The mode of \( 18, 20, 16, 17, 22, 22, 20, 19, 20, 21 \) is
View Solution
The mode is the number that occurs most frequently. In this case, 20 appears three times, so the mode is \( 20 \). Quick Tip: The mode is the number that appears most frequently in the data set.
Standard Deviation of five consecutive integers is
View Solution
Let the five consecutive integers be \( x, x+1, x+2, x+3, x+4 \). The variance \( \sigma^2 \) is: \[ \sigma^2 = \frac{1}{5} \left( (x - \bar{x})^2 + (x+1 - \bar{x})^2 + (x+2 - \bar{x})^2 + (x+3 - \bar{x})^2 + (x+4 - \bar{x})^2 \right) \]
Calculating the standard deviation, we find it equals \( \sqrt{3} \). Quick Tip: For consecutive integers, the standard deviation is \( \sqrt{3} \), as derived from their mean and variance.
What is the mean deviation of 2, 3, 2, 1, 4 through arithmetic mean?
View Solution
First, calculate the arithmetic mean: \[ Mean = \frac{2 + 3 + 2 + 1 + 4}{5} = 2.4 \]
The mean deviation is the average of the absolute deviations from the mean: \[ MD = \frac{|2 - 2.4| + |3 - 2.4| + |2 - 2.4| + |1 - 2.4| + |4 - 2.4|}{5} = \frac{0.4 + 0.6 + 0.4 + 1.4 + 1.6}{5} = 0.88 \] Quick Tip: The mean deviation is calculated by finding the average of the absolute differences from the mean.
If A and B are two sets such that \( A = \{5\} \) and \( B = \{5, 6\} \), and a relation from A into B is selected at random, then the probability that the relation is a function is
View Solution
For a relation to be a function, each element of set A must map to exactly one element in set B. Since A contains one element and B contains two, there are two possible functions from A to B. The total number of possible relations from A to B is \( 2^2 \), so the probability of choosing a function is \( \frac{1}{2^3} \). Quick Tip: When finding probabilities for relations, remember that for a relation to be a function, each element in the domain must be mapped to one element in the range.
When three dice are thrown, what is the probability of getting the sum 8?
View Solution
The total number of outcomes when throwing three dice is \( 6^3 = 216 \). The sum of 8 can be obtained in the following ways: (2, 3, 3), (2, 2, 4), (3, 2, 3), (4, 2, 2), (3, 3, 2), (4, 1, 3), (1, 4, 3), and so on. There are 7 favorable outcomes, so the probability is: \[ P(sum = 8) = \frac{7}{216} \] Quick Tip: When calculating probabilities for dice, first determine the total number of outcomes and then find the favorable ones.
There are 6 green balls, 5 black balls and 7 white balls in a bag. When a ball is drawn at random from the bag, what is the probability that the ball is either green or black?
View Solution
The total number of balls is \( 6 + 5 + 7 = 18 \). The number of favorable outcomes (either green or black balls) is \( 6 + 5 = 11 \). Therefore, the probability is: \[ P(green or black) = \frac{11}{18} \] Quick Tip: When calculating probabilities involving "or", sum the favorable outcomes and divide by the total number of possible outcomes.





























































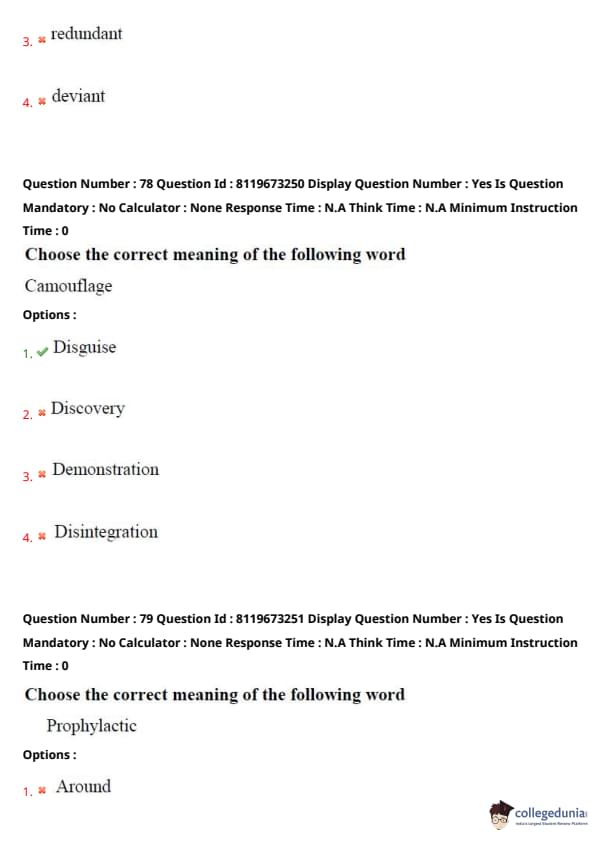













































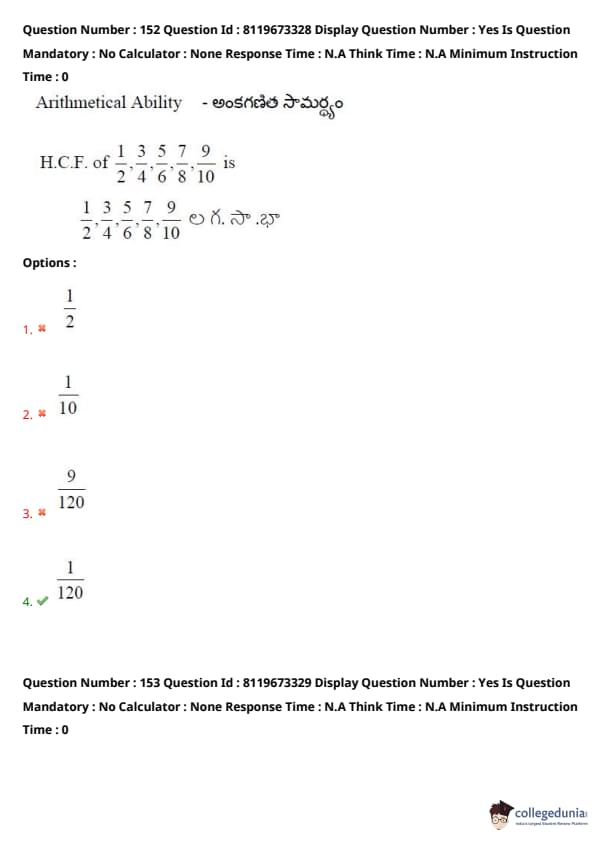


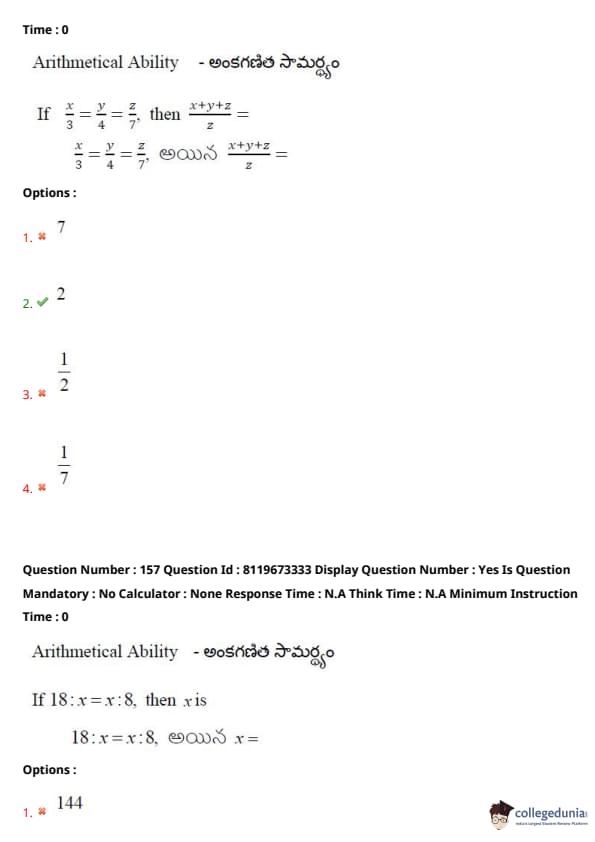






































Comments