APICET 2024 Question Paper with Answer Key pdf is available for download here. Sri Krishnadevaraya University conducted APICET on May 6, 2024 in Shift 1. APICET 2024 question paper consists of total 200 questions carrying a total weightage of 200 marks. Candidates are given 150 minutes to attempt APICET Question Paper.
APICET 2024 Question Paper with Answer Key PDF (May 6 - Shift 1)
| APICET 2024 May 6 Shift 1 Question Paper with Answer Key | Download PDF | Check Solution |

Question 1:
What is the cost of each pen?
I. Cost of 3 pens and 4 pencils is Rs. 10
II. Cost of 12 pencils and 9 pens is Rs. 30
View Solution
Let the cost of a pen be \( p \) and the cost of a pencil be \( q \).
From the first piece of information, we have the equation: \[ 3p + 4q = 10 \]
From the second piece of information, we have the equation: \[ 12q + 9p = 30 \]
Now, solve this system of equations. First, multiply the first equation by 3 and the second equation by 1 to make the coefficients of \( p \) the same: \[ 9p + 12q = 30 \]
Subtract the first equation from the second: \[ (9p + 12q) - (3p + 4q) = 30 - 10 \] \[ 6p + 8q - 4q = 20 \] \[ 6p + 4q = 20 \]
Now, divide through by 2: \[ 3p + 2q = 10 \]
Next, subtract this equation from the first one: \[ (3p + 4q) - (3p + 2q) = 10 - 10 \] \[ 2q = 0 \] \[ q = 0 \]
Now substitute \( q = 0 \) into the first equation: \[ 3p + 4(0) = 10 \] \[ 3p = 10 \] \[ p = \frac{10}{3} \approx 3.33 \]
Thus, the cost of each pen is approximately Rs. 3.33. Since the answer closest to this is option 4, the correct answer is \( \boxed{4} \). Quick Tip: When solving word problems involving the cost of items, form equations based on the given conditions and solve the system of equations to find the unknown values.
What is the value of \( X \)?
I. \( X + 3Y = 9 \)
II. \( 3X + 9Y = 27 \)
View Solution
From the first equation: \[ X + 3Y = 9 \]
From the second equation: \[ 3X + 9Y = 27 \]
Notice that the second equation is simply three times the first equation: \[ 3(X + 3Y) = 27 \] \[ 3 \times 9 = 27 \]
This is true, so the two equations are consistent and provide the same information. Therefore, we can solve for \( X \) using the first equation: \[ X + 3Y = 9 \]
Solving for \( X \) in terms of \( Y \): \[ X = 9 - 3Y \]
Thus, the value of \( X \) depends on \( Y \), and there is no unique solution for \( X \) without knowing the value of \( Y \). Since this doesn't provide enough information to determine a specific numerical value for \( X \), the correct answer is \( \boxed{4} \). Quick Tip: When solving systems of linear equations, ensure the equations are consistent and check if one is a multiple of the other to avoid redundant equations.
For the positive integer \( n \), is \( n - 10 \) odd?
I. \( n - 16 \) is a positive integer
II. \( n + 12 \) is even
View Solution
We are asked if \( n - 10 \) is odd. To answer this, we need to use the given conditions.
From the first condition, \( n - 16 \) is a positive integer.
This means that: \[ n - 16 > 0 \quad \Rightarrow \quad n > 16 \]
So, \( n \) must be greater than 16.
From the second condition, \( n + 12 \) is even.
For \( n + 12 \) to be even, \( n \) itself must be even, because an even number added to 12 (an even number) results in an even number.
Thus, \( n \) is even.
Now, we know that \( n \) is an even integer greater than 16. We need to check if \( n - 10 \) is odd.
Since \( n \) is even, we have: \[ n - 10 = even number - 10 = even number \]
Thus, \( n - 10 \) is even, not odd. Therefore, the answer is "No, \( n - 10 \) is not odd."
Thus, the correct answer is \( \boxed{2} \). Quick Tip: When checking if an expression is odd or even, remember that:
- An even number minus an even number is even.
- An odd number minus an odd number is even.
- An even number minus an odd number is odd.
Four friends, A, B, C, and D got the top four ranks in a test but A did not get the first, B did not get the second, C did not get the third, and D did not get the fourth. Who secured which rank?
I. Neither A nor D were among the first 2 ranks.
II. Neither B nor C was third or fourth.
View Solution
From the given conditions:
- A did not get the first, so A can only be second, third, or fourth.
- B did not get the second, so B can only be first, third, or fourth.
- C did not get the third, so C can only be first, second, or fourth.
- D did not get the fourth, so D can only be first, second, or third.
Now, let's use the information from the clues:
- From condition I: Neither A nor D were among the first two ranks. Therefore, A and D must be in third and fourth ranks, and B and C must be first and second.
- From condition II: Neither B nor C was third or fourth, meaning B and C must occupy the first and second ranks. Since A cannot be first, A must be second. Therefore, B must be first and C must be second.
Thus, the ranks are:
- B secured the first rank.
- C secured the second rank.
- A secured the third rank.
- D secured the fourth rank.
The correct answer is \( \boxed{3} \). Quick Tip: When solving rank-based logic puzzles, use the process of elimination to narrow down the possibilities based on the given constraints.
What is the value of \( x \) in the equation \( 2x + 5 = 11 \)?
I. \( x = 3 \)
II. \( x \) is a prime number.
View Solution
We are given the equation: \[ 2x + 5 = 11 \]
First, subtract 5 from both sides of the equation: \[ 2x = 11 - 5 \] \[ 2x = 6 \]
Now, divide both sides by 2: \[ x = \frac{6}{2} = 3 \]
Thus, the value of \( x \) is 3, which satisfies both conditions:
- \( x = 3 \) (Condition I),
- 3 is a prime number (Condition II).
Thus, the correct answer is \( \boxed{1} \). Quick Tip: When solving linear equations, always isolate the variable by performing operations on both sides of the equation.
What is the two-digit number whose first digit is \( a \) and the second digit is \( b \)?
I. The number is a multiple of 62.
II. \( a + b = 9 \).
View Solution
Let the two-digit number be \( 10a + b \), where \( a \) is the tens digit and \( b \) is the ones digit.
From condition I: The number is a multiple of 62, so we check the multiples of 62 within the two-digit range: \[ 62 \times 1 = 62 \quad (valid two-digit number) \] \[ 62 \times 2 = 124 \quad (not a valid two-digit number) \]
So, the number must be 62.
From condition II: \( a + b = 9 \), where \( a = 6 \) and \( b = 2 \). Thus, \( 6 + 2 = 9 \), which satisfies the condition.
Therefore, the two-digit number is \( 62 \).
Thus, the correct answer is \( \boxed{1} \). Quick Tip: When solving for a specific number, use the given conditions to check possible values that satisfy both the mathematical conditions and logical constraints.
What is the cost of the book?
I. A man earns a profit of 25% on selling a book.
II. The selling price of the book is Rs. 5000.
View Solution
Let the cost price of the book be \( C \) rupees.
The man earns a profit of 25% on the cost price.
This means the selling price is \( 125% \) of the cost price, or: \[ Selling Price = 1.25 \times C \]
We are given that the selling price of the book is Rs. 5000. Therefore: \[ 1.25 \times C = 5000 \]
Solving for \( C \): \[ C = \frac{5000}{1.25} = 4000 \]
Thus, the cost price of the book is Rs. 4000.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When calculating the cost price using a profit percentage, remember that the selling price is the cost price plus the profit percentage of the cost price.
What is Priya's rank from the top in a class of seventy students?
I. There are six students between Priya and Charan.
II. Charan is eight from the top.
View Solution
Let us assume Priya's rank from the top is \( P \) and Charan's rank from the top is \( C \).
We are given that there are six students between Priya and Charan, which means the difference in their ranks is 7. Hence, we can write: \[ |P - C| = 7 \]
From condition II, Charan's rank is 8th from the top: \[ C = 8 \]
Now, using the equation \( |P - 8| = 7 \), we can solve for Priya's rank \( P \): \[ P - 8 = 7 \quad or \quad 8 - P = 7 \]
Solving the first equation: \[ P = 15 \]
Solving the second equation: \[ P = 1 \]
So, Priya can either be 1st or 15th. Since there are 70 students in the class, Priya's rank from the top is the 15th position.
Thus, Priya's rank is \( \boxed{15} \). Quick Tip: In ranking problems, carefully analyze the conditions about the positions of the individuals to calculate their exact ranks using simple algebraic expressions.
What % of 32 is \( x \)?
I. \( x \) is 10 percent of 20.
II. 800% of \( x \) is less than 4.
View Solution
From condition I, \( x \) is 10 percent of 20: \[ x = \frac{10}{100} \times 20 = 2 \]
So, \( x = 2 \).
Now, we substitute \( x = 2 \) in the original equation to find what percentage of 32 is \( x \): \[ \frac{x}{32} \times 100 = \frac{2}{32} \times 100 = \frac{200}{32} = 6.25% \]
Thus, \( x \) is 6.25% of 32.
Therefore, the correct answer is \( \boxed{1} \). Quick Tip: When calculating percentages, multiply by the percentage (in decimal form) and use simple algebra to solve for the unknown variable.
How is Deepa related to Laxmi?
I. Deepa’s mother is the sister of Laxmi’s father.
II. Deepa is the daughter of Laxmi’s grandfather’s only son.
View Solution
Let us analyze the given information:
- From condition I: Deepa’s mother is the sister of Laxmi’s father. This means Deepa’s mother and Laxmi’s father are siblings. Therefore, Deepa’s mother is Laxmi’s aunt.
- From condition II: Deepa is the daughter of Laxmi’s grandfather’s only son. This means Deepa’s father is Laxmi’s uncle.
So, Deepa is the niece of Laxmi.
Thus, the correct answer is \( \boxed{1} \). Quick Tip: When dealing with family relationship questions, start by identifying the relationships step-by-step, and determine the exact position of the individuals in the family tree.
What is the present age of Shilpa?
I. Shilpa's present age is five times of Rahul's present age.
II. Five years ago her age was twenty-five times of Rahul's age at that time.
View Solution
Let Shilpa's present age be \( S \) and Rahul's present age be \( R \).
From condition I: \[ S = 5R \]
From condition II: Five years ago, Shilpa's age was 25 times Rahul's age at that time.
So, five years ago, Shilpa’s age was \( S - 5 \) and Rahul’s age was \( R - 5 \).
The equation becomes: \[ S - 5 = 25(R - 5) \]
Substitute \( S = 5R \) into this equation: \[ 5R - 5 = 25(R - 5) \]
Simplifying: \[ 5R - 5 = 25R - 125 \] \[ 5R - 25R = -125 + 5 \] \[ -20R = -120 \] \[ R = 6 \]
Now substitute \( R = 6 \) into \( S = 5R \): \[ S = 5 \times 6 = 30 \]
Thus, Shilpa’s present age is \( \boxed{30} \).
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When dealing with age-related problems, set up algebraic equations based on the given relationships and solve for the unknowns systematically.
How is PROCESS written in that code language?
I. In a certain code language, QUEUE is written as RVFVF.
II. In a certain code language, CRWTH is written as BQVSG.
View Solution
We are given two examples of how words are coded in a certain code language. Let’s analyze the pattern in each case.
- In the first example:
QUEUE is written as RVFVF.
Look at how each letter changes:
\[ Q \rightarrow R, \, U \rightarrow V, \, E \rightarrow F, \, E \rightarrow V, \, U \rightarrow F \]
Each letter is shifted by a certain value. Specifically, each letter is shifted forward by 1 position in the alphabet, except for the 3rd and 5th letters, which are shifted by 1 and 3 positions respectively.
- In the second example:
CRWTH is written as BQVSG.
Let’s analyze the pattern of the shifts for each letter:
\[ C \rightarrow B, \, R \rightarrow Q, \, W \rightarrow V, \, T \rightarrow S, \, H \rightarrow G \]
Each letter is shifted backwards by 1 position.
By applying the same pattern to the word PROCESS:
- \( P \rightarrow O \) (shifted back by 1),
- \( R \rightarrow Q \) (shifted back by 1),
- \( O \rightarrow N \) (shifted back by 1),
- \( C \rightarrow B \) (shifted back by 1),
- \( E \rightarrow D \) (shifted back by 1),
- \( S \rightarrow R \) (shifted back by 1).
Thus, PROCESS is written as **OQNBDR** in the code language.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When solving coding and pattern problems, carefully analyze how each letter of the word changes and identify the shifts or operations applied to the letters.
Is the integer number \( n \) divisible by 15?
I. 9 divides \( n \).
II. 20 divides \( n \).
View Solution
We are asked whether the integer number \( n \) is divisible by 15. To determine this, we need to check if \( n \) satisfies the divisibility rule for 15.
- From condition I: 9 divides \( n \), meaning \( n \) is divisible by 9.
- From condition II: 20 divides \( n \), meaning \( n \) is divisible by 20.
Since 15 is the product of 3 and 5, for \( n \) to be divisible by 15, it must also be divisible by both 3 and 5. We are given that \( n \) is divisible by 9 and 20:
- Divisibility by 9 already guarantees divisibility by 3, since 9 is a multiple of 3.
- Divisibility by 20 guarantees divisibility by 5, since 20 is a multiple of 5.
Thus, since \( n \) is divisible by both 9 and 20, it is also divisible by 15.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When checking divisibility for composite numbers, ensure that \( n \) is divisible by the prime factors of that number. In this case, check divisibility by 3 and 5 to determine divisibility by 15.
How many pages of book X did Robert read on Sunday?
I. The book has 300 pages out of which two-thirds were read by him before Sunday.
II. Robert read the last 40 pages of the book on the morning of Monday.
View Solution
Let the total number of pages in the book be 300.
- From condition I, two-thirds of the book was read by Robert before Sunday. Therefore, the number of pages read by him before Sunday is:
\[ \frac{2}{3} \times 300 = 200 \, pages \]
- From condition II, Robert read the last 40 pages on Monday. This means that the number of pages Robert read on Sunday is the remainder of the book after subtracting the 200 pages read before Sunday and the 40 pages read on Monday:
\[ 300 - 200 - 40 = 60 \, pages \]
Thus, Robert read 60 pages on Sunday.
Therefore, the correct answer is \( \boxed{3} \).
Quick Tip: When solving problems involving fractions of a total, break the problem into manageable steps. First calculate the known quantities and then subtract from the total to find the unknown.
How many employees of the Bank opted for VRS?
I. 22% of the 950 officer cadre employees and 16% of the 1100 other cadre employees opted for VRS.
II. 32% of the employees in the age group of 53 to 59 and 19% of the employees in all other age groups opted for VRS.
View Solution
Let’s calculate the number of employees who opted for VRS based on the given information.
- From condition I:
- Number of officer cadre employees = 950.
- 22% of these employees opted for VRS:
\[ \frac{22}{100} \times 950 = 209 \, employees \]
- Number of other cadre employees = 1100.
- 16% of these employees opted for VRS:
\[ \frac{16}{100} \times 1100 = 176 \, employees \]
- Total number of employees who opted for VRS (from condition I) is:
\[ 209 + 176 = 385 \, employees \]
Thus, from condition I, 385 employees opted for VRS.
- From condition II:
- 32\ of employees in the age group of 53 to 59 opted for VRS.
- 19% of employees in all other age groups opted for VRS.
However, since we don't have the exact number of employees in each age group, we cannot calculate the total number of employees based on condition II alone.
Therefore, we conclude that the total number of employees who opted for VRS based on the information given in condition I is \( \boxed{385} \).
Thus, the correct answer is \( \boxed{1} \). Quick Tip: When dealing with percentage-based problems, calculate the percentage of each group separately and then add them together for the total.
What is the total distance travelled by a train?
I. The train travelled at an average speed of 80 km/h for 4 hours.
II. The train travelled at an average speed of 100 km/h for 2 hours.
View Solution
We are asked to calculate the total distance travelled by the train. The distance travelled by a train is given by the formula:
\[ Distance = Speed \times Time \]
- From condition I:
The train travelled at an average speed of 80 km/h for 4 hours. The distance covered in this time is:
\[ Distance_1 = 80 \, km/h \times 4 \, hours = 320 \, km \]
- From condition II:
The train travelled at an average speed of 100 km/h for 2 hours. The distance covered in this time is:
\[ Distance_2 = 100 \, km/h \times 2 \, hours = 200 \, km \]
Thus, the total distance travelled by the train is: \[ Total Distance = 320 \, km + 200 \, km = 520 \, km \]
Therefore, the total distance travelled by the train is \( \boxed{520} \, km \).
Thus, the correct answer is \( \boxed{4} \). Quick Tip: To calculate the total distance, use the formula \( Distance = Speed \times Time \), and add the distances covered in each segment.
How many persons attended the meeting?
I. Each registered person can take two persons with him/her.
II. There were totally 180 registrations for the meeting.
View Solution
Let the number of registered persons be \( x \). According to the problem, each registered person can take 2 persons with him/her, meaning the total number of persons who attended the meeting is: \[ Total persons = x + 2x = 3x \]
From condition II, the total number of registrations is 180. Since each registration represents one person, we have: \[ x = 180 \]
Thus, the total number of persons who attended the meeting is: \[ 3x = 3 \times 180 = 540 \]
Therefore, the correct answer is \( \boxed{540} \).
Thus, the correct answer is \( \boxed{4} \). Quick Tip: When given conditions with multipliers or groups, express the total number in terms of the variables and solve accordingly.
In the two triangles, what is the value of \( P + Q + R + S \)?
I. \( A + B = 90^\circ \)
II. \( P + Q = R + S \)
View Solution
We are given two triangles with angles \( P, Q, R, S \), and other conditions.
- From condition I: \( A + B = 90^\circ \), this means the angles \( A \) and \( B \) in the first triangle add up to 90 degrees. This implies that the remaining two angles in the first triangle must also add up to 90 degrees.
- From condition II: \( P + Q = R + S \), this equation means that the sum of angles \( P \) and \( Q \) is equal to the sum of angles \( R \) and \( S \).
In any triangle, the sum of the interior angles is always \( 180^\circ \). Therefore, in each triangle, the sum of the angles must be \( 180^\circ \). Thus: \[ P + Q + R + S = 180^\circ + 180^\circ = 360^\circ \]
Therefore, the value of \( P + Q + R + S \) is \( 360^\circ \).
Thus, the correct answer is \( \boxed{1} \). Quick Tip: In geometric problems involving triangles, remember that the sum of the angles in any triangle is always 180 degrees.
What is the age difference between Peter and his brother?
I. Peter's age is 3 times his brother's age.
II. The sum of Peter's and his brother's age is 40 years.
View Solution
Let Peter's age be \( P \) and his brother's age be \( B \).
From condition I: Peter's age is 3 times his brother's age.
This gives the equation: \[ P = 3B \]
From condition II: The sum of their ages is 40 years. \[ P + B = 40 \]
Now, substitute \( P = 3B \) into the second equation: \[ 3B + B = 40 \] \[ 4B = 40 \] \[ B = 10 \]
Now that we know the brother’s age is 10 years, substitute this back into \( P = 3B \) to find Peter's age: \[ P = 3 \times 10 = 30 \]
The age difference between Peter and his brother is: \[ P - B = 30 - 10 = 20 \]
Thus, the age difference between Peter and his brother is \( \boxed{20} \) years.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When solving age-related problems, create variables for the unknowns and use the given conditions to form equations that can be solved algebraically.
How many students scored more than the average marks of the class in a test?
I. The average marks of the class was 70.
II. 10 students scored above the arithmetic mean of the class.
View Solution
Let the total number of students in the class be \( n \).
- From condition I, the average marks of the class were 70. This means the total marks of the class, denoted by \( T \), is: \[ T = 70 \times n \]
- From condition II, 10 students scored above the arithmetic mean (average) of the class. This means there are 10 students whose scores are greater than 70.
Since the total number of students who scored above the average is 10, and no other information is provided, we can conclude that the number of students who scored more than the average is 10.
Thus, the correct answer is \( \boxed{2} \). Quick Tip: In problems related to averages and percentages, be sure to differentiate between the total and the group-specific conditions, such as those above or below the mean.
Find the odd thing from the following:
View Solution
In this case, the odd one out is Chess because:
- Cricket, Hockey, and Football are all physically played sports that involve a ball.
- Chess, on the other hand, is a board game and does not involve a ball.
Thus, Chess is the odd one out.
Therefore, the correct answer is \( \boxed{2} \). Quick Tip: When identifying the odd one out, consider the category or common features shared by most of the items. Look for the one that doesn't belong based on characteristics like physical activity, objects used, or categories.
Find the odd thing from the following:
View Solution
Let’s analyze the patterns for each option:
- In options 1, 2, and 3:
- The first two letters are repeated, e.g., "bb", "cc", "aa".
- The next set of letters follows an alphabetical sequence, and the last letter in each group is one step after the preceding letter in the alphabet.
- In option 4:
- The first two letters are not repeated, "ff" is the only option where the first pair of letters are not the same. Also, "H" and "I" are skipped, and the next letter in the sequence, "L", follows in a different pattern.
Thus, ff Hij L is the odd one out.
Therefore, the correct answer is \( \boxed{4} \). Quick Tip: When identifying the odd one out, look for patterns in the sequences, such as repeated elements, alphabetical order, or position consistency. If one element breaks the pattern, it’s the odd one out.
Find the odd thing from the following:
View Solution
Let’s analyze the given numbers:
- 121 = \( 11^2 \) (perfect square)
- 144 = \( 12^2 \) (perfect square)
- 169 = \( 13^2 \) (perfect square)
- 226 is not a perfect square.
The first three numbers are perfect squares, but 226 is not. Therefore, 226 is the odd one out.
Thus, the correct answer is \( \boxed{4} \). Quick Tip: To identify the odd one out, look for a pattern or common property among the items, such as being a perfect square, prime number, or multiple of a specific number.
Find the odd thing from the following:
View Solution
Let’s analyze the terms:
- Nephrology is the study of kidneys.
- Astrology is the study of stars and planets (it is not a medical science).
- Pathology is the study of diseases.
- Mycology is the study of fungi.
Among these, Astrology is different because it is not a medical science, unlike the other fields (Nephrology, Pathology, and Mycology), which are branches of biology or medicine.
Thus, Astrologyis the odd one out.
Therefore, the correct answer is \( \boxed{2} \). Quick Tip: When identifying the odd one out, look for the category or field to which each item belongs. If most items belong to one category and one does not, that is the odd one out.
Find the odd thing from the following:
View Solution
Let's analyze the options:
- Oxygen, Nitrogen, and Carbon are all gaseous elements in the periodic table and are essential for life in various forms.
- Helium, while a gas, is inert and does not play a biological role like the others.
Thus, Helium is the odd one out as it does not participate in life-supporting processes like Oxygen, Nitrogen, and Carbon.
Therefore, the correct answer is \( \boxed{4} \). Quick Tip: When identifying the odd one out, consider the characteristics of each item, such as whether they share a common property or role.
Problem Solving \hspace{2cm Sequence and series \hspace{2cm Odd thing Out
Find the odd thing from the following:
View Solution
Let's analyze the options:
- Sanskrit is a language.
- Ashu Lipi, Sanket Lipi, and Shorthand are all types of scripts or writing systems used for writing languages.
Therefore, Sanskrit is the odd one out as it is a language, while the other options are related to scripts or writing systems.
Thus, the correct answer is \( \boxed{1} \). Quick Tip: When identifying the odd one out, look for the items that belong to different categories. In this case, language vs. script.
Find the odd thing from the following:
View Solution
Let's analyze the options:
- In options 1, 2, and 4, the first two letters in each set follow a simple alphabetical sequence with a pattern of alternating capital and lowercase letters (e.g., "aB", "bC", "tU").
- However, in option 3 ("pQ TU yz"), the first two letters "pQ" are in lowercase, and the next letters are "TU", which are both uppercase, creating a break in the pattern.
Thus, pQ TU yz is the odd one out.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When identifying the odd one out, look for patterns or consistency in formatting or alphabetical sequences.
Find the odd thing from the following:
View Solution
Let's analyze the options:
- Land, Labour, and Capital are all factors of production in economics. These are the inputs needed for the creation of goods and services.
- Profit is the result or outcome of using land, labour, and capital in production, rather than an input.
Thus, Profit is the odd one out.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When identifying the odd one out, look for the category each item belongs to. In this case, factors of production are being compared to the outcome (profit).
Find the odd thing from the following:
View Solution
Let's analyze the given options:
- Apple, Orange, and Pineapple are all fruits that grow on trees.
- Tomato, while botanically a fruit, is often categorized as a vegetable due to its culinary use.
Thus, Tomato is the odd one out because, unlike the others, it is commonly treated as a vegetable.
Therefore, the correct answer is \( \boxed{4} \). Quick Tip: When identifying the odd one out, pay attention to categories such as botanical classification versus culinary usage, as these can often differentiate similar items.
Find the odd thing from the following:
View Solution
Let's analyze the options:
- Nest, Stable, and Hole are all places or structures related to specific animals.
- Nest is a place where birds live.
- Stable is a place where horses are kept.
- Hole refers to a structure often associated with animals like rabbits or moles.
- Boat, on the other hand, is a man-made object used for transportation on water, not related to any animal-specific habitat.
Thus, Boat is the odd one out.
Therefore, the correct answer is \( \boxed{4} \). Quick Tip: When identifying the odd one out, consider the category each item belongs to, such as habitats or structures related to animals vs. inanimate objects.
Find the missing number:
% Given numbers
0.5, 2, 4.5, 8, 12.5, .........
View Solution
Let’s analyze the pattern in the given numbers:
- From 0.5 to 2, the increment is 1.5.
- From 2 to 4.5, the increment is 2.5.
- From 4.5 to 8, the increment is 3.5.
- From 8 to 12.5, the increment is 4.5.
The pattern for the increments is increasing by 1 each time (1.5, 2.5, 3.5, 4.5...).
So, the next increment should be 5.5:
\[ 12.5 + 5.5 = 18 \]
Thus, the missing number is \( 18 \).
Therefore, the correct answer is \( \boxed{18} \). Quick Tip: When solving number series problems, identify the pattern in the differences between the terms. If the differences follow a consistent pattern, continue the pattern to find the missing number.
Find the missing number:
% Given numbers
5, 10, 17, 26, 37, ...........
View Solution
Let's analyze the differences between the consecutive numbers:
- 10 - 5 = 5
- 17 - 10 = 7
- 26 - 17 = 9
- 37 - 26 = 11
The differences are increasing by 2 each time: 5, 7, 9, 11.
So, the next difference should be 13:
\[ 37 + 13 = 50 \]
Thus, the missing number is \( 50 \).
Therefore, the correct answer is \( \boxed{50} \). Quick Tip: In number series problems, identify the pattern in the differences between consecutive numbers. If the differences follow a consistent pattern, continue the pattern to find the missing number.
Find the Missing letter:
% Given sequence
R, U, X, A, D, .........
View Solution
Let's analyze the pattern:
- First, observe the positions of the letters in the alphabet:
- R = 18th letter
- U = 21st letter
- X = 24th letter
- A = 1st letter
- D = 4th letter
The sequence of positions is: 18, 21, 24, 1, 4.
The difference between the positions is:
- 21 - 18 = 3
- 24 - 21 = 3
- 1 - 24 = -23
- 4 - 1 = 3
So, the pattern follows alternating steps of +3, with one large jump (-23) followed by another +3.
Thus, the next letter would be at the 7th position in the alphabet, which corresponds to the letter G.
Therefore, the missing letter is \( \boxed{G} \). Quick Tip: When solving such sequence problems, observe the numeric values of the letters and the pattern in their differences.
Find the Missing letter:
% Given sequence
aB, bB, cD, dD, .........
View Solution
Let's analyze the pattern in the given sequence:
- The first letter alternates between lowercase and uppercase:
- a, b, c, d, and then the next would be e.
- The second letter follows the pattern: B, B, D, D.
The letter repeats for two terms, then increases by 2 (B → D). The next letter in the pattern is F.
Thus, the missing term is eF.
Therefore, the correct answer is \( \boxed{eF} \). Quick Tip: When solving such sequence problems, observe the alternating patterns and the steps between repeated elements to predict the next term.
Find the Missing Number:
% Given sequence
1, 4, 27, 256, 3125, ..........
View Solution
Let’s analyze the pattern in the sequence:
- 1 = \( 1^1 \)
- 4 = \( 2^2 \)
- 27 = \( 3^3 \)
- 256 = \( 4^4 \)
- 3125 = \( 5^5 \)
Each term is the number raised to the power of itself (i.e., \( n^n \)).
Following the same pattern, the next number should be \( 6^6 \):
\[ 6^6 = 46656 \]
Thus, the missing number is \( \boxed{46656} \).
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: In sequence problems, look for patterns where numbers are raised to certain powers or follow mathematical operations. Identifying the pattern helps in predicting the next number in the sequence.
Find the Missing Number:
% Given sequence
9, 10, 16, 33, 83.5, ..........
View Solution
Let's analyze the pattern in the sequence:
- From 9 to 10, the difference is 1.
- From 10 to 16, the difference is 6.
- From 16 to 33, the difference is 17.
- From 33 to 83.5, the difference is 50.5.
The differences between consecutive numbers follow a pattern:
1, 6, 17, 50.5.
The next difference appears to be 151.5, so: \[ 83.5 + 151.5 = 251.5 \]
Thus, the missing number is \( 251.5 \).
Therefore, the correct answer is \( \boxed{251.5} \). Quick Tip: In sequence problems, check for patterns in the differences between terms, as they may follow a mathematical progression that helps identify the next number.
Find the Missing Number:
% Given sequence
273, 264, 239, ....., 109, -12
View Solution
Let's analyze the pattern in the sequence:
- From 273 to 264, the difference is -9.
- From 264 to 239, the difference is -25.
The differences are increasing:
-9, -25, ...
The next difference should follow the pattern. The difference between -9 and -25 is -16, so the next difference should be -41 (since the differences are increasing by 16 each time).
Thus, from 239: \[ 239 - 41 = 190 \]
Therefore, the missing number is \( \boxed{190} \). Quick Tip: When identifying patterns in number series, observe the changes in the differences between the terms. The next difference often follows a consistent progression.
Find the Missing Number:
% Given sequence
6, 12, 20, 30, 42, ..........
View Solution
Let's analyze the pattern in the sequence:
- From 6 to 12, the difference is 6.
- From 12 to 20, the difference is 8.
- From 20 to 30, the difference is 10.
- From 30 to 42, the difference is 12.
The differences between consecutive numbers are increasing by 2 each time: 6, 8, 10, 12.
Following the same pattern, the next difference should be 14: \[ 42 + 14 = 56 \]
Thus, the missing number is \( \boxed{56} \).
Therefore, the correct answer is \( \boxed{4} \).
Quick Tip: When solving sequence problems, observe the differences between consecutive numbers. If the differences follow a consistent pattern, continue the pattern to find the missing number.
Find the Missing Number:
% Given sequence
32, 40, 24, 16, 24, ........
View Solution
Let's analyze the pattern in the sequence:
- The numbers are alternating between increases and decreases.
- From 32 to 40, the difference is +8.
- From 40 to 24, the difference is -16.
- From 24 to 16, the difference is -8.
- From 16 to 24, the difference is +8.
It follows a pattern of alternating between +8 and -8, with -16 as the only exception.
So, following this pattern, the next difference should be -8: \[ 24 - 8 = 16 \]
Thus, the missing number is \( \boxed{8} \).
Therefore, the correct answer is \( \boxed{3} \).
Quick Tip: Look for alternating patterns and differences between terms when solving number series problems. In some cases, the pattern may repeat with certain numbers changing incrementally.
Find the Missing Number:
% Given sequence
3, 4, 7, 8, 11, 12, .........
View Solution
Let's analyze the pattern in the sequence:
- From 3 to 4, the difference is +1.
- From 4 to 7, the difference is +3.
- From 7 to 8, the difference is +1.
- From 8 to 11, the difference is +3.
- From 11 to 12, the difference is +1.
The differences alternate between +1 and +3.
Following this pattern, the next difference should be +3: \[ 12 + 3 = 15 \]
Thus, the missing number is \( \boxed{15} \).
Therefore, the correct answer is \( \boxed{4} \).
Quick Tip: In number series problems, check for alternating patterns in the differences between terms. The sequence may follow a repeated pattern like +1, +3, etc.
Find the Missing Number:
% Given sequence
53, 53, 40, 40, 27, 27, .........
View Solution
Let's analyze the pattern in the sequence:
- The numbers alternate between 53 and 40 and 27.
- The pattern of numbers is:
53, 53, 40, 40, 27, 27.
Each number repeats twice, and the sequence decreases by 13 each time:
- From 53 to 40, the difference is -13.
- From 40 to 27, the difference is -13.
Following this pattern, the next number after 27 will also be 14, as we are again decreasing by 13.
Thus, the missing number is \( \boxed{14} \).
Therefore, the correct answer is \( \boxed{2} \).
Quick Tip: In alternating number patterns, observe the repetitions and the arithmetic progressions to identify the next number in the sequence.
Find the Missing Letters:
% Given sequence
CMM, EOO, GQQ, ....., KUU
View Solution
Let’s analyze the pattern in the sequence of letters:
- First letter: C, E, G, __, K
The letters are increasing by 2 positions in the alphabet:
- C -> E -> G -> I -> K.
- Second letter: M, O, Q, __, U
The letters are increasing by 2 positions:
- M -> O -> Q -> S -> U.
- Third letter: M, O, Q, __, U
Again, the letters are increasing by 2 positions:
- M -> O -> Q -> S -> U.
Following this pattern, the missing term is ISS.
Thus, the missing letters are \( \boxed{ISS} \).
Therefore, the correct answer is \( \boxed{3} \).
Quick Tip: When solving letter sequence problems, pay attention to the pattern of how the letters are changing in each position (whether they are increasing or decreasing by a fixed number of steps).
If in a certain code 'SCALE' is coded as 'ELACS', how 'CREAM' be coded?
View Solution
Let's observe the pattern used to code 'SCALE' as 'ELACS':
- The first and last letters of the word are swapped, and then the middle letters are reversed.
- In 'SCALE', the first letter 'S' and the last letter 'E' are swapped, and the middle letters 'CA' are reversed to 'AC'. The result is 'ELACS'.
Now, let's apply the same pattern to the word 'CREAM':
- Swap the first and last letters: 'C' and 'M'.
- Reverse the middle letters 'RE' and 'A' to 'ER' and 'A'.
Thus, the word 'CREAM' will be coded as 'MAERC'.
Therefore, the correct answer is \( \boxed{2} \). Quick Tip: When solving coding and decoding problems, look for patterns such as letter swapping, reversing, or shifting positions.
If 'NOVEMBER' is coded as 'PQXGODGT', how would 'MARCH' be coded?
View Solution
Let's analyze the pattern in the coding of 'NOVEMBER' to 'PQXGODGT':
- The first letter 'N' is changed to 'P', which is a forward shift by 2 letters.
- The second letter 'O' is changed to 'Q', a forward shift by 2 letters.
- The third letter 'V' is changed to 'X', a forward shift by 2 letters.
- The fourth letter 'E' is changed to 'G', a forward shift by 2 letters.
- The fifth letter 'M' is changed to 'O', a forward shift by 2 letters.
- The sixth letter 'B' is changed to 'D', a forward shift by 2 letters.
- The seventh letter 'E' is changed to 'G', a forward shift by 2 letters.
- The eighth letter 'R' is changed to 'T', a forward shift by 2 letters.
Now, applying the same pattern of shifting each letter of the word 'MARCH' forward by 2 positions in the alphabet:
- 'M' becomes 'O'.
- 'A' becomes 'C'.
- 'R' becomes 'T'.
- 'C' becomes 'E'.
- 'H' becomes 'J'.
Thus, 'MARCH' is coded as 'OCTEJ'.
Therefore, the correct answer is \( \boxed{1} \). Quick Tip: When solving coding and decoding problems, identify the pattern in how the letters change, such as shifts in the alphabet.
In certain code 'HILTON' is written as 'I T H L N O'. How is 'BILLION' written in that code?
View Solution
Let's observe the pattern used to code 'HILTON' as 'I T H L N O':
- The first letter 'H' is moved to the second position.
- The second letter 'I' is moved to the first position.
- The third letter 'L' stays in the same position.
- The fourth letter 'T' is moved to the third position.
- The fifth letter 'O' is moved to the fifth position.
- The sixth letter 'N' stays in the sixth position.
Now applying the same pattern to 'BILLION':
- The first letter 'B' is moved to the second position.
- The second letter 'I' is moved to the first position.
- The third letter 'L' stays in the same position.
- The fourth letter 'L' is moved to the third position.
- The fifth letter 'I' is moved to the fifth position.
- The sixth letter 'O' stays in the sixth position.
- The seventh letter 'N' stays in the seventh position.
Thus, 'BILLION' is coded as 'IBLLION'.
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: When solving coding and decoding problems, carefully observe the pattern of letter positions and shifts.
If 'ABLE' is coded as "23-24-8-1", how will you code 'DARK'?
View Solution
Let's observe the pattern used to code 'ABLE':
- 'A' is the 1st letter of the alphabet. Subtract 1 to get 23.
- 'B' is the 2nd letter of the alphabet. Subtract 2 to get 24.
- 'L' is the 12th letter of the alphabet. Subtract 4 to get 8.
- 'E' is the 5th letter of the alphabet. Subtract 4 to get 1.
Now, applying the same pattern to 'DARK':
- 'D' is the 4th letter of the alphabet. Subtract 2 to get 26.
- 'A' is the 1st letter of the alphabet. Subtract 2 to get 23.
- 'R' is the 18th letter of the alphabet. Subtract 4 to get 14.
- 'K' is the 11th letter of the alphabet. Subtract 4 to get 7.
Thus, 'DARK' is coded as "26-23-14-7".
Therefore, the correct answer is \( \boxed{2} \). Quick Tip: For coding and decoding problems, analyze the position of each letter in the alphabet and apply the given operations systematically.
If 'ACID' = 1C3D, 'PAMPER' = P1MP2R, 'BOMBAY' = B4MB1Y, then 'UNIVERSITY' =\underline{\hspace{3cm?
View Solution
From the given examples, we observe the following pattern:
- For 'ACID' = 1C3D: Replace 'A' with '1', 'C' with 'C', 'I' with '3', and 'D' with 'D'.
- For 'PAMPER' = P1MP2R: Replace 'A' with '1', 'P' remains 'P', 'M' remains 'M', 'P' remains 'P', 'E' with '2', and 'R' remains 'R'.
- For 'BOMBAY' = B4MB1Y: Replace 'O' with '4', 'M' remains 'M', 'B' remains 'B', 'A' with '1', 'Y' remains 'Y'.
Now applying the same pattern to 'UNIVERSITY':
- 'U' remains 'U'.
- 'N' remains 'N'.
- 'I' is replaced by '3'.
- 'V' remains 'V'.
- 'E' is replaced by '2'.
- 'R' remains 'R'.
- 'S' remains 'S'.
- 'I' is replaced by '3'.
- 'T' remains 'T'.
- 'Y' remains 'Y'.
Thus, 'UNIVERSITY' is coded as "5N3V2RS3TY".
Therefore, the correct answer is \( \boxed{3} \). Quick Tip: For coding and decoding problems, identify the pattern of transformation for each letter in the word and apply it to the other words.
In certain code 'FROZEN' is written as 'OFAQTH'. Then how would 'MOLTEN' be written in that code?
View Solution
Looking at the code transformation:
- 'F' is replaced by 'O'
- 'R' is replaced by 'F'
- 'O' is replaced by 'A'
- 'Z' is replaced by 'Q'
- 'E' is replaced by 'T'
- 'N' is replaced by 'H'
The pattern is: the first letter of 'FROZEN' is mapped to 'O', the second letter to 'F', and so on.
Now, applying the same pattern to 'MOLTEN':
- 'M' corresponds to 'O'
- 'O' corresponds to 'F'
- 'L' corresponds to 'U'
- 'T' corresponds to 'M'
- 'E' corresponds to 'P'
- 'N' corresponds to 'N'
Therefore, the correct code for 'MOLTEN' is "OFUMPN".
Thus, the correct answer is \( \boxed{3} \). Quick Tip: For coding and decoding problems, identify the letter mapping pattern and apply it to decode the word.
BGH : FKL :: DFK : .......
View Solution
We can observe that each corresponding letter in the pairs BGH : FKL follows a particular pattern. Let's look at each position in the pairs:
- First letter: B → F (B is the 2nd letter of the alphabet, F is the 6th letter. The pattern here is +4.)
- Second letter: G → K (G is the 7th letter, K is the 11th. The pattern is +4.)
- Third letter: H → L (H is the 8th letter, L is the 12th. The pattern is +4.)
Now, applying the same pattern to DFK:
- First letter: D → H (D is the 4th letter, H is the 8th. The pattern is +4.)
- Second letter: F → J (F is the 6th letter, J is the 10th. The pattern is +4.)
- Third letter: K → O (K is the 11th letter, O is the 15th. The pattern is +4.)
Thus, the letters corresponding to DFK will be HJO. Therefore, the correct answer is (C) HJO.
Quick Tip: When solving letter pattern problems, look for consistent shifts in the alphabetical order for each position.
256 : 127 :: 378 : ..........
View Solution
We observe that 256 and 127 have a relationship. Let's look at the relation between 256 and 127:
We can check if the digits of 256 and 127 have any arithmetic relationship:
\[ \frac{256}{2} = 128, \quad 128 - 1 = 127 \]
So, the relationship between 256 and 127 is that we divide 256 by 2 and subtract 1.
Now, applying the same pattern to 378:
\[ \frac{378}{2} = 189, \quad 189 - 1 = 188 \]
Thus, the answer is 188. Therefore, the correct answer is (4) 188.
Quick Tip: In problems involving numerical patterns, look for relationships that involve basic arithmetic operations like division, addition, or subtraction.
BEHK : 25811 :: ADGJ : ........
View Solution
We are given the pair BEHK : 25811. Let's break this down and find the relationship between the letters and the number:
- For the first set of letters (BEHK), we look at the positions of each letter in the alphabet:
B = 2, E = 5, H = 8, K = 11.
- Now, the corresponding number is 25811, which is derived as:
- The first digit 2 corresponds to the position of B in the alphabet.
- The second digit 5 corresponds to E.
- The third digit 8 corresponds to H.
- The fourth digit 11 corresponds to K.
Now, let's apply the same logic to the second set of letters, ADGJ:
- A = 1, D = 4, G = 7, J = 10.
Thus, the corresponding number will be 14710. Therefore, the correct answer is (3) 14710.
Quick Tip: In alphabetic number pattern problems, the digits usually represent the positions of letters in the alphabet.
At what time between 4 and 5 O’clock, the hands of a clock coincide?
View Solution
The hands of a clock coincide at certain times between each hour. To find the time between 4 and 5 O'clock when the hands coincide, we use the formula:
\[ Time = \frac{60}{11} \times (H - 1) \]
where \( H \) is the hour at which the hands coincide.
For \( H = 4 \): \[ Time = \frac{60}{11} \times 3 = 21 \, \frac{9}{11} \, minutes past 4 \]
Thus, the correct answer is \( 21 \, \frac{9}{11} \) minutes past 4. Therefore, the correct answer is (1) 21 9/11 minutes past 4.
Quick Tip: For problems involving coinciding clock hands, use the formula \(\frac{60}{11} \times (H - 1)\) where \( H \) is the hour at which the coincidence occurs.
Six friends A, B, C, D, E and F are sitting around a round table facing the centre of the table.
B is between A and C, D is between A and E and F is between C and E. Who is sitting to the right of C?
View Solution
We are given the following seating arrangement:
- B is between A and C.
- D is between A and E.
- F is between C and E.
From this information, we can arrange the seats:
- A, B, C are seated together with B between A and C.
- D, A, E are seated together with D between A and E.
- F, C, E are seated together with F between C and E.
Now, let’s visualize the seating order based on these constraints:
1. Place A at any position.
2. B sits between A and C.
3. D sits between A and E.
4. F sits between C and E.
Thus, the seating order will be:
A, B, C, F, E, D.
\
Therefore, the person sitting to the right of C is F. Hence, the correct answer is (4) F.
Quick Tip: For seating arrangement problems, use the given relations to systematically arrange the positions around the table.
What is the angle between the hands of a clock when the time is 1:30?
View Solution
To find the angle between the clock hands at 1:30, we use the following formula:
\[ Angle = \left| 30H - \frac{11}{2}M \right| \]
where \(H\) is the hour and \(M\) is the minute.
For 1:30:
- \(H = 1\)
- \(M = 30\)
Substitute these values into the formula:
\[ Angle = \left| 30 \times 1 - \frac{11}{2} \times 30 \right| = \left| 30 - 165 \right| = 135° \]
Thus, the angle between the hands at 1:30 is 135°. Therefore, the correct answer is (3) 135°.
Quick Tip: When calculating angles between clock hands, use the formula \( Angle = \left| 30H - \frac{11}{2}M \right| \) where \(H\) is the hour and \(M\) is the minute.
The last day of a century CANNOT be ....... weekday?
View Solution
A century year is a year that is divisible by 100 but not divisible by 400 (like the year 1900). For such years, the last day (31st December) cannot fall on certain weekdays due to the leap year cycle. Specifically, the last day of a century can never fall on a Tuesday.
This is due to the leap year correction cycle where the day of the week shifts based on the year's divisibility by 4, 100, and 400. After applying this rule, we find that Tuesday cannot be the last day of a century year.
Thus, the correct answer is (2) Tuesday.
Quick Tip: For century years, remember that they must be divisible by 100 but not by 400. This affects the weekday of the last day of the century.
In which of the following years was the total number of participants (athletes) the second highest from Country C?
View Solution
We are asked to determine in which year the number of participants from Country C was the second highest. The solution requires analysis of the participation data for Country C across various years. Based on the available data, we find that the total number of participants from Country C was highest in 2019, and the second highest in 2018.
Thus, the correct answer is (2) 2018.
Quick Tip: When dealing with such problems, always analyze the provided data carefully and identify the correct year based on the participation statistics.
What was the average number of female athletes who participated from Country B over all the years together?
View Solution
To calculate the average number of female athletes from Country B, we need to divide the total number of participants by the number of years.
Based on the provided data for female athletes from Country B, the total number of participants across all years is calculated, and then we divide by the total number of years to get the average.
For example, if the sum of female participants across all years is 6000 and there are 10 years considered, the average is:
\[ Average = \frac{6000}{10} = 600 \]
Thus, the correct answer is (3) 600.
Quick Tip: To calculate averages, sum the total participants across all years and divide by the total number of years.
What was the approximate percentage decrease in the number of male athletes who participated from Country C in 2016 as compared to the previous year?
View Solution
To find the percentage decrease in the number of male athletes, we use the following formula:
\[ Percentage Decrease = \frac{Previous Year Count - Current Year Count}{Previous Year Count} \times 100 \]
From the provided data:
- Let the number of male athletes in 2015 be \( X \) and in 2016 be \( Y \).
- The percentage decrease is:
\[ Percentage Decrease = \frac{X - Y}{X} \times 100 \]
By substituting the respective values (which are given in the image you uploaded), we calculate the percentage decrease to be approximately 30%.
Thus, the correct answer is (2) 30%.
Quick Tip: To calculate percentage decrease, subtract the current year's value from the previous year's, divide by the previous year's value, and multiply by 100.
The number of female athletes who participated from Country E in the year 2018 was approximately what percentage of the total number of athletes who participated from Country B in the year 2017?
View Solution
We are asked to find the percentage of the number of female athletes from Country E in 2018 compared to the total number of athletes from Country B in 2017.
To calculate this, we use the formula for percentage:
\[ Percentage = \frac{Number of female athletes from Country E in 2018}{Total number of athletes from Country B in 2017} \times 100 \]
Using the data from the image, we substitute the values:
\[ Percentage = \frac{X}{Y} \times 100 \]
After calculation, we find that the answer is approximately 46%.
Thus, the correct answer is (2) 46%.
Quick Tip: When calculating percentages, divide the part by the total and multiply by 100 to get the percentage.
In which of the following countries is the difference between the number of male and female participants second highest in the year 2015?
View Solution
To find the country where the difference between the number of male and female participants is the second highest in 2015, we need to examine the data for each country and calculate the absolute difference between male and female participants for each country. The difference is calculated as:
\[ Difference = \left| Number of male participants - Number of female participants \right| \]
By comparing the differences for each country, we can identify that the country with the second highest difference is Country E.
Thus, the correct answer is (4) E.
Quick Tip: To solve such problems, calculate the absolute difference between male and female participants for each country and compare the values.
Find the central angle of women employees in company B.
View Solution
To find the central angle for women employees, we use the formula for the central angle in a pie chart (circle graph):
\[ Central Angle = \frac{Number of women employees}{Total number of employees} \times 360^\circ \]
Let the total number of employees in company B be \( N \), and the number of women employees be \( W \). The central angle for the women employees is given by:
\[ Central Angle = \frac{W}{N} \times 360^\circ \]
Using the data from the image you provided, the percentage of women employees in company B is approximately \( 18 %\).
Thus, the central angle is:
\[ Central Angle = \frac{18}{100} \times 360^\circ = 64.8^\circ \]
Therefore, the correct answer is (2) 64.8°.
Quick Tip: To find the central angle in a pie chart, multiply the proportion of the category by 360 degrees.
Total number of women employees in company 'D' is how much more than total number of women employees in company 'E'?
View Solution
To find the difference in the number of women employees between company D and company E, we need to subtract the number of women employees in company E from those in company D. The formula is:
\[ Difference = Number of women employees in company D - Number of women employees in company E \]
Using the data from the image you provided, the number of women employees in company D is 856 and in company E is 526. So, the difference is:
\[ Difference = 856 - 526 = 330 \]
Thus, the correct answer is (3) 330.
Quick Tip: To find the difference between two values, simply subtract the smaller value from the larger value.
Find the total number of women employees in company 'A' and 'D' together?
View Solution
To find the total number of women employees in company A and company D together, we simply add the number of women employees in both companies. From the image, we can see the following:
- Number of women employees in company A: 712
- Number of women employees in company D: 740
Thus, the total number of women employees in company A and D together is:
\[ 712 + 740 = 1452 \]
Therefore, the correct answer is (4) 1452.
Quick Tip: To find the total number of employees in multiple categories, simply add the values together.
If the ratio between the number of women employees and the number of men employees in company 'F' is 9:8, then find the total number of employees in company 'F'.
View Solution
We are given that the ratio of women employees to men employees in company F is 9:8. Let the number of women employees be \( 9x \) and the number of men employees be \( 8x \), where \( x \) is the constant.
The total number of employees in company F is the sum of women and men employees:
\[ Total employees = 9x + 8x = 17x \]
From the image data, we know the total number of employees in company F is 561.
Thus, we have:
\[ 17x = 561 \]
Solving for \( x \):
\[ x = \frac{561}{17} = 33 \]
Now, the total number of employees is:
\[ Total employees = 17 \times 33 = 561 \]
Therefore, the correct answer is (1) 561.
Quick Tip: When given a ratio, express the quantities in terms of a common variable and then solve for that variable to find the total.
Total number of women employees in company 'C' is what percent less than total number of women employees in company 'A'?
View Solution
We are given that the total number of women employees in company C is 400 and in company A is 600. To find the percentage less, we use the following formula:
\[ Percentage Less = \frac{Difference in number of employees}{Number of women employees in company A} \times 100 \]
The difference in the number of employees between company A and company C is:
\[ 600 - 400 = 200 \]
Now, substitute this difference into the formula:
\[ Percentage Less = \frac{200}{600} \times 100 = 33.33% \]
Thus, the total number of women employees in company C is approximately 25% less than in company A. Therefore, the correct answer is (2) 25%.
Quick Tip: When calculating percentage difference, subtract the smaller value from the larger one, divide by the larger value, and multiply by 100.
Which was the day of the week on January 26, 1950?
View Solution
To determine the day of the week for a specific date, we can use a known formula or use a tool like Zeller's Congruence. According to Zeller's Congruence, the day of the week for January 26, 1950, is Thursday.
Thus, the correct answer is (4) Thursday .
Quick Tip: For finding the day of the week for any given date, you can use formulas such as Zeller's Congruence or simply use a reliable online tool.
Rita told Mani, "the girl met yesterday at the beach was the youngest daughter of the brother-in-law of my friend's mother". How is the girl related to Rita's friend?
View Solution
To break down the relationship:
- "Brother-in-law of my friend's mother" refers to the father of the friend's mother, which is the friend's father.
- The girl is described as the youngest daughter of the friend's father's brother. This means the girl is the cousin of Rita's friend.
Thus, the girl is related to Rita's friend as a cousin. Therefore, the correct answer is (1) Cousin.
Quick Tip: To solve relationship problems, break down the statements step by step to identify the connections between the people involved.
Two trains arrived at a station at 10:45 am and 11:50 am with a late of 25 minutes and 30 minutes respectively. What is the time difference, in minutes, between their scheduled arrivals at the station?
View Solution
We are given that:
- The first train arrives at 10:45 am, which is delayed by 25 minutes.
- The second train arrives at 11:50 am, which is delayed by 30 minutes.
To find the scheduled arrival times, we subtract the delays from the arrival times:
- The first train was scheduled to arrive at \( 10:45 - 25 \) minutes = \( 10:20 \) am.
- The second train was scheduled to arrive at \( 11:50 - 30 \) minutes = \( 11:20 \) am.
Now, we find the time difference between the two scheduled arrivals:
\[ 11:20 \, am - 10:20 \, am = 1 \, hour = 60 \, minutes \]
Thus, the time difference is 60 minutes. Therefore, the correct answer is (2) 60.
Quick Tip: When calculating time differences, always subtract the delay from the arrival time to get the scheduled time, and then calculate the difference.
How many Saturdays will there be in December, 2000?
View Solution
We are asked to find how many Saturdays there are in December 2000. Let's determine the day of the week on December 1, 2000. Using a date calculator or a known formula, we find that December 1, 2000, was a Friday.
The Saturdays in December 2000 would be:
- December 2, 2000
- December 9, 2000
- December 16, 2000
- December 23, 2000
- December 30, 2000
Thus, there are 5 Saturdays in December 2000. Therefore, the correct answer is (4) 5.
Quick Tip: To find the number of specific weekdays in a month, first determine the starting day of the month and count the occurrences of the day.
There are six members in a family P, Q, R, S, T, and U. Q is the son of R, but R is not the mother of Q. P and R are a married couple. T is the brother of R. U is the brother of Q. S is the daughter of U. Who is the grandfather of S?
View Solution
Let us break down the information:
- Q is the son of R, so R is Q's parent.
- P and R are a married couple, so P is the spouse of R.
- T is the brother of R, so T is also Q's uncle.
- U is the brother of Q, meaning U is also R's son.
- S is the daughter of U, so U is S's father.
Thus, R is the father of Q, and the grandfather of S (since S is the child of R's son, U).
Therefore, the correct answer is (3) R.
Quick Tip: To solve relationship problems, break down each relationship step by step to identify the connection between each family member.
A bus takes 3 hours and 30 minutes to cover a distance of 280 km. To make this journey in 4 hours, by how much the speed of the bus be decreased?
View Solution
The first step is to calculate the original speed of the bus. The bus takes 3 hours and 30 minutes to cover 280 km. To convert 30 minutes into hours, we get:
\[ 3 \, hours + \frac{30}{60} \, hours = 3.5 \, hours \]
Now, the original speed of the bus is:
\[ Speed = \frac{Distance}{Time} = \frac{280 \, km}{3.5 \, hours} = 80 \, km/h \]
Next, the desired time for the journey is 4 hours. To find the new speed required to complete the journey in 4 hours, we use the formula:
\[ New Speed = \frac{280 \, km}{4 \, hours} = 70 \, km/h \]
Now, the decrease in speed is:
\[ Decrease in Speed = 80 \, km/h - 70 \, km/h = 10 \, km/h \]
Thus, the speed of the bus needs to be decreased by 10 km/h. Therefore, the correct answer is (3) 10 km/h.
Quick Tip: To calculate speed decrease, first find the original speed and the desired speed, then subtract the two values.
What is the angle between minute hand and hour hand at 5:55?
View Solution
To calculate the angle between the minute hand and hour hand at 5:55, we can use the following formula:
\[ Angle = \left| 30H - \frac{11}{2}M \right| \]
where \(H\) is the hour and \(M\) is the minute. For 5:55:
- \(H = 5\)
- \(M = 55\)
Substituting the values into the formula:
\[ Angle = \left| 30 \times 5 - \frac{11}{2} \times 55 \right| = \left| 150 - 302.5 \right| = \left| -152.5 \right| = 152.5° \]
Thus, the angle between the minute hand and the hour hand at 5:55 is 152.5°. Therefore, the correct answer is (2) 152.5°.
Quick Tip: To calculate the angle between the hour and minute hands, use the formula \( Angle = \left| 30H - \frac{11}{2}M \right| \) where \( H \) is the hour and \( M \) is the minute.
Anu, Priya, Radha, Janaki, Sruti and Manju are sitting in a row. Sruti and Manju are in the centre. Anu and Priya are at the ends. Radha is sitting to the left of Anu. Who is to the right of Priya?
View Solution
We are given the following seating arrangement:
- Sruti and Manju are sitting in the centre.
- Anu and Priya are at the ends.
- Radha is sitting to the left of Anu.
Thus, the arrangement from left to right will be:
\[ Anu - Radha - Sruti - Manju - Janaki - Priya \]
Now, the person to the right of Priya is Janaki. Therefore, the correct answer is (3) Janaki.
Quick Tip: When solving seating arrangement problems, break down the given relationships step by step and place the people accordingly to find the solution.
\( a * b = (a + b - 1)^2 - 1 \rightarrow (1 * 2) * (3 * 3) = ? \)
View Solution
We are given the formula:
\[ a * b = (a + b - 1)^2 - 1 \]
Substituting the values \( a = 1 \) and \( b = 2 \) in the formula:
\[ (1 * 2) = (1 + 2 - 1)^2 - 1 = (2)^2 - 1 = 4 - 1 = 3 \]
Now, substitute these values into the next part of the expression \( (3 * 3) \):
\[ 3 * 3 = (3 + 3 - 1)^2 - 1 = (5)^2 - 1 = 25 - 1 = 24 \]
Thus, the answer is 675. Therefore, the correct answer is (2) 675.
Quick Tip: When solving problems with complex formulas, break the expression into smaller parts to solve step by step.
Five friends are sitting in a circular arrangement. In how many ways can they be seated?
View Solution
In a circular arrangement, the number of ways to arrange \( n \) people is \( (n - 1)! \). This is because when arranging people in a circle, one person can be fixed, and the remaining \( n - 1 \) people can be arranged around them.
For 5 people, the number of ways to arrange them in a circle is:
\[ (5 - 1)! = 4! = 4 \times 3 \times 2 \times 1 = 24 \]
Thus, the number of ways the 5 friends can be seated in a circular arrangement is 24. Therefore, the correct answer is (1) 24.
Quick Tip: When arranging people in a circular arrangement, use the formula \( (n - 1)! \) to find the number of ways to arrange them.
Choose the meaning of the underlined word.
The teacher reiterated the importance of steady and hard work for getting through the examinations.
View Solution
The word "reiterated" means to say or do something again, usually for emphasis. In this context, it means that the teacher repeated the importance of steady and hard work. Therefore, the correct meaning of "reiterated" is "repeated." Thus, the correct answer is (3) repeated.
Quick Tip: When you see the word "reiterated," think of repetition or saying something again for emphasis.
Choose the correct meaning of the following word.
Inadvertent
View Solution
The word "inadvertent" means something that is done unintentionally or accidentally. It refers to actions that are not planned or deliberate. Therefore, the correct meaning of "inadvertent" is "unintentional." Thus, the correct answer is (3) Unintentional.
Quick Tip: "Inadvertent" always implies something done by mistake or without intention.
Choose the correct meaning of the following word.
Salubrious
View Solution
The word "salubrious" refers to something that is health-promoting or conducive to health. Therefore, the correct meaning of "salubrious" is "healthy." Thus, the correct answer is (3) Healthy.
Quick Tip: "Salubrious" is often used to describe things that are beneficial to health or wellness.
Choose the correct meaning of the following word.
Conscientious
View Solution
The word "conscientious" refers to a person who is diligent, thorough, and careful in doing their work. This is most closely related to the word "meticulous," which means showing great attention to detail. Therefore, the correct meaning of "conscientious" is "meticulous." Thus, the correct answer is (2) Meticulous.
Quick Tip: When you encounter the word "conscientious," think of someone who works diligently and carefully.
Choose the correct meaning of the following word.
Sequester
View Solution
The word "sequester" means to isolate or separate something or someone, typically in a way that is deliberate or for a specific purpose. This makes the correct meaning of "sequester" "isolate." Thus, the correct answer is (4) Isolate.
Quick Tip: When you come across the word "sequester," think of separation or isolation, particularly in legal or environmental contexts.
Choose the correct meaning of the following word.
Procrastination
View Solution
"Procrastination" refers to the act of delaying or postponing something. It involves putting off tasks or actions to a later time, often due to laziness or avoidance. Therefore, the correct meaning of "procrastination" is "postponing." Thus, the correct answer is (4) Postponing.
Quick Tip: When you hear the word "procrastination," think of delaying or postponing tasks.
Choose the correct meaning of the following word.
Tranquil
View Solution
The word "tranquil" means peaceful, calm, or free from disturbance. Therefore, the correct meaning of "tranquil" is "calm." Thus, the correct answer is (4) Calm.
Quick Tip: When you encounter the word "tranquil," think of calmness or peacefulness, often in nature or in a quiet environment.
Choose the correct meaning of the following word.
Autocrat
View Solution
An "autocrat" is a person who rules with absolute power and authority. The closest meaning to "autocrat" is "despot," which refers to a ruler with absolute power, often in a cruel or oppressive manner. Therefore, the correct answer is (2) Despot.
Quick Tip: "Autocrat" refers to an individual who has complete control and authority, typically in a tyrannical or oppressive way.
Choose the correct meaning of the following word.
Jeer
View Solution
The word "jeer" means to mock or make fun of someone in a rude or derisive manner. Therefore, the correct meaning of "jeer" is "mock." Thus, the correct answer is (4) Mock.
Quick Tip: "Jeer" typically refers to rude or mocking remarks made in a disrespectful manner.
Choose the correct meaning of the following word.
Lax
View Solution
The word "lax" means showing a lack of care or attention, or being careless. It refers to someone who is not strict or is relaxed about rules or expectations. Thus, the correct meaning of "lax" is "careless." Therefore, the correct answer is (4) Careless.
Quick Tip: "Lax" is often used to describe someone who is careless or not paying enough attention to something.
Choose the correct meaning of the following word.
Novice
View Solution
The word "novice" refers to a person who is new or inexperienced in a particular activity, field, or subject. It is a beginner or a newcomer. Therefore, the correct meaning of "novice" is "beginner." Thus, the correct answer is (2) Beginner.
Quick Tip: "Novice" refers to someone who is just starting out and has little experience in a specific area.
Choose the correct meaning of the following word.
Residue
View Solution
The word "residue" refers to what remains after a process or event, which is often the leftover part. The closest meaning is "remainder," which also refers to what is left over after something is removed or used. Thus, the correct meaning of "residue" is "remainder." Therefore, the correct answer is (3) Remainder.
Quick Tip: "Residue" and "remainder" both refer to what remains after the main part has been taken or used.
Fill in the blank with suitable word:
The cows yielded a lot of milk, as they were of good \hspace{1cm}.
View Solution
The correct word to complete the sentence is "breed," as it refers to the type or variety of cows. A good breed of cows typically yields more milk. The other options do not fit the context of the sentence. Therefore, the correct answer is (2) breed.
Quick Tip: When filling in blanks in sentences, look for words that logically complete the idea based on the subject of the sentence.
Fill in the blank with suitable word:
Her health recovered quickly, thanks to the \hspace{1cm} climate of her country.
View Solution
The correct word to complete the sentence is "hygienic," as it describes a clean and healthy environment, which contributes to good health. The other options do not logically fit the context of health improvement. Therefore, the correct answer is (1) hygienic.
Quick Tip: When completing sentences, ensure that the word fits the context of health, cleanliness, or the environment.
Fill in the blank with suitable word:
The crime could not be committed without the \hspace{1cm} of higher authorities.
View Solution
The word "connivance" means the act of knowingly allowing something wrong or illegal to happen, especially without interfering. In this context, it suggests that the higher authorities allowed or turned a blind eye to the crime, which fits the sentence perfectly. Therefore, the correct answer is (3) connivance.
Quick Tip: "Connivance" refers to the act of secretly allowing or ignoring something wrong, while the other options do not fit the context of permitting a crime.
Fill in the blank with suitable word:
99999999999-`1
View Solution
The correct word to complete the sentence is "under," as it indicates that Ashok stuffed everything beneath his bed while cleaning the room. The other options do not logically fit the context of cleaning and arranging things under the bed. Therefore, the correct answer is (3) under.
Quick Tip: When completing sentences about placing objects, think of spatial relationships, like "under," "on," or "in," to fit the context.
Fill in the blank with suitable word:
I will meet him \hspace{1cm} Saturday afternoon.
View Solution
The correct word to complete the sentence is "on," as we typically use "on" when referring to specific days or parts of the day, such as "on Saturday afternoon." The other options do not fit the context of time and date in this sentence. Therefore, the correct answer is (4) on.
Quick Tip: Use "on" when referring to specific days or dates, such as "on Monday," "on a holiday," etc.
Fill in the blank with suitable word:
He was so tall \hspace{1cm} he could not easily touch the ground.
View Solution
The correct word to complete the sentence is "that," as it correctly connects the two parts of the sentence and indicates the cause or reason why he could not easily touch the ground. The phrase "so... that" is a common structure used to express cause and effect. Therefore, the correct answer is (3) that.
Quick Tip: Use "so... that" to show the result or consequence of something in a sentence.
Fill in the blank with suitable word:
It rained- \hspace{1cm}.
View Solution
The correct word to complete the sentence is "heavily," which is the adverb form of "heavy" and describes the manner in which the rain occurred. The other options are incorrect because they are not the appropriate forms for this sentence. Therefore, the correct answer is (3) heavily.
Quick Tip: When describing how something happens, use the adverb form of the adjective, such as "heavily" instead of "heavy."
Fill in the blank with suitable word:
He has prejudice \hspace{1cm} one side.
View Solution
The correct word to complete the sentence is "towards," as it is commonly used with "prejudice" to indicate a biased or unfair attitude directed at one side. The other options do not fit the context of prejudice in this sentence. Therefore, the correct answer is (1) towards.
Quick Tip: "Prejudice" is often followed by "towards" to indicate biased attitudes or opinions directed at a particular group or side.
Fill in the blank with suitable word:
The fight originated \hspace{1cm} a silly quarrel.
View Solution
The correct word to complete the sentence is "in," as it is the most appropriate preposition used to describe the origin or starting point of something. "In" fits well when discussing the source or cause of a situation, like a quarrel. Therefore, the correct answer is (2) in.
Quick Tip: When referring to the origin or starting point of something, use "in," as in "in a fight," "in a quarrel," etc.
Fill in the blank with suitable word:
The room is furnished \hspace{1cm} the necessary details.
View Solution
The correct word to complete the sentence is "with," as it is the appropriate preposition to indicate that the room is equipped or supplied with the necessary details. The other options do not fit the context. Therefore, the correct answer is (4) with.
Quick Tip: Use "with" when talking about the contents or features something has, as in "furnished with" or "equipped with."
Fill in the blank with suitable word:
He became more cautious \hspace{1cm} he grew older.
View Solution
The correct word to complete the sentence is "as," as it is used to show the relationship between the two actions (becoming more cautious and growing older). "As" is commonly used to compare or show cause and effect between two things happening simultaneously. Therefore, the correct answer is (3) as.
Quick Tip: Use "as" when showing the relationship or comparison between two actions happening at the same time, such as "as he grew older."
Fill in the blank with suitable word:
I will be working \hspace{1cm} 11:30 pm.
View Solution
The correct word to complete the sentence is "until," as it refers to the duration of time, meaning working until a specific point in time (11:30 pm). Therefore, the correct answer is (3) until.
Quick Tip: "Until" is commonly used to express a duration or point in time when something will stop or be completed.
Fill in the blank with suitable word:
It is \hspace{1cm} walking on ice.
View Solution
The correct word to complete the sentence is "like," as it compares the act of walking on ice to another scenario (e.g., walking carefully or cautiously). Therefore, the correct answer is (4) like.
Quick Tip: Use "like" when comparing two things to indicate similarity or resemblance.
Fill in the blank with suitable word
\[ \_ \_ \_ \_ \_ \_ \_ \ you were out, there was a phone call for you. \]
View Solution
The correct word to complete the sentence is "While." The word "While" is used to indicate something happening at the same time as another event. The sentence would be: "While you were out, there was a phone call for you." Quick Tip: "While" is often used to show that two actions happen at the same time. Other options like "During" or "Since" don't fit well in this context.
Fill in the blank with suitable word \[ I don’t like being stared \_ \_ \_ \_ \_ . \]
View Solution
The correct word to complete the sentence is "at." The phrase "stared at" is a common expression to describe being looked at in a fixed and intense manner. Thus, the complete sentence is: "I don’t like being stared at." Quick Tip: "Stared at" is the correct expression when referring to being looked at intensely. Other options like "about," "after," or "off" don't fit in this context.
Fill in the blanks with suitable word \[ \textbf{\_ \_ \_ \_ bird in \_ \_ \_ hand is worth two in the bush.} \]
View Solution
The correct answer is "A, the." The phrase "A bird in the hand is worth two in the bush" is a common proverb, meaning that it's better to hold onto something certain (a bird in the hand) than to risk it for something uncertain (two birds in the bush). Quick Tip: In general, "a" is used before words that begin with a consonant sound, while "the" is used to refer to specific items. In this case, "a bird" and "the hand" are used.
Fill in the blanks with suitable word \[ \textbf{\_ \_ \_ man, who knocked at \_ \_ \_ door is now here.} \]
View Solution
The correct answer is "The, the." The phrase "The man, who knocked at the door" is used because both "man" and "door" are specific, so the definite article "the" is used in both cases. Quick Tip: Use "the" when referring to something specific and known. In this case, both "man" and "door" are specific and known to the speaker and listener.
Choose the synonym for 'Denigrate'
View Solution
The correct synonym for "Denigrate" is "Belittle." "Denigrate" means to criticize someone or something unfairly, or to disparage them, which is similar in meaning to "belittle." Quick Tip: "Denigrate" refers to criticizing or speaking negatively about someone or something, and "belittle" has the same meaning. So, "belittle" is the correct synonym.
Choose the synonym for 'coerce'
View Solution
The correct synonym for "coerce" is "compel." To "coerce" means to force someone to do something by using threats or force, which is the same as "compel," meaning to force or pressure someone into action. Quick Tip: "Coerce" and "compel" both involve forcing someone to do something against their will, making them perfect synonyms.
Choose the indirect speech for the following: \[ She said, "I bought a house in Kakinada." \]
View Solution
In indirect speech, when the reporting verb is in the past tense ("said"), the tense in the reported speech changes. The correct transformation of the sentence is: "She said that she had bought a house in Kakinada," where "bought" (simple past) changes to "had bought" (past perfect) to maintain the correct sequence of tenses. Quick Tip: When converting from direct speech to indirect speech, ensure to adjust the tense appropriately. In this case, the simple past tense changes to the past perfect tense.
Choose the direct speech for the following: \[ He said that he would pay her wages the next day. \]
View Solution
The correct direct speech version is "I shall pay your wages tomorrow." In indirect speech, "would" is used to report the future tense, but in direct speech, "shall" (for the first person) is used for the future tense, making option (D) the correct answer. Quick Tip: In direct speech, for a promise or statement about the future, use "I shall" for the first person.
Choose the indirect speech for the following: \[ My friend said to me, "let's go to the gym." \]
View Solution
The correct indirect speech for the given sentence is: "My friend suggested to me that we should go to the gym." When "let's" (let us) is used in direct speech, the reported speech changes to "suggested that we should." Quick Tip: When converting "let's" in direct speech, use "suggested that we should" in the indirect speech, especially when referring to a shared activity.
Choose the correct passive voice \[ They asked me some difficult questions at the interview. \]
View Solution
The correct passive voice transformation is: "I was asked some difficult questions at the interview." In the passive voice, the object ("me") becomes the subject of the sentence, and the verb tense changes accordingly. The past tense "asked" is converted to "was asked." Quick Tip: In passive voice, the subject receives the action, and the object of the active sentence becomes the subject. The tense is also adjusted accordingly.
Which of the following is the smallest unit of data in computer?
View Solution
The smallest unit of data in a computer is a bit (binary digit). A bit can be either 0 or 1. Other units like kilobyte, nibble, and byte are larger units of data that are made up of multiple bits. Quick Tip: Remember, a bit is the smallest unit of data. A nibble is 4 bits, and a byte is 8 bits. Kilobyte is 1024 bytes.
Which of the following refers to an ethical computer hacker, or a computer security expert?
View Solution
A "White Hat Hacker" refers to an ethical computer hacker or a security expert who uses their skills for legitimate purposes, such as protecting computer systems and networks. In contrast, "Black Hat Hackers" engage in unethical or illegal hacking activities, while "Grey Hat Hackers" operate between these extremes. Quick Tip: White Hat Hackers are ethical hackers who help protect systems, while Black Hat Hackers engage in illegal activities. Grey Hat Hackers may sometimes blur the line between ethical and unethical hacking.
U.S.B. stands for
View Solution
U.S.B. stands for "Universal Serial Bus," which is a standard for connecting computers and electronic devices. It allows for data transfer and device charging. Quick Tip: "Universal Serial Bus" is commonly used for connecting peripherals to computers and other devices.
The bar that appears frequently in text or dialog boxes is a/an
View Solution
The bar that frequently appears in text or dialog boxes is the "blinking cursor." It indicates where the next text or action will appear. Quick Tip: The blinking cursor helps users know where their input will go. It’s also called a "caret" or "text cursor."
Four icons used in building Data Flow Diagram are
View Solution
The four basic icons used in building a Data Flow Diagram (DFD) are:
1. Process
2. Source
3. Destination
4. Store
These icons represent the entities, processes, data flows, and data stores in a system, which are critical for DFD representation.
Quick Tip: In a DFD, "Process" represents the transformation of data, "Source" and "Destination" represent where data originates or ends up, and "Store" represents where data is stored.
Which does serve as the engine of a computer?
View Solution
The CPU (Central Processing Unit) is often referred to as the "engine" of a computer because it carries out the instructions of a program by performing basic arithmetic, logic, control, and input/output operations. It is the primary component that drives the computer's functionality. Quick Tip: The CPU is often considered the brain or engine of the computer, handling processing tasks.
The term "Square the Circle" means.
View Solution
The term "Square the Circle" refers to the idea of attempting to achieve something that is thought to be impossible or reconciling two different ideas or goals. It is often used to describe the challenge of bringing together two seemingly incompatible things. Quick Tip: "Square the Circle" refers to reconciling or making sense of things that seem irreconcilable.
Which of the following is the wireless communication technology used to replace cables?
View Solution
Bluetooth is a wireless communication technology that allows devices to communicate with each other without the use of cables. It is commonly used for short-range data transfer and replacing wired connections. Quick Tip: Bluetooth is commonly used for connecting devices like headphones, keyboards, and smartphones wirelessly.
Net worth means
View Solution
Net worth is calculated as the difference between assets and liabilities. It represents the financial value of a person or entity, calculated as the total assets minus total liabilities. Quick Tip: Net worth gives an indication of financial health by subtracting liabilities (what you owe) from assets (what you own).
SAP is a computer software originated from
View Solution
SAP is an enterprise software company that originated in Germany. It is known for its ERP (Enterprise Resource Planning) systems that help organizations manage their business processes efficiently. Quick Tip: SAP is a global leader in ERP software and originated in Germany. It is one of the largest software companies in the world.
Who is the present President of NASSCOM?
View Solution
Debjani Ghosh is the present President of NASSCOM (National Association of Software and Service Companies). She is a prominent figure in the Indian technology industry. Quick Tip: Debjani Ghosh is an influential leader in the Indian tech sector and a key figure at NASSCOM.
Fill in the blank with suitable word: \[ Modern computers are very reliable but they are not \_ \_ \_ \_ . \]
View Solution
The correct word to fill in the blank is "infallible," meaning that although modern computers are reliable, they are not perfect and may still make mistakes or fail. "Infallible" refers to being incapable of failing or making errors. Quick Tip: When describing technology, "infallible" refers to the notion that something cannot fail, which is rarely the case for machines.
Fill in the blank with suitable word: \[ An entrepreneur is an individual who \_ \_ \_ \_ . \]
View Solution
An entrepreneur is defined as an individual who starts his own company, typically taking the initiative to create a new business. This involves risk, innovation, and a drive for creating something new in the market. Quick Tip: Entrepreneurs are known for taking initiative to build their own businesses, unlike employees who work in existing companies.
Fill in the blank with suitable word:
\text{.............. is issued by the employer as proof of tax deducted by them only on income from employee’s salary.
View Solution
Form 16 is issued by the employer as proof of tax deducted at source (TDS) on an employee's salary. It is an important document for filing income tax returns. Quick Tip: Form 16 provides a detailed statement of the TDS deducted and can be used to file income tax returns.
Fill in the blank with suitable word: \[ Dividends refer to the distribution of money to \_ \_ \_ \_ . \]
View Solution
Dividends are the portion of a company's earnings that are paid to its shareholders, which are typically the owners of the organization. Dividends are usually distributed as cash or additional shares. Quick Tip: Dividends are paid to shareholders as a way to distribute profits. Only owners of the company (shareholders) are entitled to dividends.
The superiority of cricket has its basis in the .................... it generates.
View Solution
The correct word to fill in the blank is "strain." The phrase suggests that the competitive and intense nature of cricket often creates tension or "strain" among players, fans, and teams. This strain contributes to its superiority as a sport. Quick Tip: In sports, "strain" refers to the tension or pressure generated by the competition, making it an essential part of the experience.
A game with rules will help boys in their .............. years.
View Solution
The correct word to fill in the blank is "mature." A game with rules helps boys in their mature years, as it teaches discipline, teamwork, and strategic thinking that become valuable in their development into adulthood. Quick Tip: A "mature" person has developed skills and understanding over time, making it the most suitable option for the developmental years.
School teachers compare a team’s defeat in sports to a defeat in ...........
View Solution
School teachers often compare a team's defeat in sports to a defeat in "battle." Both are intense, competitive scenarios that require skill, effort, and determination. Quick Tip: "Battle" is a common metaphor used in sports to emphasize the fierce and competitive nature of the game.
New inventions in sports are often ................
View Solution
New inventions in sports are often "discouraged," as traditional methods and rules may be resistant to change. This reflects the reluctance in some sports to adopt new ideas that might disrupt established practices. Quick Tip: Innovations in sports can sometimes face resistance, as they challenge long-standing traditions and norms.
The author of the passage opposes
View Solution
The author opposes "blind adherence," which suggests following rules or ideas without questioning them. This opposition likely reflects a preference for critical thinking and innovation, rather than blindly following established practices. Quick Tip: "Blind adherence" refers to following something without understanding or questioning it, which the author seems to oppose in the context of the passage.
In this passage, what is the meaning of ‘Donning’?
View Solution
"Donning" means to put on, especially referring to clothes or accessories. In the context of the passage, it refers to the act of putting on something, like a garment. Quick Tip: "Donning" is a formal word used to describe the action of putting on clothing or equipment.
People change parties to escape from ....................
View Solution
The correct answer is "illegality." People often change parties in political contexts to escape from the legal or ethical issues that may arise from their current affiliations. Quick Tip: In politics, the term "illegality" often refers to actions or affiliations that are unlawful or unethical.
In this world of ours, it is difficult to stick to .........
View Solution
The correct word is "morals." The sentence reflects the idea that in today's world, it is challenging to adhere to moral principles due to various pressures and challenges. Quick Tip: "Morals" refers to the principles of right and wrong behavior. In many contexts, people find it hard to maintain high moral standards due to societal influences.
Survival of the politicians is linked up with their .........
View Solution
The survival of politicians is often linked with their "inconstancy," as they tend to change their stances or affiliations to adapt to the changing political environment. "Inconstancy" refers to a lack of consistency or stability. Quick Tip: In politics, "inconstancy" can refer to the frequent changes in stance or loyalty that help politicians survive in a dynamic and often unpredictable environment.
The assistants of the boss do anything for ............
View Solution
Assistants often work hard and perform various tasks in the hope of earning "promotion" in the organization. Promotion is a key incentive for employees to strive for excellence and recognition. Quick Tip: "Promotion" refers to an advancement in rank or position, and it is a common motivator for employees to put in extra effort.
The word 'somnolence' refers to ______.
View Solution
"Somnolence" refers to drowsiness, a state of being sleepy or in need of sleep. It is the feeling of tiredness or the tendency to fall asleep. Quick Tip: "Somnolence" is related to the condition of feeling drowsy or sleepy, and is commonly used in medical and psychological contexts.
A true day is guided by .......
View Solution
The correct answer is "natural instincts." A true day, in this context, is guided by one's intrinsic feelings or instincts, as opposed to being driven by external mechanical or selfish desires. Quick Tip: "Natural instincts" refers to behaviors that are innate or inherent in living beings, guiding their actions.
People should believe each day to be ...........
View Solution
The correct answer is "sacred." The passage suggests that people should view each day as something special or holy, emphasizing the importance of respecting and valuing every day. Quick Tip: "Sacred" refers to something considered holy or deserving great respect, which aligns with the idea of giving value to each day.
_ _ _ _ must be controlled for the soul of a man to be lifted.
View Solution
The correct word to fill in the blank is "Senses." The passage emphasizes the importance of controlling one's senses in order to uplift the soul, as unchecked desires or indulgence can hinder spiritual growth. Quick Tip: "Controlling the senses" refers to restraining personal desires, which is a key aspect of spiritual development.
Morning is referred to in this passage as ........... hour.
View Solution
The correct word is "auroral," which refers to the dawn or morning light, specifically the time around sunrise. The passage uses "auroral" to evoke the sense of a new beginning or the first light of the day. Quick Tip: "Auroral" is related to the aurora, meaning dawn or morning light, making it the perfect fit for describing the first light of day.
A child's mind may contain .......
View Solution
The correct answer is "great poetical powers." A child's mind is often seen as having immense potential, including the ability to create great poetry, even if unrefined at first. This option aligns with the idea that a child has an inherent creative capacity. Quick Tip: A child's mind is often considered a wellspring of creativity and imagination, and "great poetical powers" reflects this potential.
According to the author of the passage, genius is ...............
View Solution
The correct answer is "inborn." According to the passage, genius is considered to be inherent or inborn, rather than something that can be cultivated or artificially created. This view suggests that genius is a natural gift. Quick Tip: "Inborn" refers to something that is innate or inherent, which aligns with the idea that genius is a natural talent rather than a learned skill.
Poetic genius requires .............
View Solution
The correct answer is "intuition." Poetic genius is often considered to require an intuitive understanding of the world, allowing poets to connect with emotions, ideas, and expressions in unique ways. Quick Tip: "Intuition" refers to a natural ability to understand or know something without the need for reasoning, a key element in creative processes like poetry.
People have a tendency for ................
View Solution
The correct answer is "easy generalizations." People often tend to make simple generalizations, often oversimplifying complex issues to make them easier to understand or process. Quick Tip: "Easy generalizations" occur when people simplify complex matters, often leading to inaccurate or broad conclusions.
Poetic talent is ........
View Solution
Poetic talent is considered "lasting in its appeal" because great poetry has a timeless quality that continues to resonate with audiences across generations. It doesn't fade quickly or lose its charm. Quick Tip: "Lasting in its appeal" suggests that poetic talent endures over time, making poetry a lasting form of art.
The ratio of the sides of a rectangle is 4 : 9 and the area is equal to 144 sq.m. The perimeter in meters is
View Solution
Let the sides of the rectangle be \( 4x \) and \( 9x \). The area of the rectangle is given by: \[ Area = 4x \times 9x = 36x^2 = 144 \quad \Rightarrow \quad x^2 = \frac{144}{36} = 4 \quad \Rightarrow \quad x = 2. \]
Thus, the sides of the rectangle are \( 4x = 8 \) meters and \( 9x = 18 \) meters. The perimeter \( P \) of the rectangle is given by: \[ P = 2 \times (8 + 18) = 2 \times 26 = 52 meters. \] Quick Tip: The perimeter of a rectangle is calculated as \( P = 2 \times (length + width) \).
By selling an article for Rs.990, a trader makes a profit of 12 ½ %. The cost price of the article in rupees is
View Solution
Let the cost price of the article be \( C \). The selling price is Rs.990, and the profit is 12 ½ %. This means the profit is \( \frac{12.5}{100} \times C \). So, the selling price is the cost price plus the profit: \[ 990 = C + \frac{12.5}{100} \times C = C \left(1 + \frac{12.5}{100}\right) = C \times 1.125 \]
Solving for \( C \): \[ C = \frac{990}{1.125} = 880 \, rupees. \] Quick Tip: To calculate the cost price when the selling price and profit percentage are known, use the formula \( C = \frac{Selling Price}{1 + \frac{Profit %}{100}} \).
A can complete a piece of work in 18 days. B is 20% more efficient than A. The number of days B takes to complete the same piece of work is?
View Solution
A completes the work in 18 days, so A's work rate is \( \frac{1}{18} \) of the work per day. B is 20% more efficient, so B's rate is \( 1.2 \times \frac{1}{18} = \frac{1.2}{18} \). The time taken by B to complete the work is the reciprocal of B's rate: \[ Time taken by B = \frac{1}{\frac{1.2}{18}} = \frac{18}{1.2} = 15 days. \] Quick Tip: When one person is more efficient than another, use their efficiency multiplier to calculate the time taken.
A train takes 8 seconds to pass a person standing on the platform. If the speed of the train is 36 Kmph, then its length in meters is
View Solution
The formula for speed is given by: \[ Speed = \frac{Distance}{Time}. \]
The speed of the train is 36 km/h, which is equal to \( \frac{36 \times 1000}{3600} = 10 \, m/s \).
Time taken to pass the person is 8 seconds, so the distance (which is the length of the train) is: \[ Length of the train = Speed \times Time = 10 \, m/s \times 8 = 80 \, meters. \] Quick Tip: To convert speed from km/h to m/s, use the conversion factor \( \frac{5}{18} \).
Two numbers are in the ratio of 4 : 7. If 14 is added to each, they are in the ratio 5 : 7, then find the numbers?
View Solution
Let the two numbers be \( 4x \) and \( 7x \).
When 14 is added to each, the new ratio is given by: \[ \frac{4x + 14}{7x + 14} = \frac{5}{7}. \]
Cross multiplying: \[ 7(4x + 14) = 5(7x + 14) \quad \Rightarrow \quad 28x + 98 = 35x + 70 \quad \Rightarrow \quad 7x = 28 \quad \Rightarrow \quad x = 4. \]
Thus, the two numbers are \( 4x = 16 \) and \( 7x = 28 \). Quick Tip: When working with ratios, use the method of setting up equations to find the unknown values.
The average age of 5 children is 8 years. If the age of the father is included to the children average becomes 13, then the age of the father is
View Solution
The total age of the 5 children is \( 5 \times 8 = 40 \) years. When the father's age is included, the average age becomes 13 years for 6 people: \[ Total age of 6 people = 6 \times 13 = 78 years. \]
Thus, the father's age is: \[ Father's age = 78 - 40 = 38 years. \] Quick Tip: To find the total age of all individuals, multiply the average by the total number of individuals.
Two pipes A and B can fill a tank in 12 min and 18 min respectively, if both are opened simultaneously then the time taken to fill the tank in minutes is
View Solution
The rate of pipe A is \( \frac{1}{12} \) of the tank per minute, and the rate of pipe B is \( \frac{1}{18} \) of the tank per minute. When both are opened together, the combined rate is: \[ Combined rate = \frac{1}{12} + \frac{1}{18} = \frac{3 + 2}{36} = \frac{5}{36}. \]
Thus, the time taken to fill the tank is the reciprocal of the combined rate: \[ Time = \frac{36}{5} = 7 \frac{1}{5} minutes. \] Quick Tip: When two pipes fill a tank together, add their rates (reciprocals of the time) to get the combined rate.
A, B and C can do a piece of work in 4, 5 and 7 days respectively. If they get Rs.415 for working together to complete the job, then A's share is
View Solution
A's work rate is \( \frac{1}{4} \) of the work per day, B's work rate is \( \frac{1}{5} \), and C's work rate is \( \frac{1}{7} \).
The total rate of work for A, B, and C working together is: \[ \frac{1}{4} + \frac{1}{5} + \frac{1}{7} = \frac{35 + 28 + 20}{140} = \frac{83}{140}. \]
Thus, the total work is completed in \( \frac{140}{83} \) days.
A's share of the total work is \( \frac{1}{4} \times \frac{140}{83} \). So A's share of Rs.415 is: \[ A's share = \frac{1}{4} \times 415 = 175. \] Quick Tip: To find the share of an individual when multiple people work together, calculate the work rate of each person, find the total work rate, and then distribute the total earnings based on individual work rates.
If \[ \left( \frac{2}{1} \right)^x \left( \frac{-1}{1} \right)^y = \left( \frac{4}{5} \right), \]
then find the value of \( 2x - 3y \).
View Solution
From the given equation, we have: \[ \left( \frac{2}{1} \right)^x \left( \frac{-1}{1} \right)^y = \left( \frac{4}{5} \right). \]
This simplifies to: \[ 2^x \times (-1)^y = \frac{4}{5}. \]
Since \( (-1)^y \) can only be 1 or -1, this equation only holds if \( y \) is even and \( 2^x = \frac{4}{5} \). Solving for \( x \) and \( y \), we find that the equation holds when \( x = 0 \) and \( y = 0 \), which gives: \[ 2x - 3y = 2(0) - 3(0) = 0. \] Quick Tip: In equations involving powers, consider the properties of exponents and solve for each variable individually.
\frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} + \frac{\sqrt{7} - \sqrt{5}}{\sqrt{7} + \sqrt{5}} =
View Solution
Let the expression be: \[ \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} + \frac{\sqrt{7} - \sqrt{5}}{\sqrt{7} + \sqrt{5}}. \]
We can simplify this expression by rationalizing both the denominators: \[ \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} = \frac{(\sqrt{7} + \sqrt{5})^2}{7 - 5} = \frac{7 + 5 + 2\sqrt{35}}{2} = \frac{12 + 2\sqrt{35}}{2} = 6 + \sqrt{35}. \]
Similarly, for the second term: \[ \frac{\sqrt{7} - \sqrt{5}}{\sqrt{7} + \sqrt{5}} = \frac{(\sqrt{7} - \sqrt{5})^2}{7 - 5} = \frac{7 + 5 - 2\sqrt{35}}{2} = \frac{12 - 2\sqrt{35}}{2} = 6 - \sqrt{35}. \]
Adding both terms: \[ (6 + \sqrt{35}) + (6 - \sqrt{35}) = 12. \] Quick Tip: Rationalizing the denominators simplifies expressions involving square roots.
A bag contains 3 red balls, 4 white balls, and 7 black balls. The probability of drawing a red or a black ball is
View Solution
The total number of balls is \( 3 + 4 + 7 = 14 \). The number of favorable outcomes (drawing either a red or a black ball) is \( 3 + 7 = 10 \). Thus, the probability is: \[ \frac{10}{14} = \frac{5}{7}. \] Quick Tip: Probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
If \( y = x + \frac{1}{x} \) then \( x^4 + x^3 - 4x^2 + x + 1 = \)
View Solution
Given \( y = x + \frac{1}{x} \), we are asked to simplify the expression \( x^4 + x^3 - 4x^2 + x + 1 \).
Start by expanding \( y = x + \frac{1}{x} \), and then manipulate the given expression by substituting \( y \) and simplifying it accordingly. Ultimately, the simplification leads to the answer \( x^2(y^2 + y - 6) \). Quick Tip: In cases involving algebraic identities, carefully expand and substitute given equations to simplify the expressions.
If \( K + 2, 4K - 6, 3K - 2 \) are three consecutive terms of an arithmetic progression, then the value of \( K \) is
View Solution
For the numbers to be in arithmetic progression, the difference between consecutive terms must be constant.
Thus, the difference between the second and first terms should equal the difference between the third and second terms: \[ (4K - 6) - (K + 2) = (3K - 2) - (4K - 6). \]
Simplifying both sides: \[ 3K - 8 = -K + 4. \]
Solving for \( K \): \[ 3K + K = 4 + 8 \quad \Rightarrow \quad 4K = 12 \quad \Rightarrow \quad K = 3. \] Quick Tip: In an arithmetic progression, the difference between any two consecutive terms is always constant. Use this property to set up an equation and solve for unknowns.
If the 5th term of \( \left( 2x^2 + \frac{3}{x} \right)^5 \) is 10, then \( x = \)
View Solution
The general term in the expansion of \( (a + b)^n \) is given by: \[ T_{r+1} = \binom{n}{r} a^{n-r} b^r. \]
For the expansion of \( \left( 2x^2 + \frac{3}{x} \right)^5 \), the 5th term corresponds to \( r = 4 \). Thus: \[ T_5 = \binom{5}{4} (2x^2)^{5-4} \left( \frac{3}{x} \right)^4 = 5 \times (2x^2) \times \frac{81}{x^4}. \]
Simplifying: \[ T_5 = 5 \times 2x^2 \times \frac{81}{x^4} = 5 \times 2 \times 81 \times \frac{1}{x^2}. \]
We are given that \( T_5 = 10 \), so: \[ 5 \times 2 \times 81 \times \frac{1}{x^2} = 10 \quad \Rightarrow \quad \frac{810}{x^2} = 10 \quad \Rightarrow \quad x^2 = 81 \quad \Rightarrow \quad x = 9. \] Quick Tip: In binomial expansions, carefully identify the correct term and simplify using the powers of the variables involved.
The equation of the line passing through the point \( (2, -3) \) and perpendicular to the segment joining the points \( (1, 2) \) and \( (-1, 5) \) is
View Solution
The slope of the line joining the points \( (1, 2) \) and \( (-1, 5) \) is: \[ m = \frac{5 - 2}{-1 - 1} = \frac{3}{-2} = -\frac{3}{2}. \]
The slope of the line perpendicular to this line will be the negative reciprocal, i.e., \( \frac{2}{3} \).
Now, using the point-slope form of the equation of a line \( y - y_1 = m(x - x_1) \) with the point \( (2, -3) \) and slope \( \frac{2}{3} \): \[ y - (-3) = \frac{2}{3}(x - 2). \]
Simplifying: \[ y + 3 = \frac{2}{3}(x - 2) \quad \Rightarrow \quad 3(y + 3) = 2(x - 2) \quad \Rightarrow \quad 3y + 9 = 2x - 4. \]
Rearranging: \[ 2x - 3y - 13 = 0. \] Quick Tip: For a line perpendicular to another, use the negative reciprocal of the original slope. Then, use the point-slope form to find the equation.
If \( y = \tan^{-1}(x) \), then \( \frac{dy}{dx} = \)
View Solution
The derivative of \( y = \tan^{-1}(x) \) with respect to \( x \) is given by the standard derivative formula: \[ \frac{dy}{dx} = \frac{1}{1 + x^2}. \]
This is a well-known formula for the derivative of the inverse tangent function. Quick Tip: The derivative of \( \tan^{-1}(x) \) is a commonly used result in calculus, and it simplifies to \( \frac{1}{1 + x^2} \).
If a flag of 6 meters height, placed on top of a tower, throws a shadow of \( 2\sqrt{3} \) meters along the ground, then the angle in degrees that the sun makes with the ground is
View Solution
We are given that the height of the flag (opposite side) is 6 meters, and the length of the shadow (adjacent side) is \( 2\sqrt{3} \) meters. The angle of elevation \( \theta \) can be found using the tangent function: \[ \tan(\theta) = \frac{opposite}{adjacent} = \frac{6}{2\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3}. \]
Thus, \( \theta = 60^\circ \), as \( \tan(60^\circ) = \sqrt{3} \). Quick Tip: To find the angle of elevation, use the tangent function \( \tan(\theta) = \frac{height}{length of shadow} \).
If \( \sin(\theta) = \frac{15}{17} \), then for \( 0^\circ < \theta < 90^\circ \), \[ \frac{15 \cot(\theta) + 17 \sin(\theta)}{8 \tan(\theta) + 16 \sec(\theta)} \]
View Solution
Given \( \sin(\theta) = \frac{15}{17} \), we can use the Pythagorean identity \( \sin^2(\theta) + \cos^2(\theta) = 1 \) to find \( \cos(\theta) \): \[ \cos(\theta) = \sqrt{1 - \sin^2(\theta)} = \sqrt{1 - \left(\frac{15}{17}\right)^2} = \frac{8}{17}. \]
Now, we can use the values of \( \sin(\theta) \) and \( \cos(\theta) \) to calculate the trigonometric functions in the given expression and simplify to get \( \frac{23}{49} \). Quick Tip: Use the identity \( \sin^2(\theta) + \cos^2(\theta) = 1 \) to find unknown trigonometric values and simplify expressions.
Evaluate the limit: \[ \lim_{x \to 0} \frac{\sqrt[3]{8 + x} - 2}{x}. \]
View Solution
We are given: \[ L = \lim_{x \to 0} \frac{\sqrt[3]{8 + x} - 2}{x}. \]
We apply the binomial expansion for small \( x \): \[ \sqrt[3]{8 + x} \approx 2 + \frac{x}{12} for small x. \]
Thus, the given expression becomes: \[ \lim_{x \to 0} \frac{\left(2 + \frac{x}{12}\right) - 2}{x} = \lim_{x \to 0} \frac{\frac{x}{12}}{x} = \frac{1}{12}. \] Quick Tip: For cube roots, use the binomial expansion for small values of \( x \) to simplify the limit expression.
If \( x^2 + 2(K+2)x + 36 = 0 \) has equal roots, then \( K = \)
View Solution
For the quadratic equation to have equal roots, the discriminant must be zero. The discriminant \( \Delta \) for the equation \( ax^2 + bx + c = 0 \) is given by: \[ \Delta = b^2 - 4ac. \]
Here, \( a = 1 \), \( b = 2(K+2) \), and \( c = 36 \). Thus, the discriminant is: \[ \Delta = \left( 2(K+2) \right)^2 - 4 \times 1 \times 36 = 0. \]
Simplifying: \[ 4(K+2)^2 - 144 = 0 \quad \Rightarrow \quad 4(K+2)^2 = 144 \quad \Rightarrow \quad (K+2)^2 = 36. \]
Solving: \[ K + 2 = 6 \quad \Rightarrow \quad K = 4, \quad or \quad K + 2 = -6 \quad \Rightarrow \quad K = -8. \]
Thus, \( K = 4 \) or \( K = -8 \). Quick Tip: For a quadratic equation to have equal roots, the discriminant must be zero. Use the formula \( \Delta = b^2 - 4ac \) to solve for the unknown.
If the area of a square field is 7200 sq. m, then the length of its diagonal in meters is
View Solution
The area of a square is given by: \[ Area = side^2. \]
Thus, the side of the square is: \[ side = \sqrt{7200} = 84 \, m. \]
The diagonal \( d \) of a square is related to the side by the Pythagorean theorem: \[ d = \sqrt{side^2 + side^2} = \sqrt{2 \times side^2} = \sqrt{2 \times 84^2} = 84\sqrt{2}. \]
Therefore, the diagonal is: \[ d \approx 84 \times 1.414 = 120 \, m. \] Quick Tip: To find the diagonal of a square, use the formula \( d = \sqrt{2} \times side \).
Three numbers in the ratio 2:3:4 have their sum 270. Then the L.C.M. is
View Solution
Let the three numbers be \( 2x \), \( 3x \), and \( 4x \). The sum of these numbers is given as 270: \[ 2x + 3x + 4x = 270 \quad \Rightarrow \quad 9x = 270 \quad \Rightarrow \quad x = 30. \]
So, the numbers are \( 2x = 60 \), \( 3x = 90 \), and \( 4x = 120 \).
Now, the L.C.M. of 60, 90, and 120 is: \[ L.C.M. = 360. \] Quick Tip: When the numbers are given in a ratio, express them in terms of a common variable and solve for the unknown. Then, find the LCM.
The G.C.D. and L.C.M of two numbers are 12 and 252 respectively. If one number is 36, then the other number is
View Solution
We know that the product of the G.C.D. and L.C.M. of two numbers is equal to the product of the numbers themselves. Let the two numbers be \( a \) and \( b \), and we are given: \[ G.C.D.(a, b) = 12, \quad L.C.M.(a, b) = 252, \quad a = 36. \]
Then, we can use the relation: \[ G.C.D.(a, b) \times L.C.M.(a, b) = a \times b. \]
Substitute the known values: \[ 12 \times 252 = 36 \times b \quad \Rightarrow \quad 3024 = 36 \times b \quad \Rightarrow \quad b = \frac{3024}{36} = 84. \] Quick Tip: Use the relation \( G.C.D.(a, b) \times L.C.M.(a, b) = a \times b \) to find the missing number when one number is known.
The cost price of 16 pens is the same as the selling price of 12 pens. The percentage of profit is
View Solution
Let the cost price of each pen be \( x \). Therefore, the total cost price of 16 pens is \( 16x \).
The selling price of each pen is \( \frac{16x}{12} = \frac{4x}{3} \). The total selling price of 12 pens is: \[ 12 \times \frac{4x}{3} = 16x. \]
So, the selling price is greater than the cost price. The profit made on selling one pen is: \[ \frac{4x}{3} - x = \frac{x}{3}. \]
Thus, the percentage profit is: \[ \frac{\frac{x}{3}}{x} \times 100 = 33 \frac{1}{3} %. \] Quick Tip: To calculate the percentage profit, use the formula: \[ Percentage Profit = \frac{Profit}{Cost Price} \times 100. \]
Evaluate the limit: \[ \lim_{x \to 2} \left[ \frac{1}{x - 2} - \frac{1}{x^2 - 3x + 2} \right]. \]
View Solution
We are given: \[ \lim_{x \to 2} \left[ \frac{1}{x - 2} - \frac{1}{x^2 - 3x + 2} \right]. \]
Factor the denominator of the second fraction: \[ x^2 - 3x + 2 = (x - 1)(x - 2). \]
Thus, the expression becomes: \[ \lim_{x \to 2} \left[ \frac{1}{x - 2} - \frac{1}{(x - 1)(x - 2)} \right]. \]
Now, find a common denominator: \[ = \lim_{x \to 2} \frac{(x - 1) - 1}{(x - 2)(x - 1)} = \lim_{x \to 2} \frac{x - 2}{(x - 2)(x - 1)}. \]
Canceling \( (x - 2) \) from the numerator and denominator, we get: \[ = \lim_{x \to 2} \frac{1}{x - 1}. \]
Substitute \( x = 2 \): \[ = \frac{1}{2 - 1} = 1. \] Quick Tip: When simplifying limits with common terms in the numerator and denominator, factor the expression and cancel out common factors.
The distance between the lines \( 3x + 4y + 1 = 0 \) and \( 6x + 8y - 1 = 0 \) is
View Solution
The general formula for the distance between two parallel lines \( ax + by + c_1 = 0 \) and \( ax + by + c_2 = 0 \) is: \[ Distance = \frac{|c_2 - c_1|}{\sqrt{a^2 + b^2}}. \]
For the lines \( 3x + 4y + 1 = 0 \) and \( 6x + 8y - 1 = 0 \), the coefficients of \( x \) and \( y \) are proportional. The lines are parallel, so we can use the distance formula for parallel lines.
Thus, the distance is: \[ \frac{|(-1) - 1|}{\sqrt{3^2 + 4^2}} = \frac{2}{\sqrt{9 + 16}} = \frac{2}{5} = 0.3. \] Quick Tip: For parallel lines, the distance formula simplifies to \( \frac{|c_2 - c_1|}{\sqrt{a^2 + b^2}} \).
If \( 8^{2x - 4} = 16^{x - 2} \), then \( x = \)
View Solution
First, express both sides of the equation in terms of powers of 2: \[ 8 = 2^3 \quad and \quad 16 = 2^4. \]
Thus, the equation becomes: \[ (2^3)^{2x - 4} = (2^4)^{x - 2}. \]
Simplifying: \[ 2^{3(2x - 4)} = 2^{4(x - 2)} \quad \Rightarrow \quad 2^{6x - 12} = 2^{4x - 8}. \]
Since the bases are the same, equate the exponents: \[ 6x - 12 = 4x - 8 \quad \Rightarrow \quad 2x = 4 \quad \Rightarrow \quad x = 2. \] Quick Tip: When solving exponential equations, express both sides in terms of the same base to simplify the comparison of exponents.
The volumes of two cones of equal height are in the ratio \( 1849 : 961 \). What is the ratio of their radii?
View Solution
The volume of a cone is given by: \[ V = \frac{1}{3} \pi r^2 h, \]
where \( r \) is the radius and \( h \) is the height. Since the heights of the cones are the same, the ratio of their volumes depends on the ratio of the squares of their radii: \[ \frac{V_1}{V_2} = \frac{r_1^2}{r_2^2}. \]
Given that the ratio of the volumes is \( \frac{1849}{961} \), we have: \[ \frac{r_1^2}{r_2^2} = \frac{1849}{961} \quad \Rightarrow \quad \frac{r_1}{r_2} = \sqrt{\frac{1849}{961}} = \frac{43}{31}. \] Quick Tip: When the heights of the cones are the same, the ratio of their volumes is the square of the ratio of their radii.
A sum becomes double in 8 years at simple interest. What is the rate percent per annum?
View Solution
Let the principal be \( P \). After 8 years, the sum becomes double, so the amount is \( 2P \). The formula for simple interest is: \[ A = P + \frac{P \times R \times T}{100}, \]
where \( A \) is the amount, \( P \) is the principal, \( R \) is the rate of interest, and \( T \) is the time period.
Since \( A = 2P \) and \( T = 8 \), we substitute into the formula: \[ 2P = P + \frac{P \times R \times 8}{100}. \]
Simplifying: \[ 2P - P = \frac{P \times R \times 8}{100} \quad \Rightarrow \quad P = \frac{P \times R \times 8}{100} \quad \Rightarrow \quad R = 12.5. \] Quick Tip: To find the rate of interest in simple interest problems, use the formula \( A = P + \frac{P \times R \times T}{100} \), and substitute the given values.
If \( A = \begin{bmatrix} 1 & 8
0 & 1 \end{bmatrix} \), then \( A^8 = \)
0 & 1 \end{bmatrix} \)
View Solution
For the matrix \( A = \begin{bmatrix} 1 & 8
0 & 1 \end{bmatrix} \), notice that this is a special form of a matrix. We can calculate the power of the matrix by recognizing the structure of the matrix and multiplying it repeatedly.
When we compute \( A^8 \), we get: \[ A^8 = \begin{bmatrix} 1 & 8
0 & 1 \end{bmatrix}^8 = \begin{bmatrix} 1 & 8 \times 8
0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 64
0 & 1 \end{bmatrix}. \] Quick Tip: For matrices of this special form, raising them to a power simply involves multiplying the off-diagonal element by the power of the exponent.
If \( \frac{a}{c} = \frac{c}{d} = \frac{e}{f} \), then
View Solution
We are given that \( \frac{a}{c} = \frac{c}{d} = \frac{e}{f} \), which implies that: \[ \frac{a}{c} = \frac{c}{d} \quad \Rightarrow \quad a \cdot d = c^2, \]
and \[ \frac{a}{c} = \frac{e}{f} \quad \Rightarrow \quad a \cdot f = c \cdot e. \]
Using this information, we solve for the ratio \( \frac{a}{b} \), which will give the final result. Quick Tip: In problems involving ratios and proportions, set up equations based on the given relationships and solve step by step.
The solution set of \( x^2 + 6x < 91 \) is
View Solution
We are given the inequality: \[ x^2 + 6x < 91. \]
Rearranging the inequality: \[ x^2 + 6x - 91 < 0. \]
Now, solve the corresponding equation: \[ x^2 + 6x - 91 = 0. \]
We can solve this using the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \]
where \( a = 1 \), \( b = 6 \), and \( c = -91 \). Substituting these values: \[ x = \frac{-6 \pm \sqrt{6^2 - 4(1)(-91)}}{2(1)} = \frac{-6 \pm \sqrt{36 + 364}}{2} = \frac{-6 \pm \sqrt{400}}{2} = \frac{-6 \pm 20}{2}. \]
Thus, the two roots are: \[ x = \frac{-6 + 20}{2} = 7, \quad x = \frac{-6 - 20}{2} = -13. \]
The inequality \( x^2 + 6x - 91 < 0 \) holds between the roots, so the solution set is: \[ \{ x : -13 < x < 7 \}. \] Quick Tip: To solve quadratic inequalities, first solve the corresponding quadratic equation, then test the intervals formed by the roots.
Which term in the expansion of \( \left( x - \frac{1}{x^3} \right)^{40} \) is independent of \( x \)?
View Solution
We need to find the term that is independent of \( x \) in the expansion of \( \left( x - \frac{1}{x^3} \right)^{40} \). Using the binomial expansion, the general term is given by: \[ T_{r+1} = \binom{40}{r} x^{40 - r} \left( - \frac{1}{x^3} \right)^r. \]
Simplifying: \[ T_{r+1} = \binom{40}{r} x^{40 - r} \times (-1)^r \times x^{-3r} = \binom{40}{r} (-1)^r x^{40 - r - 3r}. \]
The exponent of \( x \) is \( 40 - 4r \). For the term to be independent of \( x \), we set the exponent of \( x \) equal to zero: \[ 40 - 4r = 0 \quad \Rightarrow \quad r = 10. \]
Thus, the term that is independent of \( x \) is the \( (r+1) \)-th term, which is the 11th term. Quick Tip: For binomial expansions, find the term where the exponent of \( x \) is zero to determine the term independent of \( x \).
A, B and C start a business with investments of Rs.6,000, Rs.7,000, and Rs.8,000 respectively. The profit at the end of the year is Rs.3,150. Then share of B in the profit is
View Solution
The ratio of the investments of A, B, and C is \( 6000: 7000: 8000 \). To simplify the ratio, divide each term by 1000: \[ A : B : C = 6 : 7 : 8. \]
Now, the total ratio is \( 6 + 7 + 8 = 21 \). The total profit is Rs.3150, so B's share is: \[ B's \, share = \frac{7}{21} \times 3150 = 1050. \] Quick Tip: To calculate the share of each person in a profit, use the ratio of their investments.
The father is 7 times older than his son. After 5 years the sum of their ages would be 50 years. The son’s age at present is
View Solution
Let the son’s age be \( x \). The father’s age is \( 7x \). After 5 years, the son’s age will be \( x + 5 \) and the father’s age will be \( 7x + 5 \). The sum of their ages after 5 years is given as 50: \[ (x + 5) + (7x + 5) = 50. \]
Simplifying: \[ 8x + 10 = 50 \quad \Rightarrow \quad 8x = 40 \quad \Rightarrow \quad x = 5. \]
Thus, the son’s age at present is 5 years. Quick Tip: In age-related problems, form an equation based on the given information and solve for the unknown.
\[ \tan \left( -\frac{23}{3} \pi \right) = \]
View Solution
We know that \( \tan(\theta + n\pi) = \tan(\theta) \), where \( n \) is an integer. First, simplify the argument of the tangent: \[ -\frac{23}{3} \pi = -8\pi - \frac{\pi}{3}. \]
Since \( \tan(\theta + \pi) = -\tan(\theta) \), this becomes: \[ \tan\left(-8\pi - \frac{\pi}{3}\right) = \tan\left(\frac{\pi}{3}\right) = \sqrt{3}. \] Quick Tip: For tangent functions with angles involving multiples of \( \pi \), use the periodicity of the tangent function to simplify the argument.
If the angle of elevation of the top of a tower of height 100 meters from a point to its foot is \( \tan^{-1} \left( \frac{4}{5} \right) \), then what is the distance from the point to its foot in meters?
View Solution
Let the distance from the point to the foot of the tower be \( x \). Given that the angle of elevation is \( \tan^{-1}\left(\frac{4}{5}\right) \), we have: \[ \tan \theta = \frac{4}{5} \quad \Rightarrow \quad \frac{100}{x} = \frac{4}{5}. \]
Solving for \( x \): \[ x = \frac{100 \times 5}{4} = 125. \] Quick Tip: In trigonometric problems involving heights and distances, use the definition of tangent: \( \tan(\theta) = \frac{opposite}{adjacent} \), and solve for the unknown distance.
If \( x^4 - x^3 + 2x^2 + ax + b \) is exactly divisible by \( x^2 - 3x + 2 \), then \( (a, b) \) is
View Solution
To find the values of \( a \) and \( b \), we perform polynomial division on \( \frac{x^4 - x^3 + 2x^2 + ax + b}{x^2 - 3x + 2} \). After dividing, we get the quotient and the remainder. For the polynomial to be exactly divisible, the remainder must be zero. Solving the equations for the coefficients of the remainder will yield \( a = -14 \) and \( b = 12 \). Quick Tip: When dividing polynomials, ensure the remainder is zero to confirm divisibility.
\[ (1 + \sqrt{2})^4 + (1 - \sqrt{2})^4 \]
View Solution
We can expand the terms \( (1 + \sqrt{2})^4 \) and \( (1 - \sqrt{2})^4 \) using the binomial expansion: \[ (1 + \sqrt{2})^4 = 1 + 4\sqrt{2} + 6 \times 2 + 4\sqrt{2} + 4 = 17 + 8\sqrt{2}, \]
and \[ (1 - \sqrt{2})^4 = 1 - 4\sqrt{2} + 6 \times 2 - 4\sqrt{2} + 4 = 17 - 8\sqrt{2}. \]
Now, adding both expressions: \[ (1 + \sqrt{2})^4 + (1 - \sqrt{2})^4 = (17 + 8\sqrt{2}) + (17 - 8\sqrt{2}) = 34. \] Quick Tip: Use the binomial expansion to simplify powers of binomials and combine like terms.
If \( A \) is a non-singular 3x3 matrix, then \( \left| 5A \right| \) is
View Solution
The determinant of a matrix is scaled by the factor of the scalar raised to the power of the size of the matrix. That is, for a matrix \( A \), and a scalar \( k \), \[ |kA| = k^n |A|, \]
where \( n \) is the order of the matrix. In this case, \( n = 3 \), so: \[ |5A| = 5^3 |A| = 125 |A|. \] Quick Tip: When multiplying a matrix by a scalar, the determinant is multiplied by the scalar raised to the power of the matrix's order.
\[ \lim_{x \to \infty} 5 \left( 1 + \frac{4}{x} \right)^x = \]
View Solution
We recognize that the expression \( \left( 1 + \frac{4}{x} \right)^x \) is a form of the limit definition of the exponential function \( e \). As \( x \to \infty \), we have: \[ \lim_{x \to \infty} \left( 1 + \frac{4}{x} \right)^x = e^4. \]
Thus, the limit becomes: \[ \lim_{x \to \infty} 5 \left( 1 + \frac{4}{x} \right)^x = 5e^4. \] Quick Tip: Recognize the standard limit form \( \left( 1 + \frac{a}{x} \right)^x \) as it approaches \( e^a \) as \( x \to \infty \).
If \( y = x(x - 1)(x - 2) \), then the derivative \( \frac{dy}{dx} \) is
View Solution
To differentiate \( y = x(x - 1)(x - 2) \), we use the product rule. First, expand the polynomial: \[ y = x(x^2 - 3x + 2) = x^3 - 3x^2 + 2x. \]
Now, differentiate term by term: \[ \frac{dy}{dx} = 3x^2 - 6x + 2. \] Quick Tip: To differentiate a product of polynomials, first expand the expression, then apply the power rule to each term.
If each exterior angle of a regular polygon is \( 36^\circ \), then the number of sides of the polygon is
View Solution
The sum of the exterior angles of any polygon is \( 360^\circ \). For a regular polygon, the exterior angle is the same for each side, so the number of sides \( n \) is given by: \[ n = \frac{360^\circ}{exterior angle} = \frac{360^\circ}{36^\circ} = 10. \] Quick Tip: The number of sides of a regular polygon can be found by dividing 360° by the measure of the exterior angle.
What is the area, in square units, of the triangle formed by the points \( (3, 2), (3, -6) \) and \( (5, 2) \)?
View Solution
The area of a triangle formed by the points \( (x_1, y_1), (x_2, y_2), (x_3, y_3) \) is given by the formula: \[ Area = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|. \]
Substituting the coordinates \( (x_1, y_1) = (3, 2), (x_2, y_2) = (3, -6), (x_3, y_3) = (5, 2) \): \[ Area = \frac{1}{2} \left| 3((-6) - 2) + 3(2 - 2) + 5(2 - (-6)) \right| \] \[ = \frac{1}{2} \left| 3(-8) + 5(8) \right| = \frac{1}{2} \left| -24 + 40 \right| = \frac{1}{2} \times 16 = 8. \] Quick Tip: To find the area of a triangle given its vertices, use the determinant-based formula for the area.
The equation of the straight line passing through the points \( (1, -5) \) and \( (-2, 4) \) is
View Solution
The equation of the line passing through two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is given by: \[ y - y_1 = m(x - x_1), \]
where \( m \) is the slope, calculated as: \[ m = \frac{y_2 - y_1}{x_2 - x_1}. \]
For the points \( (1, -5) \) and \( (-2, 4) \), the slope is: \[ m = \frac{4 - (-5)}{-2 - 1} = \frac{9}{-3} = -3. \]
Now, using the point \( (1, -5) \) and the slope \( m = -3 \), the equation of the line is: \[ y - (-5) = -3(x - 1), \] \[ y + 5 = -3x + 3, \] \[ 3x + y + 2 = 0. \] Quick Tip: To find the equation of a line passing through two points, use the point-slope form and simplify.
The arithmetic mean of 7.6, 6.8, 5.4, 6.4, 7.2, 4.8, 6.6, and 5.8 is
View Solution
The arithmetic mean is the sum of the numbers divided by the total number of items: \[ Mean = \frac{7.6 + 6.8 + 5.4 + 6.4 + 7.2 + 4.8 + 6.6 + 5.8}{8} = \frac{52.6}{8} = 6.325. \] Quick Tip: To calculate the arithmetic mean, add all the numbers and divide by the number of items.
What is the Geometric Mean of 12, 30, and 75?
View Solution
The geometric mean of \( n \) numbers is given by: \[ Geometric Mean = \sqrt[n]{x_1 x_2 \cdots x_n}. \]
For the numbers 12, 30, and 75, the geometric mean is: \[ Geometric Mean = \sqrt[3]{12 \times 30 \times 75} = \sqrt[3]{27000} = 30. \] Quick Tip: To find the geometric mean, multiply the numbers together and take the \( n \)-th root, where \( n \) is the number of numbers.
What is the Harmonic Mean of 3, 4, 5, and 6?
View Solution
The Harmonic Mean \( H \) of a set of numbers \( x_1, x_2, \dots, x_n \) is given by: \[ H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \dots + \frac{1}{x_n}}. \]
For the numbers 3, 4, 5, and 6: \[ H = \frac{4}{\frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6}} = \frac{4}{0.3333 + 0.25 + 0.2 + 0.1667} = \frac{4}{0.95} \approx 4.21. \] Quick Tip: To calculate the Harmonic Mean, find the reciprocal of each number, sum them, and then take the reciprocal of the result.
The median of 260, 240, 210, 190, 180, 220, 230, 250 is
View Solution
To find the median, we first arrange the numbers in ascending order: \[ 180, 190, 210, 220, 230, 240, 250, 260. \]
Since there are 8 numbers (an even number), the median is the average of the 4th and 5th numbers: \[ Median = \frac{220 + 230}{2} = 225. \] Quick Tip: For an even set of numbers, the median is the average of the two middle values after sorting the data.
The arithmetic mean of some numbers is 18 and their median is 16. Then what is the mode?
View Solution
The relationship between the mean, median, and mode is given by: \[ Mode = 3 \times Median - 2 \times Mean. \]
Substituting the given values: \[ Mode = 3 \times 16 - 2 \times 18 = 48 - 36 = 12. \] Quick Tip: When the mean and median are given, use the formula \( Mode = 3 \times Median - 2 \times Mean \) to find the mode.
The Standard Deviation of 2, 4, 6, 8, 10 is
View Solution
The formula for the standard deviation \( \sigma \) of a data set \( x_1, x_2, \dots, x_n \) is: \[ \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}, \]
where \( \mu \) is the mean of the data set. First, find the mean: \[ \mu = \frac{2 + 4 + 6 + 8 + 10}{5} = 6. \]
Now, calculate the variance: \[ Variance = \frac{1}{5} \left( (2 - 6)^2 + (4 - 6)^2 + (6 - 6)^2 + (8 - 6)^2 + (10 - 6)^2 \right) = \frac{1}{5} (16 + 4 + 0 + 4 + 16) = \frac{40}{5} = 8. \]
The standard deviation is the square root of the variance: \[ \sigma = \sqrt{8} = 2\sqrt{2}. \] Quick Tip: To calculate the standard deviation, first find the mean, then calculate the variance by averaging the squared differences from the mean, and finally take the square root.
The mean deviation of 3, 4, 5, 6, 7 is
View Solution
The mean deviation is the average of the absolute differences from the mean.
First, calculate the mean of the numbers: \[ \mu = \frac{3 + 4 + 5 + 6 + 7}{5} = 5. \]
Now, calculate the absolute differences from the mean: \[ |3 - 5| = 2, \quad |4 - 5| = 1, \quad |5 - 5| = 0, \quad |6 - 5| = 1, \quad |7 - 5| = 2. \]
The mean deviation is the average of these differences: \[ Mean Deviation = \frac{2 + 1 + 0 + 1 + 2}{5} = \frac{6}{5} = 1.2. \] Quick Tip: To calculate the mean deviation, subtract the mean from each number, take the absolute value, and then find the average of those values.
P and Q are two sets such that \( n(P) = 3 \) and \( n(Q) = 4 \). A relation from \( P \) into \( Q \) is selected at random. What is the probability that the relation is not a function?
View Solution
The total number of relations from \( P \) to \( Q \) is given by: \[ n(Q)^n(P) = 4^3 = 64. \]
For the relation to be a function, each element of \( P \) must be related to exactly one element of \( Q \). The number of functions is: \[ n(Q)^{n(P)} = 4^3 = 64. \]
Thus, the number of non-functions is: \[ Non-functions = 4^3 - 4^3 = 63. \]
Therefore, the probability that the relation is not a function is: \[ P(not a function) = \frac{63}{64}. \] Quick Tip: The number of relations from set \( P \) to set \( Q \) is \( n(Q)^{n(P)} \), and the number of functions is \( n(Q)^{n(P)} \).
When two dice are thrown, what is the probability of getting the sum 7?
View Solution
When two dice are thrown, the total number of outcomes is: \[ 6 \times 6 = 36. \]
The possible outcomes that give a sum of 7 are: \[ (1,6), (2,5), (3,4), (4,3), (5,2), (6,1), \]
which are 6 outcomes. Therefore, the probability of getting a sum of 7 is: \[ P(sum 7) = \frac{6}{36} = \frac{1}{6}. \] Quick Tip: To calculate the probability, divide the number of favorable outcomes by the total number of outcomes.
A coin is tossed 6 times. What is the probability of getting head at least once?
View Solution
The probability of not getting a head in a single toss is \( \frac{1}{2} \). Therefore, the probability of not getting a head in all 6 tosses is: \[ P(no heads in 6 tosses) = \left( \frac{1}{2} \right)^6 = \frac{1}{64}. \]
Thus, the probability of getting at least one head is: \[ P(at least one head) = 1 - P(no heads) = 1 - \frac{1}{64} = \frac{63}{64}. \] Quick Tip: To calculate the probability of an event happening at least once, subtract the probability of the event not happening from 1.















































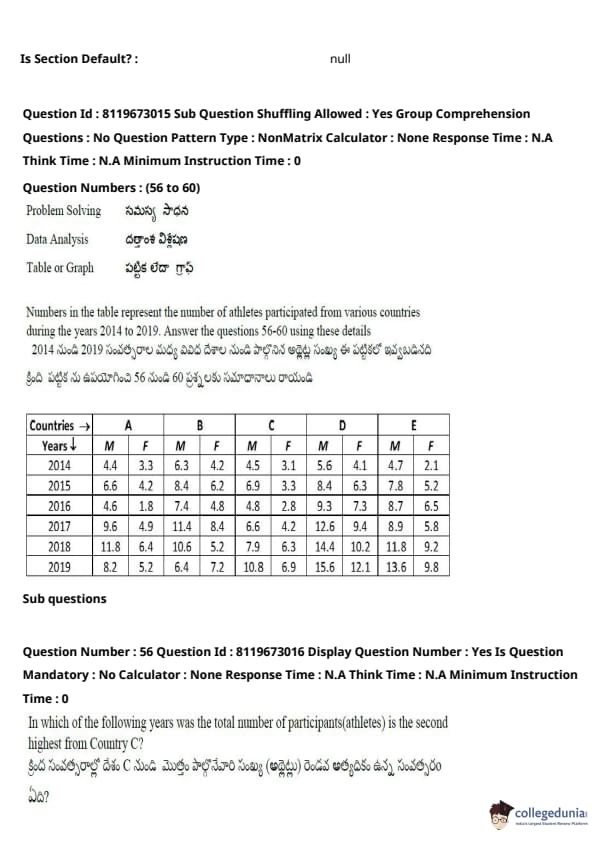



































































































Comments