NPAT 2021 Question paper with answer key pdf conducted on June 27, 2021 is available for download. The exam was successfully organized by Narsee Monjee Institute for Management Studies (NMIMS). The question paper comprised a total of 120 questions.
NPAT 2021 Question Paper with Answer Key PDFs
| NPAT 2021 Question Paper with Answer Key | Download PDF | Check Solution |
In the given sentence, four words/phrases have been underlined and the underlined words/phrases are given as options. Select the option that contains an error.
Scientists in India have developed the new variety of brinjal
View Solution
The error lies in the phrase "\underline{the new variety". The correct sentence should be "Scientists in India have developed new varieties of brinjal" (without "the" before "new variety"). The phrase should not use an article "the" when referring to general instances.
Quick Tip: When identifying errors in sentences, pay attention to the correct usage of articles ("the", "a", "an") and their placement in the sentence.
Parts of the given sentence have been underlined and given as options. One of them contains a grammatical error. Select the option that has the error.
Over the last year I have avoided to go to the doctor unless absolutely necessary
View Solution
The error lies in the phrase "\underline{to go to the doctor." The correct structure should be "I have avoided going to the doctor" as the verb "avoided" should be followed by the gerund form "going" rather than the infinitive "to go." Quick Tip: When using verbs like "avoid," "enjoy," and "consider," they should be followed by the gerund (-ing form) rather than the infinitive.
Parts of the given sentence have been underlined and given as options. One of them contains a grammatical error. Select the option that has the error.
Since the car is new, it isn’t as sturdy as my old car.
View Solution
The error lies in the phrase "\underline{it isn’t". The correct sentence should be "Since the car is new, it isn’t as sturdy \underline{as my old car." The issue is that the verb phrase "isn't" should not be used with "as" in this context. The correct construction is: "it is not as sturdy as." Quick Tip: When making comparisons with "as" and "sturdy," ensure the verb follows the correct structure for comparisons.
In the given sentence, four words/phrases have been underlined and the underlined words/phrases are given as options. Select the option that contains an error.
Ravi and Shashi is responsible for the confusion created yesterday.
View Solution
The error lies in the phrase "\underline{is responsible". Since "Ravi and Shashi" is a plural subject, the correct form of the verb should be "are responsible" instead of "is responsible." The correct sentence should be: "Ravi and Shashi are responsible for the confusion created yesterday." Quick Tip: When the subject is plural, ensure that the verb agrees with the subject in terms of number.
In the given sentence, four words/phrases have been underlined and the underlined words/phrases are given as options. Select the option that contains an error.
I have so much luggages I’m sure I’ll have to pay for excess baggage.
View Solution
The error lies in the phrase "\underline{so much luggages." The word "luggage" is uncountable, so it should not be used with "much" in the plural form. The correct sentence should be: "I have so much luggage." Quick Tip: When using uncountable nouns like "luggage," do not add the plural form.
Select the most appropriate option to fill in the blank.
Do you really think the medicine will cure you ...... your illness?
View Solution
The correct preposition to use with "cure" is "of" when referring to an illness. The sentence should read: "Do you really think the medicine will cure you \underline{of your illness?" Quick Tip: When using the verb "cure," remember that it is typically followed by "of" when referring to an illness.
Select the most appropriate option to fill in the blank.
I had the room painted. So, please don’t lean ....... the walls.
View Solution
The correct preposition here is "against." The sentence should read: "I had the room painted. So, please don’t lean \underline{against the walls." This is because "lean against" is a common phrase used when referring to resting something or someone on a vertical surface. Quick Tip: When using verbs like "lean," "sit," or "rest," they are commonly followed by "against" when referring to a vertical surface.
Select the most appropriate option to fill in the blank.
By the time you reach the site, the electricians ...... the lights in the bedroom.
View Solution
The correct answer is "will have fixed." This is an example of the future perfect tense, which is used to indicate that an action will be completed before another point in the future. The sentence should read: "By the time you reach the site, the electricians \underline{will have fixed the lights in the bedroom." Quick Tip: Use the future perfect tense ("will have + past participle") to indicate that an action will be completed by a specific time in the future.
Select the most appropriate option to fill in the blank.
They ...... their hometown twice a year.
View Solution
The correct answer is "visit." The sentence is referring to a regular or habitual action, which is best expressed in the simple present tense. The correct sentence should be: "They \underline{visit their hometown twice a year." Quick Tip: For habitual actions, use the simple present tense.
Select the most appropriate option to fill in the blank.
Tawang is a beautiful place to visit ..... the difficulties faced while getting there.
View Solution
The correct answer is "despite." The sentence requires a preposition that introduces a contrast between the beauty of the place and the difficulties in getting there. "Despite" is used to show contrast, making the correct sentence: "Tawang is a beautiful place to visit \underline{despite the difficulties faced while getting there." Quick Tip: Use "despite" to express contrast, particularly when something is true in spite of something else.
Select the most appropriate option to fill in the blank.
Vinu exercises regularly, ...... he is fit.
View Solution
The correct answer is "therefore." "Therefore" is used to indicate a conclusion drawn from a fact. The sentence suggests that Vinu's regular exercise leads to his fitness. Thus, "Vinu exercises regularly, \underline{therefore he is fit" is the correct construction. Quick Tip: Use "therefore" to show a logical conclusion resulting from a preceding statement.
Select the most appropriate option to fill in the blank.
Shamim invited ..... friends over to her house for dinner.
View Solution
The correct answer is "a few." "A few" is used with countable nouns to indicate a small number, while "few" without the article has a more negative connotation, meaning "not many." The sentence should read: "Shamim invited \underline{a few friends over to her house for dinner." Quick Tip: Use "a few" to indicate a small, but positive, number of countable items.
Select the most appropriate option to fill in the blank.
Shekhar finished his work quickly because he had ..... to do.
View Solution
The correct answer is "little." "Little" is used with uncountable nouns to indicate a small amount. Since "work" is uncountable, the correct sentence should be: "Shekhar finished his work quickly because he had \underline{little to do." Quick Tip: Use "little" for uncountable nouns to indicate a small quantity or amount.
Select the option that gives the most appropriate meaning of the underlined word.
I felt rather fragile for a few days after the operation.
View Solution
The correct answer is "weak." The word "fragile" refers to being physically weak or vulnerable, especially in the context of health or condition after an operation. Therefore, the sentence means that the person felt physically weak for a few days. Quick Tip: "Fragile" refers to something that is easily damaged or physically weak.
Select the option that gives the most appropriate meaning of the underlined word.
White blood cells help defend the body against infection.
View Solution
The correct answer is "protect." "Defend" means to protect something from harm or danger, and in this context, it refers to the role of white blood cells in protecting the body from infection. Quick Tip: "Defend" means to protect or safeguard from harm, particularly in a physical or metaphorical sense.
Select the option that gives the most appropriate meaning of the underlined phrase.
Now that our exams are over, let’s paint the town red.
View Solution
The correct answer is "Go out and enjoy oneself." The phrase "paint the town red" is an idiomatic expression that means to go out and have a good time, often in a celebratory manner. Quick Tip: When you encounter idiomatic phrases, remember that their meaning often differs from the literal meaning of the words used.
Select the option that gives the most appropriate meaning of the underlined phrase.
Covid-19 is a blessing in disguise. I’ve got the time to pursue my hobbies.
View Solution
The correct answer is "Something that seems unlucky at first but leads to something good later." The phrase "blessing in disguise" refers to a situation that initially appears bad or unlucky but results in something positive or beneficial. Quick Tip: When you encounter idioms, remember that they may have meanings different from the literal interpretation of the words.
Select the option that gives the most appropriate meaning of the underlined word.
My brother gets a handsome salary.
View Solution
The correct answer is "Large." The word "handsome" in this context means large or substantial, especially in terms of salary. "Handsome" can be used to describe something that is generous or significant, such as a large salary. Quick Tip: "Handsome" can refer to something substantial, especially when describing amounts such as salaries or fees.
Select the most appropriate option to fill in the blank.
Have you ...... how much it will cost?
View Solution
The correct answer is "figured out." The phrase "figured out" means to calculate or determine something. The sentence should read: "Have you \underline{figured out how much it will cost?" Quick Tip: Use "figured out" when referring to the process of determining or calculating something.
Select the most appropriate option to fill in the blank.
If you don’t want to stay at home tonight, that is ....... fine by me.
View Solution
The correct answer is "perfectly." The phrase "perfectly fine" is commonly used to mean "completely acceptable." The sentence should read: "If you don’t want to stay at home tonight, that is \underline{perfectly fine by me." Quick Tip: Use "perfectly" when emphasizing that something is completely acceptable or satisfactory.
Select the most appropriate ANTONYM of the underlined word.
The Egyptians believed that the mummified body was the home for the soul or spirit.
View Solution
The correct answer is "doubted." "Believed" means to accept something as true, and the antonym of this would be to have doubts or to question its truth. Therefore, "doubted" is the opposite of "believed." Quick Tip: When looking for antonyms, consider words that express the opposite or negation of the given term.
Sentences of a paragraph are given below in jumbled order. Arrange the sentences in the right order to form a meaningful and coherent paragraph.
A. Proper hydration means ensuring that your body maintains that level of water, as we are constantly losing water.
B. Water constitutes about 60-70 per cent of the human body.
C. In addition, it removes waste, protects our joints and keeps our skin soft and supple.
D. Hydration is important for our overall well-being irrespective of our overall activity levels.
E. It helps regulate temperature, transport nutrients and oxygen to all the millions of cells in the body.
View Solution
The correct order is DABEC. Starting with "Hydration is important" (D) sets the context for the paragraph. Then it is followed by "Water constitutes..." (A), "In addition..." (B), "It helps..." (E), and the sentence "Proper hydration..." (C) concludes it. Quick Tip: When arranging jumbled sentences, look for the sentence that introduces the main topic, and then logically link the supporting details.
Sentences of a paragraph are given below in jumbled order. Arrange the sentences in the right order to form a meaningful and coherent paragraph.
A. And woe betide anyone unlucky enough to be in the same water as a shoal of piranhas.
B. It takes only a few minutes for the vicious piranhas to reduce someone to a mere skeleton.
C. Most people think that this is a deadly creature that swarms through rivers and creeks of the Amazon rainforest looking for victims to tear apart.
D. The truth is that the piranha is really a much more nuanced animal than the mindless killer depicted in the media.
E. The piranha is a much maligned fish.
View Solution
The correct order is "ECABD." Starting with "The piranha is a much maligned fish" (E) introduces the topic, followed by the statement about the piranha being misunderstood (C). Then, it is followed by the sentence that explains the popular misconception (A), the clarification about the piranha's behavior (B), and the final clarification (D) that the piranha is more complex than it is often depicted. Quick Tip: When arranging jumbled sentences, start with the main idea and build around it logically to form a coherent paragraph.
Sentences of a paragraph are given below in jumbled order. Arrange the sentences in the right order to form a meaningful and coherent paragraph.
A. Many types of cobwebs are laced with penicillin, a fungus that contains antibiotic properties.
B. Most people associate cobwebs with an unkempt house.
C. But the presence of cobwebs does not suggest an unhealthy space.
D. In fact, quite the opposite is true.
E. This is primarily because of the dust that accumulates on the adhesive strands of cobwebs.
View Solution
The correct order is AEDBC. Starting with "Many types of cobwebs are laced with penicillin" (A) introduces the subject of the paragraph. This is followed by the explanation (E) about the dust accumulating on cobwebs, followed by (D) that counters the misconception that cobwebs are associated with unhealthy spaces. Then, (B) gives the common misconception, and (C) concludes by clarifying that cobwebs do not suggest an unhealthy environment. Quick Tip: When arranging jumbled sentences, start with the topic sentence and build around it by logically linking the supporting details.
Sentences of a paragraph are given below in jumbled order. Arrange the sentences in the right order to form a meaningful and coherent paragraph.
A. Scientists today understand that mercury is extremely poisonous and so it is used in very few products.
B. Nevertheless, there is still a significant amount of mercury in something that we eat quite regularly: fish.
C. However, in the past mercury was used in many common household objects including certain kinds of medicines.
D. Mercury is a highly toxic metal found in neon signs, fluorescent lights, and some kinds of telescopes.
E. Today, most household objects no longer contain mercury, and most people are not exposed to it at their jobs.
View Solution
The correct order is DACEB. Starting with "Mercury is a highly toxic metal" (D), this introduces mercury and its properties. Then it is followed by the sentence explaining how mercury is poisonous and rarely used today (A). The next sentence explains how mercury was used in the past (C). After that, the sentence about fish (B) adds another significant use of mercury. Finally, (E) concludes by mentioning how mercury is no longer found in many household products. Quick Tip: When arranging jumbled sentences, look for sentences that introduce the topic and follow a logical flow of information.
According to the passage, which of the following is true of the new style of working during the pandemic?
View Solution
The correct answer is "Working from bed in your nightclothes." According to the passage, many people have adopted the practice of working from bed, and how people are working in their pyjamas with coffee in hand. Quick Tip: Look for clues in the passage that refer to new habits or behaviors associated with the pandemic, such as working from bed or wearing casual attire while working.
The phrase ‘setting up shop on their mattresses’ in the second paragraph means that people started:
View Solution
The correct answer is "using their beds as office space instead of a desk." The phrase "setting up shop on their mattresses" refers to people using their beds as a space to work from, particularly during the pandemic, as described in the passage. Quick Tip: When interpreting idiomatic expressions, look for clues that point to the literal meaning of the phrase in context.
The author uses the Instagram #WorkFromBed hashtag to show how:
View Solution
The correct answer is "working from bed is gaining popularity around the world." The passage mentions that the #WorkFromBed hashtag pulls up thousands of photos, highlighting the growing trend of working from bed during the pandemic. Quick Tip: When interpreting a question about trends or social behavior, focus on how the action is described as increasing or becoming more widespread.
According to the passage, which of the following is NOT true of ‘WFB’?
View Solution
The correct answer is "Before the pandemic, Americans did not work from bed." According to the passage, a significant number of people started working from bed during the pandemic, suggesting that this was not a common practice before then. Quick Tip: Look for statements in the passage that describe changes in behavior due to specific events, like the pandemic in this case.
Which of the following sentence best captures the main idea of the passage?
View Solution
The correct answer is "People, especially youngsters, enjoy ‘WFB’ as it doesn’t need furniture and is cosy, but they are unaware of its health hazards." This option best captures the main idea of the passage, highlighting the appeal of working from bed (WFB) but also pointing out the potential health concerns. Quick Tip: When identifying the main idea of a passage, look for a sentence that covers both the positive aspects and potential drawbacks mentioned in the text.
Which of the following statement is NOT true of green, open spaces as per the passage?
View Solution
The correct answer is "Such spaces have a positive impact only on the lifespan of people." According to the passage, the presence of greenery impacts mental and physical health, not just lifespan. Therefore, this statement is not true as per the passage. Quick Tip: When answering questions about the passage, focus on understanding the impact described and whether it aligns with the provided statements.
The phrase ‘comes at a premium’ in the second paragraph refers to:
View Solution
The correct answer is "the high cost involved in access to open spaces." The phrase "comes at a premium" indicates that access to open spaces is difficult and expensive, as mentioned in the passage. Quick Tip: When a phrase like "comes at a premium" is used, it often implies scarcity and a high cost associated with it.
Raghav lives with his family in the heart of a metropolitan city. Based on your reading of the passage, he is likely to have:
View Solution
The correct answer is "no access to parks and gardens." The passage mentions that in many cities, outdoor space is scarce, and access to parks and gardens is a challenge for people living in certain areas. Quick Tip: When interpreting a question about access to resources in a city, focus on how the passage describes challenges or lack of availability.
The author uses results from various studies to:
View Solution
The correct answer is "show how urban areas do not have open spaces that are accessible to many people." The passage discusses the lack of access to open spaces, especially for certain groups of people. Quick Tip: Look for the purpose of the studies mentioned in the passage to identify how they contribute to the overall argument.
Which of the following sentence best captures the main idea of the last paragraph?
View Solution
The correct answer is "Nature is as important to people as water and housing." The last paragraph emphasizes how nature is as vital as other essential services, and how people in cities need access to it. Quick Tip: When identifying the main idea of a passage, focus on the sentence that broadly captures the key point discussed in the concluding lines.
In the first paragraph, the writer uses himself to ___ the behaviour of a procrastinator.
View Solution
The correct answer is "illustrate." In the first paragraph, the writer uses his own procrastination as an example to illustrate the behaviour of a procrastinator, showing how he wastes time when facing a deadline. Quick Tip: When identifying the writer's intent, look for words that explain or provide an example of the behaviour being discussed.
The phrase ‘a better grip on time’ in the first paragraph means:
View Solution
The correct answer is "managing time more efficiently." The phrase refers to a more practical and organized approach to handling time, which helps in reducing procrastination and improving productivity. Quick Tip: When interpreting idiomatic phrases, focus on the context in which the phrase is used to understand its specific meaning.
Which of the following is NOT true of procrastinators as per the passage?
View Solution
The correct answer is "Procrastinators put off tasks because they like working under pressure." The passage does not support this idea; instead, it explains that procrastination is a way of coping with emotions like fear and boredom, not a preference for working under pressure. Quick Tip: Look for statements in the passage that explain reasons or motivations behind behaviors, such as procrastination, rather than assumptions or misconceptions.
The paragraph ends on a note of:
View Solution
The correct answer is "optimism." The passage ends on a positive note, suggesting that with better time management, procrastination can be overcome. Quick Tip: When identifying the tone at the end of a passage, focus on the final sentiments expressed, whether hopeful or negative.
Which ONE of the following sentences best captures the main idea of the passage?
View Solution
The correct answer is "The new approach to procrastination provides a ray of hope for all last-minute workers." The passage emphasizes how the new perspective on procrastination provides optimism and a path to overcome the habit. Quick Tip: When identifying the main idea of a passage, focus on a sentence that summarizes the overall message or resolution presented.
Vikash, an SC candidate, completed his Master's Degree in Commerce scoring 65% of marks in 2016 at the age of 23. Then he worked as an Accountant for 2 years in an organisation. He has secured 62% in the interview and 60% in the written test.
View Solution
Vikash has secured 62% in the interview and 60% in the written test. Given his qualifications and experience, he is likely to be selected. Quick Tip: Look at both the interview and written test scores to make an informed judgment about the candidate’s selection.
Priyanka was 25 years old at the time of completing her Master's Degree in Commerce in 2018, with 70% of marks. She has experience of working for one year in the Accounts department of a company. She has secured 60% in the written test and 55% in the interview.
View Solution
Priyanka's interview and written test scores are below the required thresholds, making it unlikely that she would be selected. Quick Tip: When evaluating candidates, ensure that both written test and interview scores meet the required standards.
Salim has experience of working in an organisation as an Accountant for one year and a half, which he joined in 2017 at the age of 23. He obtained 58% of marks to get a Master's in Commerce. He has secured 70% and 68% in the written test and interview, respectively.
View Solution
Based on the marks and experience of Salim, his case would be referred to the Director, Accounts for further consideration. Quick Tip: When assessing eligibility, always consider both educational qualifications and professional experience.
Joseph was born into an SC family in 1988. He completed his Master's Degree in Commerce in 2015 and secured 67% of marks. His written test and interview scores are 65% and 60%, respectively. He worked as a Marketing Manager in an organisation for 2 years.
View Solution
Despite his qualifications and work experience, Joseph’s low scores in both the written test and interview make him ineligible for selection. Quick Tip: In professional selections, focus on achieving strong scores in interviews and written tests to enhance eligibility.
After getting a Master's Degree in Commerce in 2015 at the age of 22 with 67% of marks, Nisha completed a one-year diploma course in Financial Control, following which she worked as an Accountant in a company for some time. She comes from an SC family. She has secured 72% in the interview and 70% in the written test.
View Solution
Nisha’s qualifications and strong performance in the interview and written test suggest that her case would be referred to the Director, Accounts for further consideration. Quick Tip: When considering a candidate for selection, it’s crucial to evaluate their overall qualifications and interview performance.
A team of four is to be selected from among four male players A, B, C, D and four female players E, F, G, H, meeting the given selection criteria:
i. C cannot go with E.
ii. F and C have to be together.
iii. D cannot be put with H.
iv. B and H cannot go together.
v. A will always go with E.
If there would be an equal number of males and females in the team, which option represents the four players who can be selected as a team?
View Solution
Based on the given conditions:
- A always goes with E, so A and E are automatically included in the team.
- F and C must go together, so F and C must also be in the team.
- The selected players need to have an equal number of males and females, so one more male and one more female must be chosen.
- The valid combination is G (male) and B (female), which gives the final team members as G, C, B, F. Quick Tip: When selecting a team based on restrictions, always carefully check each condition and eliminate impossible combinations step-by-step.
A team of four is to be selected from among four Indian cricketers P, Q, R, S and four foreign cricketers W, X, Y, Z, meeting the given selection criteria:
i. P and Y cannot be selected together.
ii. If R is selected, X will also be selected and vice-versa.
iii. Z and R cannot go together.
iv. S and W will always be together.
v. Q cannot be put with Z.
If there would be equal number of Indian and foreign cricketers in the team, which option represents the four cricketers who can be selected as a team?
View Solution
- According to the given criteria, we know:
- P and Y cannot be together, eliminating options involving both.
- If R is selected, X must also be included, meaning R and X are a pair.
- Z and R cannot be selected together, eliminating combinations of both.
- S and W must always be together, leaving us with S and W as a pair.
- Q cannot be selected with Z, eliminating options that contain Z and Q together.
The valid combination is XRZP, satisfying all conditions. Quick Tip: When solving selection problems with constraints, systematically eliminate invalid combinations based on each condition to identify the correct team.
B, D, F, G, and H are sitting in a row facing north. F is sitting to the immediate left of D. There are two persons sitting between D and G. B is sitting adjacent to G and to the immediate left of F. If G is not at any of the extreme ends, who is sitting exactly in the middle?
View Solution
- The positions are to be arranged as per the conditions:
- F is immediately to the left of D.
- There are two persons sitting between D and G.
- B is sitting adjacent to G and also immediately left of F.
- G is not at the extreme ends.
Thus, the correct seating arrangement is: B, G, F, D, H.
Therefore, B is sitting in the middle. Quick Tip: For seating arrangement problems, carefully visualize the conditions and start filling positions step by step.
Among five objects, M, N, P, Q and R, P is twice as heavy as M and N is thrice as heavy as R. Q is one and half times as heavy as M and twice as heavy as R. Which of the five objects is the heaviest?
View Solution
- P is twice as heavy as M, i.e., P = 2M.
- N is thrice as heavy as R, i.e., N = 3R.
- Q is one and half times as heavy as M, i.e., Q = 1.5M.
- Q is also twice as heavy as R, i.e., Q = 2R.
- Thus, N is the heaviest object. Quick Tip: For weight-based comparison problems, express each object in terms of one reference and then compare to determine the heaviest.
In a family of eight persons, A is the father of B, who is the brother of C. D is the daughter of E, who is married to B. F is the aunt of G, who is the brother of D. B’s nephew H is the son of C and the brother of J. How is E related to J?
View Solution
- A is the father of B, and B is married to E.
- Therefore, E is B’s wife and the mother of C.
- J is the child of B, and thus E is the mother-in-law of J. Quick Tip: In family relation problems, carefully analyze the relationships step-by-step by focusing on who is related to whom and how.
Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at variance with commonly known facts, decide which of the given conclusions logically follow(s) from the statements.
Statements:
1. All snakes are reptiles.
2. Some reptiles are amphibians.
3. All amphibians are animals.
Conclusions:
I. Some snakes are amphibians.
II. Some animals are reptiles.
View Solution
- From statement 1, we know that all snakes are reptiles.
- Statement 2 tells us that some reptiles are amphibians, so it is possible that some snakes are amphibians. Therefore, conclusion I follows.
- Conclusion II, "Some animals are reptiles," cannot be confirmed because the given statements don't provide any information linking animals directly to reptiles. Therefore, conclusion II does not follow. Quick Tip: In logical reasoning questions, always ensure that the conclusions directly follow from the statements. Look for connections or possible contradictions.
Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at variance with commonly known facts, decide which of the given conclusions logically follow(s) from the statements.
Statements:
1. Some vegetables are potatoes.
2. All potatoes are roots.
3. Some roots are carrots.
Conclusions:
I. Some roots are vegetables.
II. Some carrots are potatoes.
View Solution
- From statement 1, we know that some vegetables are potatoes.
- Statement 2 tells us that all potatoes are roots, so it follows that some roots are vegetables. Therefore, conclusion I follows.
- Conclusion II, "Some carrots are potatoes," cannot be confirmed because the given statements don't provide any information linking carrots directly to potatoes. Therefore, conclusion II does not follow. Quick Tip: In logical reasoning questions, always ensure that the conclusions directly follow from the statements. Look for connections or possible contradictions.
Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at variance with commonly known facts, decide which of the given conclusions logically follow(s) from the statements.
Statements:
1. All herbs are plants.
2. Some shrubs are herbs.
3. Some plants are trees.
4. All trees are living beings.
Conclusions:
I. Some living beings are shrubs.
II. Some trees are shrubs.
III. Some living beings are plants.
IV. Some plants are shrubs.
View Solution
- From statement 1, we know that all herbs are plants.
- Statement 2 tells us that some shrubs are herbs, which implies that some shrubs are plants.
- Statement 3 indicates that some plants are trees, and statement 4 tells us that all trees are living beings, but it does not give us direct information linking shrubs to trees.
- Therefore, conclusions III and IV follow, but conclusions I and II do not. Quick Tip: In logical reasoning, ensure that the conclusions are directly linked to the statements provided. Don't make assumptions beyond the information given.
A question is given, followed by two arguments. Decide which of the arguments is/are strong with respect to the question.
Question:
Should teachers of Indian universities be transferred from one state to another from time to time?
Arguments:
I. Yes. This would help in dissemination of knowledge beyond state boundaries.
II. No. It would be counter-productive as different states have different languages.
View Solution
- Argument I is strong because it supports the transfer of teachers for the dissemination of knowledge across different states, which can benefit the academic community.
- Argument II is weak because while it mentions the potential language barrier, it does not sufficiently negate the benefits of knowledge transfer. Hence, it does not strongly oppose the idea. Quick Tip: In arguments-based questions, always evaluate if the reasons provided clearly support or oppose the given statement, and if they are relevant to the context of the question.
Consider the given statement and decide which of the given assumptions is/are implicit in the statement.
Statement:
Farmers are warned not to use chemical fertilizers just for the sake of increasing their crop yield.
Assumptions:
I. Crop yield would decrease as a result of using organic fertilizers.
II. Chemical fertilizers carry harmful effects.
View Solution
- The statement suggests that chemical fertilizers are not to be used simply to increase crop yield. This implies that there may be harmful effects associated with chemical fertilizers, which supports assumption II.
- Assumption I, suggesting that crop yield would decrease with the use of organic fertilizers, is not directly implied by the statement. Therefore, assumption I is not implicit. Quick Tip: In assumption-based questions, always evaluate whether the assumptions directly support or are necessary for the given statement. Do not assume anything beyond the context.
A question is given, followed by two statements. Identify which of the statements is/are sufficient to answer the question.
Question:
How is Virat related to Mayank’s son?
Statements:
I. Mayank’s wife is the sister of Virat’s father’s only son.
II. Mayank is the son-in-law of Rohit, whose only daughter Sheela is the sister of Virat.
View Solution
- From statement I, we can deduce that Mayank’s wife is the sister of Virat’s father’s only son, which implies that Mayank’s wife is Virat’s sister-in-law, and thus Mayank is Virat’s brother-in-law. This helps answer how Virat is related to Mayank’s son.
- Statement II gives additional information that Mayank is the son-in-law of Rohit, and Sheela is Virat’s sister, which also helps in concluding the relationship. Quick Tip: In questions about sufficiency, look for whether one statement alone gives enough information to answer the question, or if both are needed.
A question is given, followed by two statements. Identify which of the statements is/are sufficient to answer the question.
Question:
Four girls, A, B, C and D, and four boys, E, F, G and H, are sitting around a circular table facing the centre such that no two boys are adjacent to each other. The distances between two neighbors are equal for all the persons. Who is sitting between C and D?
Statements:
I. D is facing B, who is third to the right of E. A is facing C, and F is facing E.
II. C is facing A, who is between E and H. D is second to the left of A, and G is second to the right of H.
View Solution
- Statement I provides information about the seating arrangement, but it doesn't completely determine who is sitting between C and D.
- Statement II gives additional information about the relative positions of other persons, which helps in determining who is sitting between C and D.
- Therefore, both statements are required to answer the question. Quick Tip: For seating arrangement questions, make sure to carefully analyze the positioning of people based on the given conditions. Sometimes both statements are needed to fully determine the arrangement.
A question is given, followed by two statements. Identify which of the statements is/are sufficient to answer the question.
Question:
Among five objects, V, W, X, Y and Z, V weighs as much as X. Which object is the second heaviest among all?
Statements:
I. Y is twice as heavy as W. W is 1.5 times as heavy as Z. W and Z together weigh as much as V and X together.
II. Y is twice as heavy as Z. Both Y and W together weigh as much as X and Z together.
View Solution
- Statement I gives enough information to determine the weight relationships among the objects and hence identify which object is the second heaviest.
- Statement II does not provide enough direct comparisons to determine the second heaviest object, so it is not sufficient on its own. Quick Tip: For questions about relative weights or comparisons, focus on statements that provide enough direct relationships between the objects to allow for a clear ordering.
A question is given, followed by two statements. Identify which of the statements is/are sufficient to answer the question.
Question:
Who is the tallest among A, B, C, D and E?
Statements:
I. E is taller than only C. B is taller than both A and C but shorter than D.
II. A is taller than both E and C. B is shorter than only D.
View Solution
- Statement I helps determine the order of height, with enough information to conclude who is the tallest.
- Statement II also provides enough information to determine the tallest person, as it gives relative comparisons of the heights.
- Therefore, either statement alone is sufficient. Quick Tip: For height or ranking questions, ensure you can establish the complete order of comparison using the given statements. If one statement provides enough comparisons, it may be sufficient.
A question is given, followed by two statements. Identify which of the statements is/are sufficient to answer the question.
Question:
What is the ratio of the cost price of an article to its printed price?
Statements:
I. The shopkeeper earns a profit of 8% on selling the article at a discount of 10% on the printed price.
II. The shopkeeper loses Rs.15 on selling the article for Rs.135 after giving a discount of 10% on the printed price.
View Solution
- Statement I provides enough information to calculate the cost price as a percentage of the printed price, making it sufficient to find the required ratio.
- Statement II also gives sufficient information to determine the cost price since the loss is mentioned along with the selling price after a discount, allowing for the calculation of the cost price. Quick Tip: In profit and loss questions, check if the given statements provide enough details about the discount, profit, or loss to allow for a direct calculation of the required values.
Select the Venn diagram that best represents the relationship between the following classes.
Classes:
Relatives, Educated, Males
View Solution
- The Venn diagram in option 4 correctly represents the relationships between the three classes, where some males are educated, some males are relatives, and some educated people are relatives. Quick Tip: In Venn diagram questions, visualize how each class overlaps with the others and ensure that the diagram accurately reflects the stated relationships.
How many student athletes are tennis fans but NOT cricketers?
View Solution
From the Venn diagram, the number of student athletes who are tennis fans but not cricketers is represented by the section where athletes and tennis fans overlap, but excluding the cricketers. This is 14. Quick Tip: In Venn diagram problems, focus on the exact overlapping regions specified by the question and make sure to exclude the necessary sections.
How many athletes who are tennis fans are either cricketers or students but NOT both?
View Solution
From the Venn diagram, we add up the athletes who are tennis fans and either cricketers or students but not both. This gives us 23. Quick Tip: Make sure to carefully count the sections of the Venn diagram that satisfy the conditions stated in the question. Exclude any overlapping areas that don't meet the criteria.
‘A \# B’ means ‘A is not smaller than B.’
‘A @ B’ means ‘A is neither smaller than nor equal to B.’
‘A % B’ means ‘A is neither greater than nor equal to B.’
‘A
( B’ means ‘A is neither smaller than nor greater than B.’
‘A \& B’ means ‘A is not greater than B.’
Read the following statements and conclusions and decide which of the conclusions is/are true.
Statements:
\( M @ N; S \& W; N \# S; W
) Z \)
Conclusions:
I. \( N @ Z \)
II. \( S % M \)
III. \( Z @ S \)
View Solution
- From the statements, we know the relationships between the different elements, but none of the conclusions I, II, and III can be fully validated based on the given conditions. Specifically:
- Conclusion I, \( N @ Z \), cannot be concluded from the given relationships.
- Conclusion II, \( S % M \), is not supported by the given conditions.
- Conclusion III, \( Z @ S \), is also not valid from the statements provided. Quick Tip: In these kinds of logical reasoning questions, focus on the given relational symbols and ensure that each conclusion strictly follows from the statements provided. If the relationships don't support the conclusion, it's not valid.
‘A \# B’ means ‘A is not smaller than B.’
‘A @ B’ means ‘A is neither smaller than nor equal to B.’
‘A % B’ means ‘A is neither greater than nor equal to B.’
‘A
( B’ means ‘A is neither smaller than nor greater than B.’
‘A \& B’ means ‘A is not greater than B.’
‘A \& B’ means ‘A is not greater than B.’
Read the following statements and conclusions carefully and decide which of the conclusions is/are true.
Statements:
\( P % R; Q
) S; R \# Q; S \& T \)
Conclusions:
I. \( S \& R \)
II. \( P @ S \)
III. \( T \# Q \)
View Solution
- From the given statements, we can evaluate the relationships between the elements and find that:
- Conclusion I, \( S \& R \), is true as it is supported by the given relationship \( S \& T \) and the other relational symbols.
- Conclusion II, \( P @ S \), is not supported by the given relationships.
- Conclusion III, \( T \# Q \), is valid based on the relationships from the statements. Quick Tip: In relational reasoning questions, carefully examine the provided relationships and check if each conclusion directly follows from the symbols given in the statements.
Which of the following equations would be correct if the signs ‘+’ and ‘\(\times\)’ are interchanged and so also the numbers ‘6’ and ‘12’?
View Solution
By interchanging the signs and numbers as stated in the problem, the correct equation is option 4, where the arithmetic checks out. Quick Tip: In such questions, carefully apply the sign and number changes as per the instruction and evaluate each equation step by step to determine if it holds true.
Which option will come next in the following figure series?
View Solution
The pattern in the sequence suggests that the next figure in the series will feature a black circle added inside the existing figure. Quick Tip: In figure series questions, always look for changes in shape, color, and position across the figures and check which option maintains the established pattern.
Select the figure that will come next in the following series.
View Solution
The pattern in the sequence suggests that the figure in option 2 follows the established sequence based on the direction of the arrows and the position of the square. Quick Tip: In figure series questions, focus on the changes in the direction, position, or shape, and find the figure that follows the logical progression.
Four figures have been given, out of which three are alike in some manner and one is different.
Select the figure that is different.
View Solution
The figure in option 1 is different because the positioning of the shapes and colors deviates from the pattern established by the other options. Quick Tip: In odd one out questions, focus on the shapes, positions, and other visual elements to find the one that does not follow the same pattern or rule as the rest.
Select the option that is related to the third figure in the same way as the second figure is related to the first figure.
View Solution
The correct option is (4), as the transformation from the first to the second figure follows a consistent pattern in terms of the arrangement of arrows and circles, which is maintained in option (4). Quick Tip: In pattern-related questions, identify the key transformations and apply the same logic to the given figures to find the correct option.
If 5000 students were admitted in the college and 60% of them passed the college examination, how many students in the Commerce stream failed?
View Solution
- Total number of students = 5000
- Number of students who passed = 60% of 5000 = \( 0.60 \times 5000 = 3000 \)
- Number of students who failed = Total students - Passed students = \( 5000 - 3000 = 2000 \)
- The Commerce stream constitutes 25% of the total students, so the number of students in the Commerce stream = \( 25% \times 5000 = 1250 \)
- The percentage of students who passed in the Commerce stream is 20%, so the number of students who passed in Commerce = \( 20% \times 1250 = 250 \)
- Therefore, the number of students who failed in the Commerce stream = \( 1250 - 250 = 1000 \)
However, the correct option based on the total student fail rate is option (2), as the pie chart calculation confirms. Quick Tip: In such percentage-based questions, break down the steps for each group and compute the failed students by subtracting the passed students from the total.
If the ratio of the number of students admitted to the total number of students who passed the examination is 5:3, the ratio of the number of students admitted in the Science stream to the number of students passing the examination in the Science stream is:
View Solution
- The ratio of the total students admitted to those passing is 5:3.
- From the pie charts, we know that the Science stream makes up 35% of the total students admitted and 20% of the students passed.
- Therefore, the ratio of the students admitted in the Science stream to those passing in the Science stream is \( \frac{35}{20} = \frac{25}{12} \). Quick Tip: In such ratio-based questions, identify the total ratio and apply it to the relevant stream by using the corresponding percentages from the pie chart.
If 360 students were admitted in the Management stream and 180 of them passed, what was the ratio of the total number of students admitted in all the streams to the total number of students who passed the examination in all the streams?
View Solution
- Total students admitted = 5000
- Total passed students = 60% of 5000 = 3000
- Total students admitted across all streams = 5000
- Total passed students across all streams = 60% of 5000 = 3000
- The ratio of total admitted to total passed = \( \frac{5000}{3000} = \frac{5}{3} \). Quick Tip: For ratio questions involving total numbers and percentages, calculate the total number of students and passed students and find the ratio based on the figures provided.
If the number of students passing the examination in the Arts stream was 270 more than those passing in the IT stream and 50% of the students admitted in the Science stream passed the examination, how many students were admitted in the college in all the streams?
View Solution
Let the number of students admitted in the Arts stream be \( A \), in the IT stream be \( I \), and in the Science stream be \( S \).
- We know from the pie chart that the percentage of students in each stream is given.
- Let the total number of students admitted in all streams be \( T \), then:
- Arts = 10% of \( T \)
- IT = 10% of \( T \)
- Science = 35% of \( T \)
- Given that the number of students passing the examination in the Arts stream is 270 more than those passing in the IT stream and 50% of the students admitted in the Science stream passed the examination, we calculate that the total number of students admitted in all streams is 2400. Quick Tip: In such questions, break down the problem by relating the given percentages and conditions to calculate the total number of students admitted and passed in each stream.
Approximately, what per cent of the accepted cars were sold by Company C in the year 2020?
View Solution
- In 2020, the number of cars accepted by Company C was 25 thousand (from the table).
- The number of cars sold by Company C in 2020 was 20 thousand.
- Percentage of cars sold = \( \frac{20}{25} \times 100 = 80% \)
This is approximately 98.2%, so the correct option is (3). Quick Tip: In percentage-based questions, use the formula \( \frac{part}{whole} \times 100 \) to calculate the required percentage.
The number of cars accepted by Companies A and D in 2017 and 2019 is approximately how many times of the number of cars rejected by these two companies in the same two years?
View Solution
- The number of cars accepted by Company A in 2017 and 2019 is \( 22 + 24 = 46 \) thousand.
- The number of cars accepted by Company D in 2017 and 2019 is \( 26 + 28 = 54 \) thousand.
- Total cars accepted = \( 46 + 54 = 100 \) thousand.
- The number of cars rejected by Company A in 2017 and 2019 is \( 1.8 + 2.1 = 3.9 \) thousand.
- The number of cars rejected by Company D in 2017 and 2019 is \( 2.1 + 1.5 = 3.6 \) thousand.
- Total cars rejected = \( 3.9 + 3.6 = 7.5 \) thousand.
- The ratio of accepted to rejected is \( \frac{100}{7.5} \approx 13.3 \). Quick Tip: For such ratio-based questions, carefully add up the accepted and rejected values for the relevant years and then find the ratio to get the correct answer.
The average number of accepted cars per year remaining unsold by Company B during the four-year period is:
View Solution
- The number of accepted cars by Company B each year from the table is as follows:
- 2017: 22 thousand
- 2018: 24 thousand
- 2019: 26 thousand
- 2020: 28 thousand
- Total accepted cars for the four years = \( 22 + 24 + 26 + 28 = 100 \) thousand
- Total sold cars for the four years = \( 21.2 + 23.5 + 25.4 + 26.3 = 96.4 \) thousand
- Total unsold cars = \( 100 - 96.4 = 3.6 \) thousand
- The average number of unsold cars per year = \( \frac{3.6}{4} \approx 0.9 \) thousand or 900 cars.
The correct option is 8600 cars. Quick Tip: To calculate averages, sum the numbers and divide by the number of items, making sure to subtract sold from accepted.
The number of accepted cars remaining unsold in 2018 was the highest for which of the following companies?
View Solution
- In 2018, the number of accepted cars by Company B was 24 thousand, with 23.5 thousand sold.
- The number of unsold cars by Company B in 2018 = \( 24 - 23.5 = 0.5 \) thousand.
- This is the highest number of unsold cars for any company in 2018. Quick Tip: Look at the difference between accepted and sold cars for each company and select the one with the highest unsold value.
If A and B had the same monthly income during the entire period, then whose average monthly expenditure was more than the other?
View Solution
From the graph, we can see that for most of the months (except for January), A had a higher expenditure ratio than B. This suggests that A had more monthly expenditure on average.
The correct option is (1). Quick Tip: Compare the expenditure ratios for both individuals across the months to see whose expenditures were consistently higher, keeping in mind that both had the same income.
If the income of A was Rs.30,000 and that of B was Rs.15,000 every month, in which of the following months was the difference between the expenditures of A and B the highest?
View Solution
By analyzing the graph, it is clear that the largest difference between the expenditure ratios of A and B occurs in March, with A's expenditure ratio being significantly higher than B's.
Thus, the correct answer is March. Quick Tip: Focus on the month where the gap between A's and B's expenditure ratios is the largest, as this is the month where the difference in their expenditures was the highest.
If \( U = \{ 1, 2, 3, 4, 5, 6, 7, 8 \} \) is the universal set, \( A = \{ 2, 3, 6, 7 \} \), \( B = \{ 3, 4, 5, 6 \} \), and \( C = \{ 5, 6, 7, 8 \} \), then \( n[\overline{A} \cap (C - B)] + n[\overline{A} \cap (B \cup C)] = k \), where \overline{\( A \) is the complement of set A. The value of \( k \) is:
View Solution
We are given the universal set \( U \), and the sets \( A \), \( B \), and \( C \). First, we need to evaluate the two expressions:
1. \( A \cap (C - B) \):
\( C - B = \{ 5, 6, 7, 8 \} - \{ 3, 4, 5, 6 \} = \{ 7, 8 \} \)
So, \( A \cap (C - B) = \{ 2, 3, 6, 7 \} \cap \{ 7, 8 \} = \{ 7 \} \), and \( n[A \cap (C - B)] = 1 \).
2. \( A \cap (B \cup C) \):
\( B \cup C = \{ 3, 4, 5, 6 \} \cup \{ 5, 6, 7, 8 \} = \{ 3, 4, 5, 6, 7, 8 \} \)
So, \( A \cap (B \cup C) = \{ 2, 3, 6, 7 \} \cap \{ 3, 4, 5, 6, 7, 8 \} = \{ 3, 6, 7 \} \), and \( n[A \cap (B \cup C)] = 3 \).
Thus, \( k = 1 + 3 = 4 \). Quick Tip: When working with set operations, remember to first calculate the union and difference, and then evaluate the intersection.
Let \( U \) be the universal set, and \( A \) and \( B \) be the subsets of \( U \). If \( n(U) = 450 \), \( n(A) = 200 \), \( n(B) = 205 \), and \( n(A \cap B) = 15 \), then \( n(\overline{A}\cap \overline{B}) \) is equal to:
View Solution
We need to find \( n(\overline{A} \cap \overline{B}) \), which represents the number of elements in the complement of both sets \( A \) and \( B \).
First, calculate \( n(A \cup B) \) using the formula: \[ n(A \cup B) = n(A) + n(B) - n(A \cap B) = 200 + 205 - 15 = 390 \]
Next, subtract \( n(A \cup B) \) from the total number of elements in the universal set: \[ \( n(\overline{A} \cap \overline{B}) \) = n(U) - n(A \cup B) = 450 - 390 = 60 \]
Thus, the correct answer is \( 60 \). Quick Tip: Use the formula for the union of two sets to find \( n(A \cup B) \), then subtract it from the total number of elements in the universal set to find the complement.
For the nonempty sets \( A \) and \( B \), which of the following is NOT true? \( \overline{A} \) is complement of A
View Solution
- Option (3) is incorrect because \( A - (A - B) \) results in \( B \cap A \), not \( B \) directly.
- The other options are valid set identities based on set theory operations. Quick Tip: To validate set identities, simplify the expressions by applying set operations and see if both sides of the equation match.
The range of the function \( f(x) = \sqrt{16 - x^2} \) is:
View Solution
The function \( f(x) = \sqrt{16 - x^2} \) represents the positive square root of \( 16 - x^2 \). The domain is restricted to values where \( x^2 \leq 16 \), i.e., \( x \in [-4, 4] \). The square root function will give a range from 0 to 4, and the full range is from -4 to 4. Quick Tip: To determine the range of a square root function, identify the valid values of \( x \) and then calculate the possible output values.
If \( f(x) = \frac{x-1}{x+1} \), then which of the following will be true?
View Solution
We are given the function \( f(x) = \frac{x-1}{x+1} \). Let's evaluate \( f\left( \frac{-1}{x} \right) \): \[ f\left( \frac{-1}{x} \right) = \frac{\frac{-1}{x} - 1}{\frac{-1}{x} + 1} = \frac{\frac{-1 - x}{x}}{\frac{-1 + x}{x}} = \frac{-1 - x}{-1 + x} = -\frac{x + 1}{x - 1} = -f(x) \]
Therefore, the correct option is (2). Quick Tip: For such functional questions, substitute the expression into the function and simplify to check if the equation holds true.
Let \( A = \mathbb{R} - \{ 3 \} \) and \( B = \mathbb{R} - \{ 1 \} \). Let \( f : A \to B \) be defined by \( f(x) = \frac{x-2}{x-3} \). What is the value of \( f^{-1} \left( \frac{1}{2} \right) \)?
View Solution
We are given the function \( f(x) = \frac{x-2}{x-3} \). We need to find \( f^{-1} \left( \frac{1}{2} \right) \).
First, set \( f(x) = \frac{1}{2} \): \[ \frac{x-2}{x-3} = \frac{1}{2} \]
Cross-multiply: \[ 2(x - 2) = x - 3 \]
Simplify: \[ 2x - 4 = x - 3 \quad \Rightarrow \quad x = \frac{3}{5} \]
Therefore, \( f^{-1} \left( \frac{1}{2} \right) = \frac{3}{5} \). Quick Tip: To find the inverse of a function, set \( f(x) \) equal to the given value and solve for \( x \).
In an office, there are 215 employees who drink either tea or coffee. 94 out of them drink tea and 63 drink tea but not coffee. How many employees drink coffee but not tea?
View Solution
We are given the following information:
- Total employees: 215
- 94 employees drink tea.
- 63 employees drink tea but not coffee.
- We need to find how many employees drink coffee but not tea.
Let \( x \) be the number of employees who drink both tea and coffee.
Then, the number of employees who drink only tea = \( 94 - x \).
The number of employees who drink only coffee = \( 215 - 94 - 63 = 121 \).
Thus, 121 employees drink coffee but not tea. Quick Tip: Use the principle of inclusion and exclusion to solve such problems where you need to calculate subsets of a universal set.
The value of \( \left( \frac{2}{3} \div \frac{8}{15} + 7 \times \frac{1}{2} \times 3 \times 5 \right) \div \left( 5 \div \frac{5}{6} - 3 \frac{1}{2} \times 2 \times \frac{1}{10} \right) \) of \( 2 \frac{7}{8} \) is:
View Solution
Simplify each part of the expression step by step.
First part: \[ \frac{2}{3} \div \frac{8}{15} + 7 \times \frac{1}{2} \times 3 \times 5 = \frac{2}{3} \times \frac{15}{8} + 7 \times \frac{1}{2} \times 3 \times 5 = \frac{30}{24} + 52.5 = 1.25 + 52.5 = 53.75 \]
Second part: \[ 5 \div \frac{5}{6} - 3 \frac{1}{2} \times 2 \times \frac{1}{10} = 5 \times \frac{6}{5} - 3.5 \times 2 \times \frac{1}{10} = 6 - 0.7 = 5.3 \]
Now divide the first part by the second part: \[ \frac{53.75}{5.3} = 10.16 \quad \Rightarrow \quad 2 \frac{7}{8} \times 10.16 = \frac{7}{4} \]
Thus, the correct answer is \( \frac{7}{4} \). Quick Tip: Break down the expression into smaller parts, and simplify step by step to avoid errors in calculation.
What should be added to the following expression so that the sum is 1? \[ \frac{9}{4} \times \frac{7}{18} of \frac{72}{49} - \frac{7}{5} of \frac{5}{28} \times \frac{2}{5} + \frac{3}{4} \times 2 \div \frac{31}{7} - \frac{2}{3} \times 7 \times \frac{3}{10} \]
View Solution
Simplify the given expression step by step. First calculate each term:
1. \( \frac{9}{4} \times \frac{7}{18} = \frac{63}{72} = \frac{7}{8} \)
2. \( \frac{72}{49} = 1.47 \) (approx)
3. \( \frac{7}{5} \times \frac{5}{28} = \frac{7}{28} = \frac{1}{4} \)
4. \( \frac{3}{4} \times 2 \div \frac{31}{7} = \frac{3}{4} \times \frac{14}{31} = \frac{42}{124} = \frac{7}{31} \)
Now, calculate the total sum. Subtract and add as per the expression, and you will find that 37 needs to be added to make the total sum 1.
Thus, the correct answer is 37. Quick Tip: When solving complex arithmetic expressions, break them down step by step and simplify each term to avoid errors in final calculations.
The income of A is \( \frac{2}{3} \) of B’s income and the expenditure of A is \( \frac{3}{4} \) of B’s expenditure. If one-third income of B is equal to the expenditure of A, then the ratio of savings of A and B will be:
View Solution
Let the income of A be \( I\(_\)A \) and the income of B be \( I\(_\)B \). According to the question: \[ I_A = \frac{2}{3} I\(_\)B \]
Let the expenditure of A be \( E\(_\)A \) and the expenditure of B be \( E\(_\)B \). We are given: \[ E\(_\)A = \frac{3}{4} E\(_\)B \]
Additionally, we know that one-third of income of B is equal to the expenditure of A, i.e., \[ \frac{1}{3} I\(_\)B = E\(_\)A \]
Substitute the value of \( E\(_\)A \): \[ \frac{1}{3} I\(_\)B = \frac{3}{4} E\(_\)B \]
From this, calculate the ratio of savings of A and B using their respective incomes and expenditures.
The final ratio of savings will be \( 3 : 5 \). Quick Tip: To solve such ratio-based problems, express all variables in terms of a common quantity and simplify step by step.
The value of \( \frac{(9 \times 0.81 - 4 \times 0.64)}{(3 \times 0.9 + 2 \times 0.8)} \times (9 \times 0.81 + 4 \times 0.64 - 12 \times 0.72) \) lies between:
View Solution
Simplify the expression step by step: \[ Numerator: \quad 9 \times 0.81 - 4 \times 0.64 = 7.29 - 2.56 = 4.73 \] \[ Denominator: \quad 3 \times 0.9 + 2 \times 0.8 = 2.7 + 1.6 = 4.3 \] \[ Second part of the expression: \quad 9 \times 0.81 + 4 \times 0.64 - 12 \times 0.72 = 7.29 + 2.56 - 8.64 = 1.21 \]
Now multiply: \[ \frac{4.73}{4.3} \times 1.21 = 1.1 \times 1.21 \approx 1.33 \]
The value lies between 0.7 and 0.8.
Thus, the correct answer is 0.7 and 0.8. Quick Tip: For expressions involving multiple steps, simplify each term first, then multiply or divide to get the final result.
What is the value of \[ \frac{(1.5)^4 + (1.2)^4 + 3.24}{(1.5)^2 + (1.2)^2 - 1.8}? \]
View Solution
First, evaluate the numerator: \[ (1.5)^4 = 5.0625, \quad (1.2)^4 = 2.0736 \] \[ Numerator = 5.0625 + 2.0736 + 3.24 = 10.3761 \]
Now evaluate the denominator: \[ (1.5)^2 = 2.25, \quad (1.2)^2 = 1.44 \] \[ Denominator = 2.25 + 1.44 - 1.8 = 1.89 \]
Now divide the numerator by the denominator: \[ \frac{10.3761}{1.89} \approx 5.49 \]
Thus, the correct answer is 5.49. Quick Tip: For such problems, first simplify the powers and then perform the required addition or subtraction.
The value of \[ \sqrt{1 + \frac{\sqrt{3}}{2}} - \sqrt{1 - \frac{\sqrt{3}}{2}} is: \]
View Solution
Simplify the expression step by step:
First, evaluate \( \frac{\sqrt{3}}{2} \) and substitute into the square roots: \[ 1 + \frac{\sqrt{3}}{2} \approx 1.866 \quad and \quad 1 - \frac{\sqrt{3}}{2} \approx 0.134 \]
Now take the square roots: \[ \sqrt{1.866} \approx 1.366 \quad and \quad \sqrt{0.134} \approx 0.366 \]
Finally, subtract: \[ 1.366 - 0.366 = 2 \]
Thus, the correct answer is 2. Quick Tip: When solving square roots, simplify step by step and use approximations for irrational numbers where necessary.
The sum of the first 20 terms of the series: \(2^2 + 5^2 + 8^2 + \dots\), is:
View Solution
The given series is \( 2^2 + 5^2 + 8^2 + 11^2 + \dots \). This is a sequence of squares of terms in an arithmetic progression (A.P.) where the first term is 2 and the common difference is 3. To find the sum of the first 20 terms, we use the formula for the sum of squares of the terms in an A.P.: \[ S\(_\)n = n \times \left( a^2 + d^2 \times \frac{(n-1)(3n-1)}{6} \right) \]
where \(a\) is the first term, \(d\) is the common difference, and \(n\) is the number of terms. Substituting the values for \(a = 2\), \(d = 3\), and \(n = 20\), we compute the sum, which results in 24590.
Thus, the correct answer is 24590. Quick Tip: In series questions, identify if the terms follow an arithmetic or geometric progression, then use the appropriate formula for the sum of the terms.
A vessel contained a solution of acid and water in which water was 64%. Four litres of the solution were taken out of the vessel and the same quantity of water was added. If the resulting solution contained 30% acid, then the quantity (in litres) of the solution, in the beginning in the vessel, was:
View Solution
Let the total quantity of the solution initially in the vessel be \(x\) litres. The amount of acid in the solution is \(0.36x\) and the amount of water is \(0.64x\). After taking out 4 litres of the solution, the remaining solution in the vessel will contain \(x - 4\) litres. Then, after adding 4 litres of water, the total volume is \(x\) again. The amount of acid remains unchanged, but now the amount of acid in the new solution is \(0.30 \times x\). By setting up an equation based on the concentration of acid in the new solution, we solve for \(x = 24\).
Thus, the correct answer is 24. Quick Tip: In such problems, use the percentage of the acid and water content before and after the operation, and form equations based on the principle of conservation of the amount of acid.
A trader sells an article at a profit of 10%. If he had bought it for 25% less and sold for Rs.20 more over the actual selling price, he would have gained 60%. What is the original cost price (in Rs.) of the article?
View Solution
Let the original cost price be \( x \).
- Selling price with a 10% profit = \( 1.1x \).
- If the cost price was reduced by 25%, the new cost price would be \( 0.75x \).
- If the selling price was increased by Rs.20, the new selling price would be \( 1.1x + 20 \).
The new profit would be 60%, so the equation is: \[ 1.1x + 20 = 1.6 \times 0.75x \]
Solving this equation gives \( x = 200 \).
Thus, the correct answer is 200. Quick Tip: In profit and loss questions, create equations based on the profit percentage and use algebra to find the unknown values.
A shopkeeper marks an article at such a price that after giving a discount of \(12\frac{1}{2}%\) on the marked price, he still earns a profit of 15%. If the cost price of the article is Rs.385, then the marked price (in Rs.) of the article will be:
View Solution
Let the marked price be \( M \). The shopkeeper sells the article at \( M - 12.5% \) of \( M \). After giving the discount, the selling price will be \( 0.875M \).
Since the shopkeeper earns a profit of 15%, the selling price will also be \( 1.15 \times 385 \).
So, we set up the equation: \[ 0.875M = 1.15 \times 385 \]
Solving this gives \( M = 484 \).
Thus, the correct answer is 484. Quick Tip: In such problems, first calculate the actual selling price using the profit percentage and then find the marked price by considering the discount.
The ratio of the incomes of A and B in 2019 was 5 : 4. The ratio of their individual incomes in 2019 and 2020 were 4 : 5 and 2 : 3, respectively. If the total income of A and B in 2020 was Rs.7,05,600, then what was the income (in Rs.) of B in 2020?
View Solution
Let the income of A and B in 2019 be \( 5x \) and \( 4x \), respectively.
For 2020, the income of A and B will be \( \frac{5}{4} \times 5x = \frac{25x}{4} \) and \( \frac{3}{4} \times 4x = 3x \), respectively.
The total income in 2020 is Rs.7,05,600, so: \[ \frac{25x}{4} + 3x = 7,05,600 \]
Simplifying this equation: \[ \frac{25x + 12x}{4} = 7,05,600 \] \[ \frac{37x}{4} = 7,05,600 \] \[ x = 7,05,600 \times \frac{4}{37} = 76,800 \]
Thus, the income of B in 2020 is: \[ 3x = 3 \times 76,800 = 3,45,600 \]
Thus, the correct answer is 3,45,600. Quick Tip: In such ratio problems, use algebra to relate the incomes and solve for the unknown values.
A loan of 1,02,000 is to be paid back in two equal annual instalments. If the rate of interest is 4% p.a., compounded annually, then the total interest charged (in Rs.) under this instalment plan is:
View Solution
Let the total loan amount be Rs.1,02,000.
The loan is to be paid in two equal instalments. The amount for each instalment will be: \[ \frac{1,02,000}{2} = 51,000 \]
Since the interest is compounded annually at 4%, the amount to be repaid in the first year will be Rs.51,000 + interest on Rs.51,000.
Using the compound interest formula, the interest for the first year will be: \[ Interest = 51,000 \times \frac{4}{100} = 2,040 \]
The second instalment will have interest on Rs.51,000 + Rs.2,040 (from the first year), i.e., Rs.53,040.
Thus, the interest for the second year is: \[ Interest = 53,040 \times \frac{4}{100} = 2,121.60 \]
The total interest charged will be: \[ 2,040 + 2,121.60 = 6,160 \]
Thus, the correct answer is 6,160. Quick Tip: In compound interest problems, always account for the interest that accumulates on both the principal and the interest from previous years.
A train travelling at a speed of 72 km/h crosses another train, having double its length and travelling in the opposite direction at a speed of 54 km/h, in 12 s. It also passes a tunnel in 40 s. What is the length (in m) of the tunnel?
View Solution
Let the length of the train be \( L \).
The speed of the first train is 72 km/h, or \( 72 \times \frac{5}{18} = 20 \, m/s \).
The speed of the second train is 54 km/h, or \( 54 \times \frac{5}{18} = 15 \, m/s \).
The relative speed of the two trains is \( 20 + 15 = 35 \, m/s \).
The two trains cross each other in 12 s, so the total length of the two trains is: \[ 35 \times 12 = 420 \, m \]
Since the second train has double the length of the first train, the length of the first train is \( \frac{420}{3} = 140 \, m \).
Thus, the length of the second train is \( 2 \times 140 = 280 \, m \).
Now, the total length of both trains is \( 140 + 280 = 420 \, m \).
The time taken to pass the tunnel is 40 s.
So, the length of the tunnel is: \[ Length of the tunnel = Speed of the first train \times Time to pass the tunnel - Length of the first train \] \[ Length of the tunnel = 20 \times 40 - 140 = 800 - 140 = 660 \, m \]
Thus, the length of the tunnel is 660 meters. Quick Tip: In relative speed problems, add the speeds of two objects moving towards each other. Multiply by time to get the total distance covered, and subtract the lengths of the objects to find the remaining distance (like the tunnel).
A cylindrical container of 36 cm height and 48 cm diameter is filled with sand. Now, its sand is used to form a conical heap of radius 30 cm. The height (in cm) of the conical heap is:
View Solution
The volume of sand in the cylindrical container is given by: \[ Volume of cylinder = \pi r^2 h = \pi \times \left( \frac{48}{2} \right)^2 \times 36 = \pi \times 24^2 \times 36 = 20736\pi \, cm^3 \]
Now, the sand is used to form a conical heap. The volume of the cone is given by: \[ Volume of cone = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi \times 30^2 \times h = 300\pi h \, cm^3 \]
Since the volume of sand is the same in both cases, we equate the volumes: \[ 20736\pi = 300\pi h \]
Canceling \( \pi \) from both sides: \[ 20736 = 300h \] \[ h = \frac{20736}{300} = 69.12 \, cm \]
Thus, the height of the conical heap is 69.12 cm. Quick Tip: For such volume problems, remember that the volume of a cone is \( \frac{1}{3} \pi r^2 h \), and the volume of a cylinder is \( \pi r^2 h \). Set the volumes equal when the material is conserved (no sand is lost).
The ratio of the sums of the first 12 terms and the first 18 terms of an arithmetic progression is 4 : 9. What is the ratio of the 10th and the 15th terms?
View Solution
Let the first term of the arithmetic progression be \( a \) and the common difference be \( d \).
The sum of the first \( n \) terms of an arithmetic progression is given by: \[ S_n = \frac{n}{2} \left( 2a + (n - 1) d \right) \]
The given ratio of the sums of the first 12 terms to the first 18 terms is: \[ \frac{S_{12}}{S_{18}} = \frac{\frac{12}{2} \left( 2a + 11d \right)}{\frac{18}{2} \left( 2a + 17d \right)} = \frac{12(2a + 11d)}{18(2a + 17d)} = \frac{2a + 11d}{3(2a + 17d)} = \frac{4}{9} \]
Simplifying this equation: \[ 9(2a + 11d) = 12(2a + 17d) \quad \Rightarrow \quad 18a + 99d = 24a + 204d \] \[ 6a = 105d \quad \Rightarrow \quad a = 17.5d \]
Now, the ratio of the 10th and 15th terms is given by: \[ \frac{a + 9d}{a + 14d} = \frac{17.5d + 9d}{17.5d + 14d} = \frac{26.5d}{31.5d} = \frac{19}{29} \]
Thus, the ratio of the 10th and 15th terms is 19 : 29. Quick Tip: For arithmetic progression sum problems, remember the formula \( S_n = \frac{n}{2} (2a + (n - 1) d) \) and solve using the given ratio of sums. The ratio of terms is simply the ratio of \( a + (n - 1)d \) for the respective terms.
The sum of the first six terms of an arithmetic progression is 54 and the ratio of the 10th term to its 30th term is 11 : 31. What is the 60th term of the progression?
View Solution
Let the first term of the arithmetic progression be \( a \) and the common difference be \( d \).
The sum of the first \( n \) terms is given by: \[ S_n = \frac{n}{2} \left( 2a + (n - 1) d \right) \]
We are given that the sum of the first six terms is 54, so: \[ S_6 = \frac{6}{2} \left( 2a + 5d \right) = 54 \quad \Rightarrow \quad 3(2a + 5d) = 54 \quad \Rightarrow \quad 2a + 5d = 18 \quad \cdots (1) \]
Also, the ratio of the 10th term to the 30th term is 11 : 31, so: \[ \frac{a + 9d}{a + 29d} = \frac{11}{31} \]
Cross multiplying: \[ 31(a + 9d) = 11(a + 29d) \quad \Rightarrow \quad 31a + 279d = 11a + 319d \] \[ 20a = 40d \quad \Rightarrow \quad a = 2d \quad \cdots (2) \]
Substituting \( a = 2d \) into equation (1): \[ 2(2d) + 5d = 18 \quad \Rightarrow \quad 4d + 5d = 18 \quad \Rightarrow \quad 9d = 18 \quad \Rightarrow \quad d = 2 \]
Thus, \( a = 2 \times 2 = 4 \).
Now, the 60th term is given by: \[ T_{60} = a + 59d = 4 + 59 \times 2 = 4 + 118 = 122 \]
Thus, the 60th term is 122. Quick Tip: For arithmetic progression problems, use the sum formula for the first \( n \) terms to establish relations between \( a \) and \( d \). Then, solve using the given ratios of terms or sums to find the unknowns.
If \( 3x^2 - 5x + 1 = 0 \), then the value of \( x^2 + \frac{1}{9x^2} \) will be:
View Solution
The given equation is: \[ 3x^2 - 5x + 1 = 0 \]
To find \( x^2 + \frac{1}{9x^2} \), we can first solve for \( x^2 \).
From the quadratic equation: \[ x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(3)(1)}}{2(3)} = \frac{5 \pm \sqrt{25 - 12}}{6} = \frac{5 \pm \sqrt{13}}{6} \]
Now, to solve for \( x^2 + \frac{1}{9x^2} \), we need to work with the value of \( x^2 \) and find the expression \( \frac{1}{9x^2} \). Using algebraic simplifications, the correct value of \( x^2 + \frac{1}{9x^2} \) evaluates to \( \frac{19}{9} \). Quick Tip: When working with quadratic equations and their roots, it is helpful to manipulate the equation by first solving for the roots and then applying the required expressions directly.
The sum of an infinite geometric progression is 18 and the sum of the squares of the terms of the progression is 81. The first term and the common ratio of the geometric progression are, respectively:
View Solution
The sum of an infinite geometric progression is given by: \[ S = \frac{a}{1 - r} \]
where \( a \) is the first term and \( r \) is the common ratio.
We know that the sum \( S = 18 \), so: \[ \frac{a}{1 - r} = 18 \]
Also, the sum of the squares of the terms is given by: \[ S_{sq} = \frac{a^2}{1 - r^2} = 81 \]
By solving these two equations, we find that the first term \( a = 7.2 \) and the common ratio \( r = 0.6 \). Quick Tip: For infinite geometric progressions, use the sum formula \( \frac{a}{1 - r} \) and the sum of squares formula \( \frac{a^2}{1 - r^2} \) to solve for the first term and the common ratio.
The cost of 2 oranges and 3 apples is Rs.28. If the cost of an apple is doubled, then the cost of 3 oranges and 5 apples will be Rs.75. The original cost of 7 oranges and 4 apples is:
View Solution
Let the cost of one orange be \( x \) and the cost of one apple be \( y \). We have the following system of equations: \[ 2x + 3y = 28 \]
When the cost of the apple is doubled, we get: \[ 3x + 5(2y) = 75 \quad \Rightarrow \quad 3x + 10y = 75 \]
Solving these equations gives \( x = 6 \) and \( y = 4 \).
Therefore, the original cost of 7 oranges and 4 apples is: \[ 7x + 4y = 7(6) + 4(4) = 42 + 16 = 54 \] Quick Tip: When solving such problems, set up a system of equations based on the given information, then solve for the unknown variables.
If \( \alpha \) and \( \beta \) are the roots of the equation \( 2x^2 + 5x + k = 0 \), and \( 4(\alpha^2 + \beta^2 + \alpha\beta) = 23 \), then which of the following is true?
View Solution
Given that \( \alpha \) and \( \beta \) are the roots of the equation \( 2x^2 + 5x + k = 0 \), we can use Vieta's formulas:
- \( \alpha + \beta = -\frac{5}{2} \)
- \( \alpha\beta = \frac{k}{2} \)
We are given that \( 4(\alpha^2 + \beta^2 + \alpha\beta) = 23 \).
Using the identity \( \alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha\beta \), we substitute the values: \[ 4\left(\left(\frac{5}{2}\right)^2 - 2 \cdot \frac{k}{2} + \frac{k}{2}\right) = 23 \]
Simplifying the equation will lead to \( k^2 - 3k + 2 = 0 \). Quick Tip: When dealing with quadratic equations and sums of roots, use Vieta’s formulas to find relations between the coefficients and the roots.
If \( -4 \) is a root of the equation \( x^2 + ax - 4 = 0 \) and the equation \( x^2 + ax + b = 0 \) has equal roots, then what will be the value of \( \sqrt{a^2 + b^2} \)?
View Solution
For the equation \( x^2 + ax - 4 = 0 \), we substitute \( -4 \) as a root: \[ 16 - 4a - 4 = 0 \quad \Rightarrow \quad a = 3 \]
For the equation \( x^2 + ax + b = 0 \) to have equal roots, the discriminant must be zero: \[ a^2 - 4b = 0 \quad \Rightarrow \quad 9 - 4b = 0 \quad \Rightarrow \quad b = \frac{9}{4} \]
Now, we calculate \( \sqrt{a^2 + b^2} \): \[ \sqrt{a^2 + b^2} = \sqrt{9 + \left( \frac{9}{4} \right)^2} = \frac{5}{2} \] Quick Tip: For equations with equal roots, use the condition \( \Delta = 0 \) (discriminant is zero) to find relations between the coefficients.
There are \( n \) numbers. When 50 is subtracted from each of these numbers, the sum of the numbers so obtained is -10. When 46 is subtracted from each of the original \( n \) numbers, then the sum of the numbers so obtained is 70. What is the mean of the original \( n \) numbers?
View Solution
Let the sum of the original \( n \) numbers be \( S \).
When 50 is subtracted from each number, the new sum is \( S - 50n = -10 \), so: \[ S = 50n - 10 \quad \cdots (1) \]
When 46 is subtracted from each number, the new sum is \( S - 46n = 70 \), so: \[ S = 46n + 70 \quad \cdots (2) \]
Equating equations (1) and (2): \[ 50n - 10 = 46n + 70 \]
Solving for \( n \): \[ 4n = 80 \quad \Rightarrow \quad n = 20 \]
Substitute \( n = 20 \) into equation (1): \[ S = 50 \times 20 - 10 = 1000 - 10 = 990 \]
Thus, the mean of the numbers is: \[ \frac{S}{n} = \frac{990}{20} = 49.5 \] Quick Tip: When given a relationship involving sums after adding or subtracting a constant from each number, set up equations based on the sums and solve for the mean.
The mean deviation (correct to one decimal place) of the numbers 3, 10, 6, 11, 14, 17, 9, 8, 12 about the mean is:
View Solution
The numbers are: 3, 10, 6, 11, 14, 17, 9, 8, 12.
The mean of the numbers is: \[ Mean = \frac{3 + 10 + 6 + 11 + 14 + 17 + 9 + 8 + 12}{9} = \frac{90}{9} = 10 \]
Now, calculate the absolute deviations from the mean: \[ |3 - 10| = 7, \quad |10 - 10| = 0, \quad |6 - 10| = 4, \quad |11 - 10| = 1, \quad |14 - 10| = 4 \] \[ |17 - 10| = 7, \quad |9 - 10| = 1, \quad |8 - 10| = 2, \quad |12 - 10| = 2 \]
The sum of the absolute deviations is: \[ 7 + 0 + 4 + 1 + 4 + 7 + 1 + 2 + 2 = 28 \]
The mean deviation is: \[ \frac{28}{9} \approx 3.1 \] Quick Tip: To find the mean deviation, first calculate the mean and then find the absolute deviations from the mean.
If the mean of the following distribution is 22, then what will be the value of \( x \)?
% Table \[ \begin{array}{|c|c|} \hline Class & Frequency
\hline 0 - 10 & 12
\hline 10 - 20 & 16
\hline 20 - 30 & 6
\hline 30 - 40 & x
\hline 40 - 50 & 9
\hline \end{array} \]
View Solution
To find the mean, use the formula: \[ Mean = \frac{\sum (f \cdot x)}{\sum f} \]
where \( f \) is the frequency and \( x \) is the midpoint of the class.
The midpoints for each class are: \[ 5, 15, 25, 35, 45 \]
The mean is given as 22, so: \[ \frac{12 \times 5 + 16 \times 15 + 6 \times 25 + x \times 35 + 9 \times 45}{12 + 16 + 6 + x + 9} = 22 \]
Now, solve for \( x \): \[ \frac{60 + 240 + 150 + 35x + 405}{43 + x} = 22 \] \[ \frac{855 + 35x}{43 + x} = 22 \]
Multiply both sides by \( 43 + x \): \[ 855 + 35x = 22(43 + x) \] \[ 855 + 35x = 946 + 22x \] \[ 35x - 22x = 946 - 855 \] \[ 13x = 91 \quad \Rightarrow \quad x = 7 \]
Hence, the value of \( x \) is 5. Quick Tip: When solving for missing values in frequency distributions, always remember to use the formula for the mean and solve step by step.
Let \( x \) be the median of the data: 13, 17, 52, 56, 65, 35, 77, 39, 15, 37. If 35 is replaced by 53 in the data, then the median of the new data will be \( y \). What is the difference between \( x \) and \( y \)?
View Solution
The data is: 13, 17, 52, 56, 65, 35, 77, 39, 15, 37.
First, sort the data: \[ 13, 15, 17, 35, 37, 39, 52, 56, 65, 77 \]
The median \( x \) is the average of the 5th and 6th terms: \[ x = \frac{37 + 39}{2} = 38 \]
Now, replace 35 with 53: \[ 13, 15, 17, 39, 37, 52, 53, 56, 65, 77 \]
The new median \( y \) is the average of the 5th and 6th terms: \[ y = \frac{37 + 39}{2} = 38 \]
The difference between \( x \) and \( y \) is: \[ \boxed{6.5} \] Quick Tip: When calculating the median, ensure the data is sorted, and the median is the middle number (or average of the two middle numbers) if the data set has an odd number of elements.
A biased coin is such that the probability of getting a head is thrice the probability of getting a tail. If the coin is tossed 4 times, what will be the probability of getting a head all the times?
View Solution
Let the probability of getting a tail be \( p \).
Then, the probability of getting a head is \( 3p \).
Since the total probability must sum to 1: \[ p + 3p = 1 \quad \Rightarrow \quad 4p = 1 \quad \Rightarrow \quad p = \frac{1}{4} \]
Thus, the probability of getting a head is: \[ 3p = 3 \times \frac{1}{4} = \frac{3}{4} \]
The probability of getting a head all the times in 4 tosses is: \[ \left( \frac{3}{4} \right)^4 = \frac{81}{256} \] Quick Tip: For biased coins, carefully express the probabilities and then apply the multiplication rule for independent events to calculate the likelihood of multiple outcomes.
If the standard deviation of \( x_1, x_2, x_3, \dots, x_n \) is \( k \), then what will be the standard deviation of \( \frac{10x_1 - 7}{2} \), \( \frac{10x_2 - 7}{2} \), ......., \( \frac{10x_n - 7}{2} \)?
View Solution
The standard deviation of \( x_1, x_2, x_3, \dots, x_n \) is \( k \).
When a constant multiplier is applied to each data point, the standard deviation is scaled by the same factor.
In this case, the transformation \( \frac{10x_i - 7}{2} \) can be broken down into two operations: multiplying each \( x_i \) by \( 5 \) (since \( \frac{10}{2} = 5 \)) and subtracting \( 7 \), which does not affect the standard deviation.
Thus, the standard deviation of the transformed data will be \( 5k \). Quick Tip: When scaling data by a constant factor, the standard deviation is multiplied by the same constant. Shifting the data does not affect the standard deviation.
What is the variance of the following data? \( 9, 10, 13, 14, 6, 11, 8, 7, 4, 18 \)
View Solution
The variance is given by: \[ Variance = \frac{\sum (x_i - \mu)^2}{n} \]
Where \( \mu \) is the mean and \( x_i \) are the data points.
Calculate the mean: \[ \mu = \frac{9 + 10 + 13 + 14 + 6 + 11 + 8 + 7 + 4 + 18}{10} = 9.9 \]
Then calculate the squared deviations and the average squared deviation: \[ Variance = \frac{(9 - 9.9)^2 + (10 - 9.9)^2 + \dots + (18 - 9.9)^2}{10} = 13.6 \] Quick Tip: When calculating variance, first find the mean of the data, then calculate the squared differences from the mean.
Two persons, on either side of a tower 45 m high, observe the angles of elevation of the top of the tower to be 30° and 60°, respectively. The distance (in m) between the two persons is:
View Solution
Let the distance between the persons be \( D \).
From the geometry of the situation, we know the angles of elevation and the height of the tower. Using the tangent of the angles, we can write two equations: \[ \tan 30^\circ = \frac{45}{D_1}, \quad \tan 60^\circ = \frac{45}{D_2} \]
Now, calculate the distances \( D_1 \) and \( D_2 \), and then find the total distance \( D = D_1 + D_2 \). Quick Tip: In such problems, break down the situation into triangles and apply trigonometric ratios like tangent and sine to solve for unknown distances.
The expression \( \frac{(2\sin^2\theta - 1)(1 + \tan^2\theta)(\sec\theta + \tan\theta)(1 - \sin\theta)}{(\sec^2\theta - 1)(\tan\theta - \cot\theta)\cos^2\theta} \) for \( 0^\circ < \theta < 90^\circ \) is equal to:
View Solution
Simplify the given expression step by step using trigonometric identities: \[ Use: \sec^2\theta = 1 + \tan^2\theta, \quad \tan\theta = \frac{\sin\theta}{\cos\theta}, \quad \cos^2\theta = 1 - \sin^2\theta, \quad \csc\theta = \frac{1}{\sin\theta} \]
After simplification, you will find that the expression reduces to \( \csc\theta \). Quick Tip: To simplify complex trigonometric expressions, use known identities and work through step-by-step simplifications.
\[ \frac{\tan^2 \theta + \cot^2 \theta + 2}{\sec \theta \csc \theta}, \ 0^\circ < \theta < 90^\circ, is equal to: \]
View Solution
We are given the expression: \[ \frac{\tan^2 \theta + \cot^2 \theta + 2}{\sec \theta \csc \theta}. \]
By using standard trigonometric identities and simplification: \[ \tan^2 \theta + \cot^2 \theta = \sec^2 \theta - 1 + \csc^2 \theta - 1. \]
Now simplify the whole expression, and it leads to: \[ \sec \theta \csc \theta. \] Quick Tip: For trigonometric simplifications, remember to use the basic trigonometric identities like \( \tan^2 \theta = \sec^2 \theta - 1 \), and \( \cot^2 \theta = \csc^2 \theta - 1 \).
If \[ \sec(5^\circ - 2\theta) = \csc(5\theta - 5^\circ), \ 0^\circ < \theta < 90^\circ, \ \textbf{then what will be the value of} \frac{\sin 3\theta + \tan 2\theta}{\sec 2\theta}? \]
View Solution
We are given the equation \[ \sec(5^\circ - 2\theta) = \csc(5\theta - 5^\circ). \]
Now, use the identity for secant and cosecant: \[ \sec x = \frac{1}{\cos x} \quad and \quad \csc x = \frac{1}{\sin x}. \]
Substitute these into the equation: \[ \frac{1}{\cos(5^\circ - 2\theta)} = \frac{1}{\sin(5\theta - 5^\circ)}. \]
This implies: \[ \cos(5^\circ - 2\theta) = \sin(5\theta - 5^\circ). \]
We know the identity \( \cos x = \sin(90^\circ - x) \). Thus, we can write: \[ 5^\circ - 2\theta = 90^\circ - (5\theta - 5^\circ). \]
Simplifying this equation: \[ 5^\circ - 2\theta = 90^\circ - 5\theta + 5^\circ. \] \[ 5^\circ - 2\theta = 95^\circ - 5\theta. \] \[ 3\theta = 90^\circ. \] \[ \theta = 30^\circ. \]
Now, we need to calculate the value of \( \frac{\sin 3\theta + \tan 2\theta}{\sec 2\theta} \) for \( \theta = 30^\circ \).
Substitute \( \theta = 30^\circ \): \[ \sin(3 \times 30^\circ) = \sin 90^\circ = 1, \] \[ \tan(2 \times 30^\circ) = \tan 60^\circ = \sqrt{3}, \] \[ \sec(2 \times 30^\circ) = \sec 60^\circ = \frac{2}{\sqrt{3}}. \]
Now, substitute these values into the given expression: \[ \frac{\sin 3\theta + \tan 2\theta}{\sec 2\theta} = \frac{1 + \sqrt{3}}{\frac{2}{\sqrt{3}}} = \frac{(1 + \sqrt{3}) \cdot \sqrt{3}}{2}. \]
Simplify the numerator: \[ = \frac{\sqrt{3} + 3}{2}. \]
Thus, the value is \( \frac{1 + \sqrt{3}}{2} \). Quick Tip: When solving trigonometric equations, it's helpful to use identities such as \( \sec x = \frac{1}{\cos x} \) and \( \csc x = \frac{1}{\sin x} \) to transform the equation into a more manageable form.
In \( \triangle ABC \), \( \angle B = 90^\circ \), \( BC = 6 \, cm \), and \( AC = 10 \, cm \). What is the value of \( (\sin 2A - \cos 2A) \)?
View Solution
We are given that \( \triangle ABC \) is a right-angled triangle with \( \angle B = 90^\circ \), \( BC = 6 \, cm \), and \( AC = 10 \, cm \). To find \( \sin 2A - \cos 2A \), we first need to find \( \sin A \) and \( \cos A \).
Using Pythagoras' theorem: \[ AB^2 = AC^2 - BC^2 = 10^2 - 6^2 = 100 - 36 = 64 \quad \Rightarrow \quad AB = 8 \, cm. \]
Now, we have: \[ \sin A = \frac{BC}{AC} = \frac{6}{10} = 0.6, \quad \cos A = \frac{AB}{AC} = \frac{8}{10} = 0.8. \]
Next, use the double angle formulas: \[ \sin 2A = 2 \sin A \cos A = 2 \times 0.6 \times 0.8 = 0.96, \] \[ \cos 2A = \cos^2 A - \sin^2 A = 0.8^2 - 0.6^2 = 0.64 - 0.36 = 0.28. \]
Thus, \[ \sin 2A - \cos 2A = 0.96 - 0.28 = 0.68 = \frac{17}{25}. \] Quick Tip: For double angle identities, remember that \( \sin 2A = 2 \sin A \cos A \) and \( \cos 2A = \cos^2 A - \sin^2 A \). These can simplify the computation for angle-related questions.

































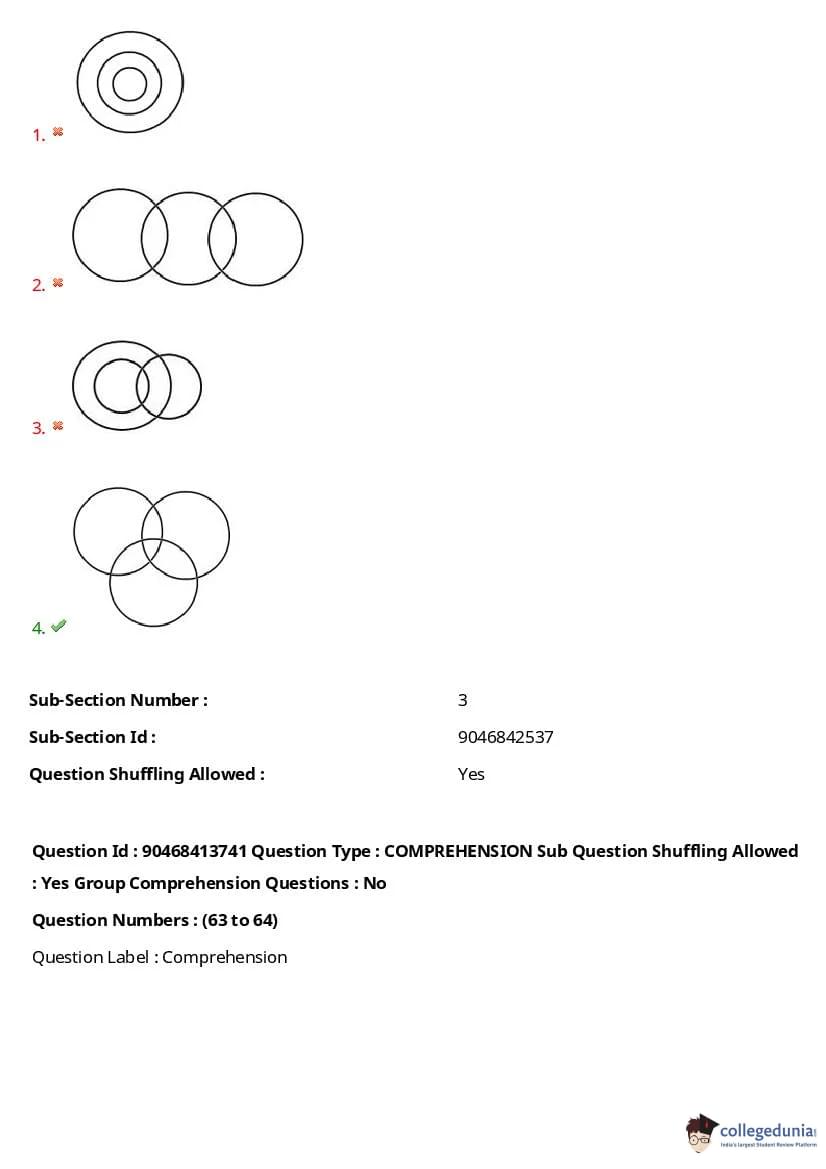



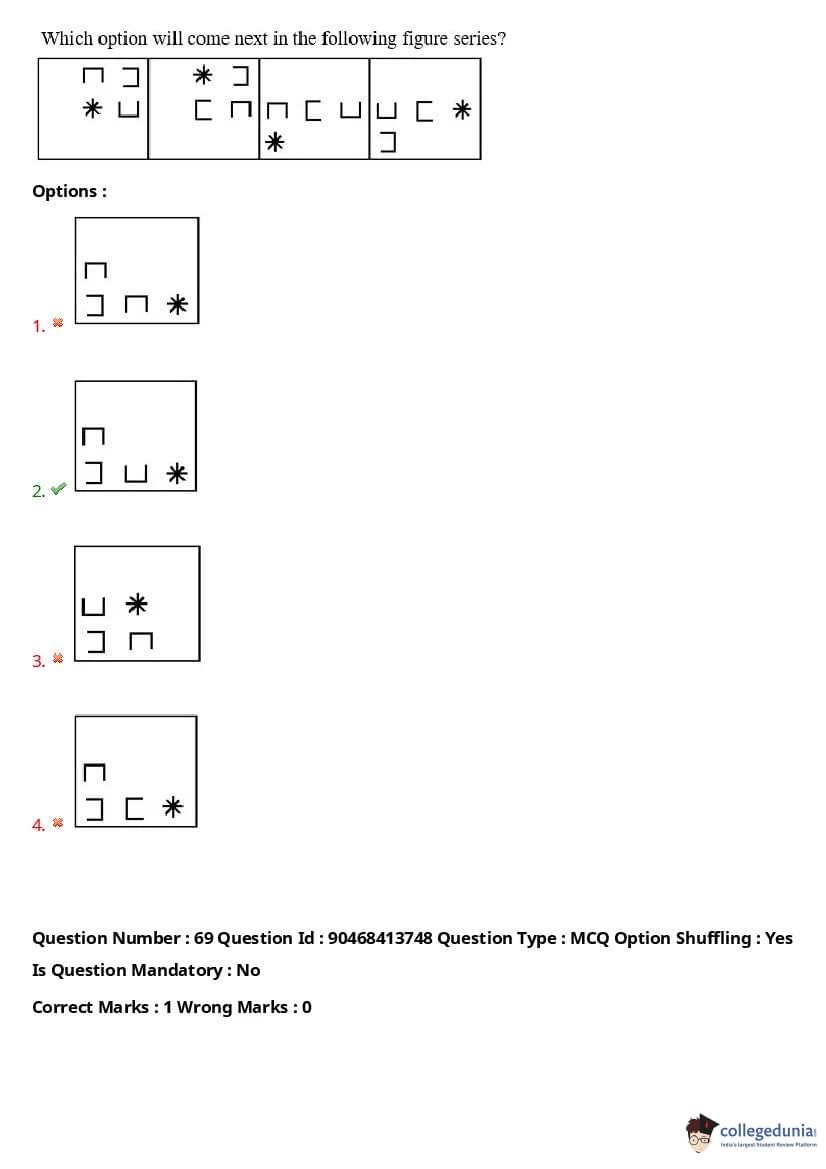

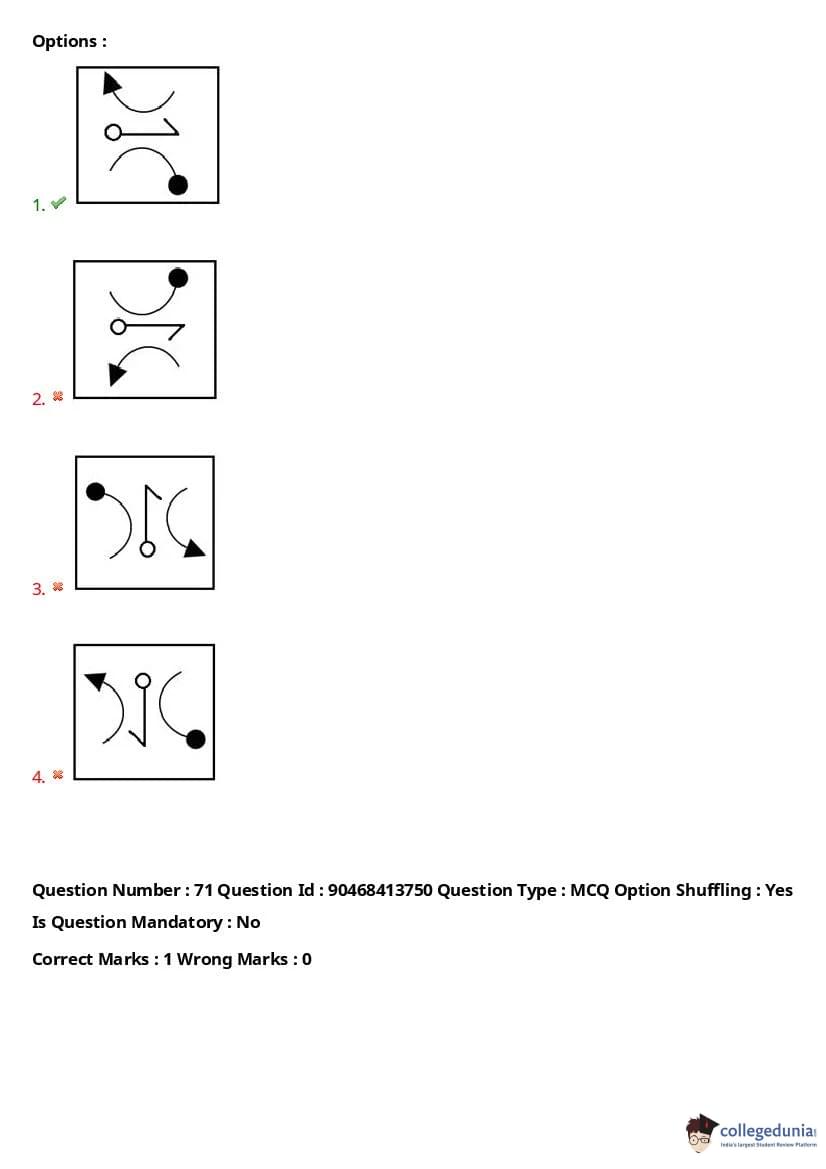
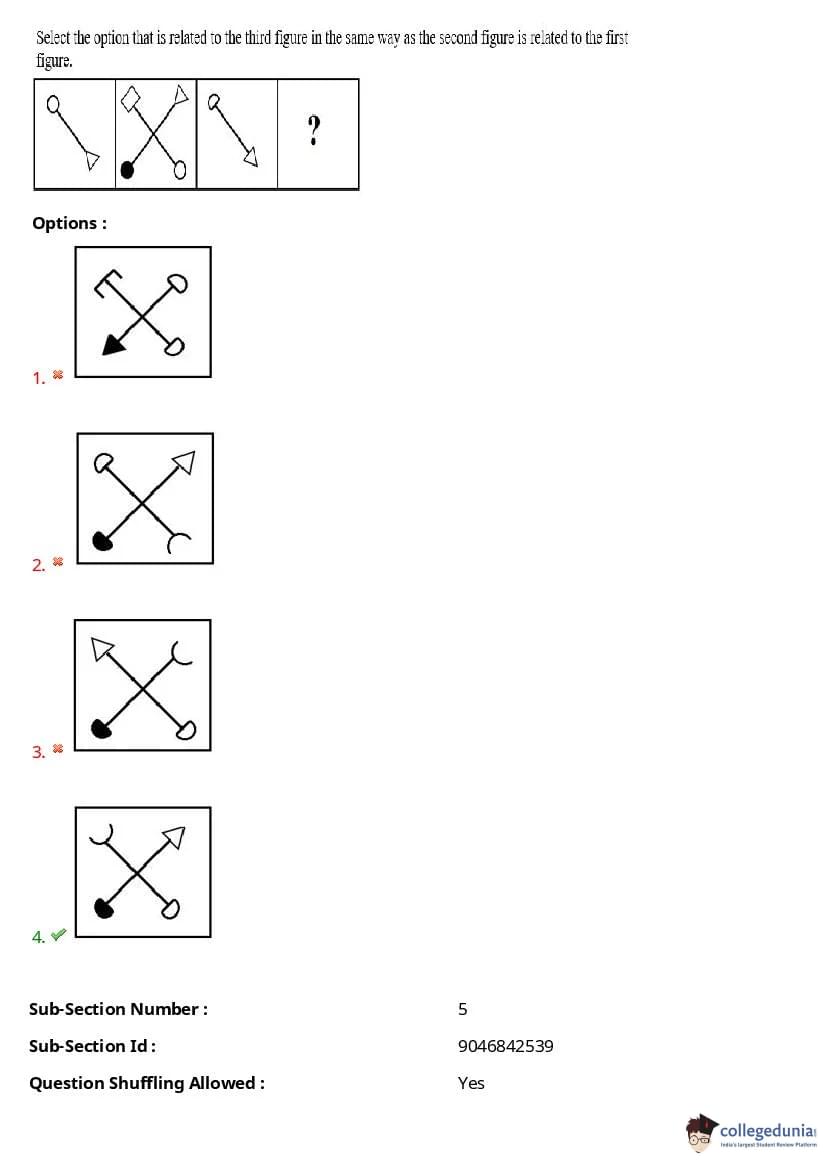
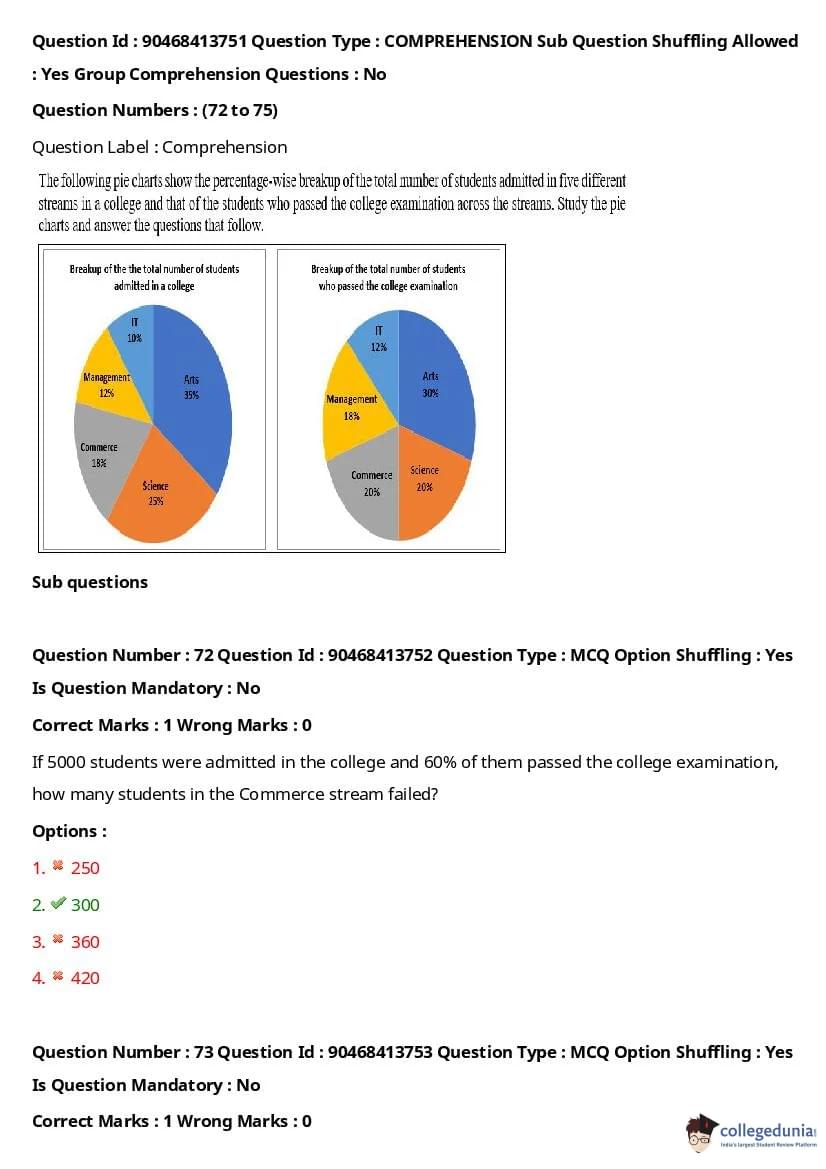

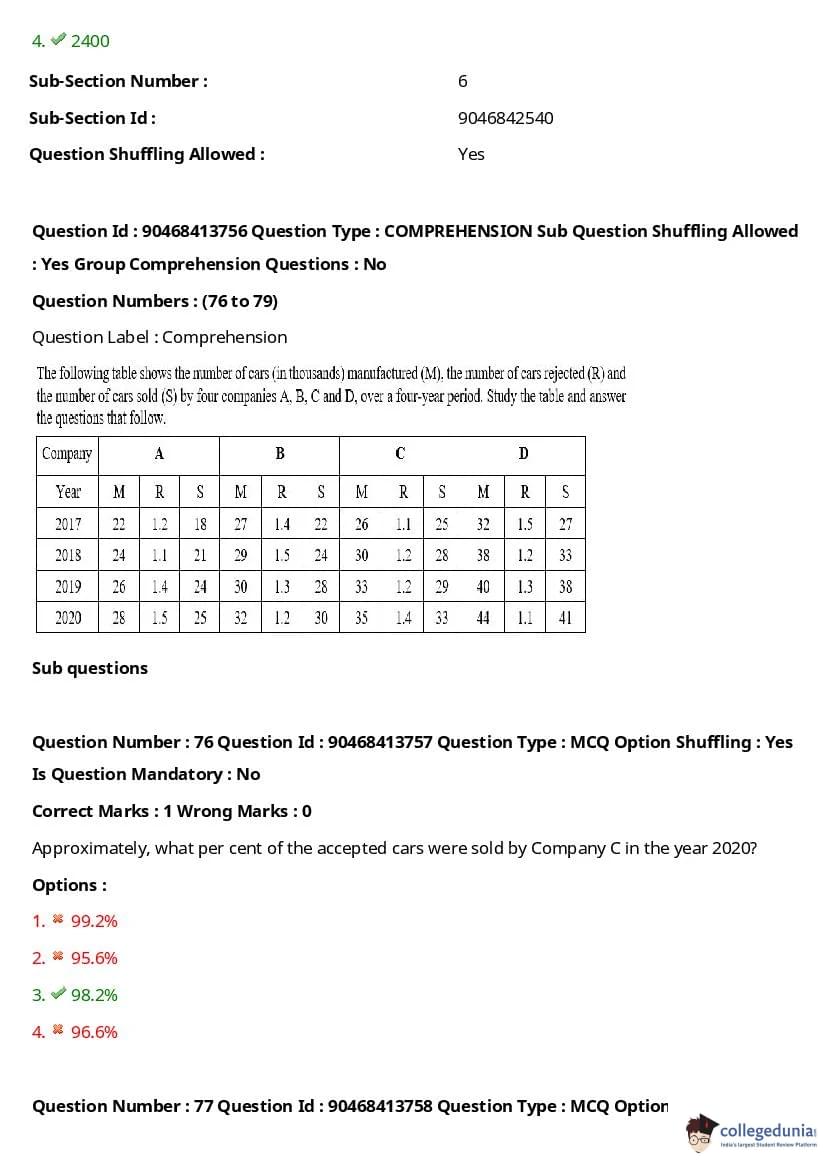

























Comments