Maharashtra Board Class 10 Mathematics (Geometry) Question Paper 2024 with Answer Key pdf is available for download here. The Mathematics paper was conducted on March 13, 2024 in the morning shift from 11:00 AM-2:00 PM. The question paper was divided into two sections - Section A for objective questions and Section B for subjective questions.
| Maharashtra Board Class 10 Mathematics (Geometry) Question Paper With Answer Key | Check Solution |
Maharashtra Board Class 10 Mathematics (Geometry) Question Paper 2024
(1) Out of the dates given below, which date constitutes a Pythagorean triplet?
View Solution
Step 1: A Pythagorean triplet satisfies the condition \( a^2 + b^2 = c^2 \). Let us check the given options:
- For \( 3, 5, 17 \):
\[ 3^2 + 5^2 = 9 + 25 = 34 \neq 17^2. \]
This is incorrect.
- For \( 4, 9, 15 \):
\[ 4^2 + 9^2 = 16 + 81 = 97 \neq 15^2. \]
This is incorrect.
Thus, none of the options form a Pythagorean triplet. Quick Tip: For a Pythagorean triplet, always verify \( a^2 + b^2 = c^2 \). Ensure the largest number is \( c \), the hypotenuse.
Find the value of \( \sin 0 \times \csc 0 \):
View Solution
Step 1: Using the trigonometric identity: \[ \sin x \times \csc x = 1 \quad for all x \neq 0. \]
Substituting \( x = 0 \), we get: \[ \sin 0 \times \csc 0 = 1. \] Quick Tip: The reciprocal identity \( \sin x \times \csc x = 1 \) is always valid for non-zero angles.
What is the slope of the X-axis?
View Solution
Step 1: The X-axis is a horizontal line. The slope of a horizontal line is given by: \[ slope = \frac{\Delta y}{\Delta x} = 0. \] Quick Tip: For horizontal lines (e.g., X-axis), the slope is always \( 0 \). For vertical lines (e.g., Y-axis), the slope is undefined.
A circle having radius \( 3 \, cm \), then the length of its largest chord is:
View Solution
Step 1: The largest chord of a circle is its diameter. The diameter of a circle is given by: \[ Diameter = 2 \times Radius. \]
Step 2: Substituting the given radius \( 3 \, cm \), we find: \[ Diameter = 2 \times 3 = 6 \, cm. \]
Hence, the largest chord is \( 6 \, cm \). Quick Tip: The diameter of a circle is the longest chord, always equal to \( 2 \times Radius \).
(1) If \( \triangle ABC \sim \triangle PQR \) and \( AB : PQ = 2 : 3 \), then find the value of \( \frac{A(\triangle ABC)}{A(\triangle PQR)} \):
View Solution
Step 1: For two similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides: \[ \frac{A(\triangle ABC)}{A(\triangle PQR)} = \left(\frac{AB}{PQ}\right)^2. \]
Step 2: Substituting \( AB : PQ = 2 : 3 \): \[ \frac{A(\triangle ABC)}{A(\triangle PQR)} = \left(\frac{2}{3}\right)^2 = \frac{4}{9}. \] Quick Tip: For similar triangles, the area ratio is the square of the ratio of corresponding sides.
Two circles of radii \( 5 \, cm \) and \( 3 \, cm \) touch each other externally. Find the distance between their centres.
View Solution
Step 1: If two circles touch externally, the distance between their centres is equal to the sum of their radii: \[ Distance = R_1 + R_2. \]
Step 2: Substituting \( R_1 = 5 \, cm \) and \( R_2 = 3 \, cm \): \[ Distance = 5 + 3 = 8 \, cm. \] Quick Tip: For externally touching circles, the distance between their centres equals the sum of their radii.
Find the side of a square whose diagonal is \( 10\sqrt{2} \, cm \):
View Solution
Step 1: The diagonal \( d \) of a square relates to its side \( a \) by: \[ d = a\sqrt{2}. \]
Step 2: Substituting \( d = 10\sqrt{2} \, cm \): \[ 10\sqrt{2} = a\sqrt{2}. \]
Step 3: Dividing both sides by \( \sqrt{2} \): \[ a = 10 \, cm. \] Quick Tip: The diagonal of a square is always \( \sqrt{2} \) times the length of its side.
A line makes an angle of \( 45^\circ \) with the positive direction of the X-axis. Find the slope of the line.
View Solution
Step 1: The slope of a line is given by: \[ Slope = \tan \theta, \]
where \( \theta \) is the angle made with the positive X-axis.
Step 2: Substituting \( \theta = 45^\circ \): \[ Slope = \tan 45^\circ = 1. \] Quick Tip: The slope of a line at \( 45^\circ \) with the X-axis is always \( 1 \), as \( \tan 45^\circ = 1 \).
(1) In the above figure, \( \triangle ABC \) is inscribed in arc \( ABC \). If \( \angle ABC = 60^\circ \), find \( m\angle AOC \):
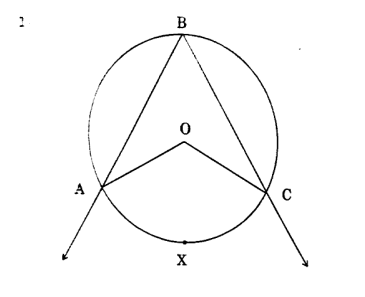
View Solution
Step 1: Using the property of inscribed angles, the measure of an inscribed angle is half the measure of the arc it subtends: \[ \angle ABC = \frac{1}{2} m(arc AXC). \]
Substituting \( \angle ABC = 60^\circ \): \[ 60^\circ = \frac{1}{2} m(arc AXC). \]
Step 2: Solving for \( m(arc AXC) \): \[ m(arc AXC) = 2 \times 60^\circ = 120^\circ. \]
Step 3: Using the property of central angles, the measure of a central angle is equal to the measure of the arc it subtends: \[ m\angle AOC = m(arc AXC) = 120^\circ. \]
Hence, \( m\angle AOC = 120^\circ \). Quick Tip: For inscribed angles, remember that \( Inscribed Angle = \frac{1}{2} \times Intercepted Arc \). For central angles, \( Central Angle = Intercepted Arc \).
Find the value of \( \sin^2 \theta + \cos^2 \theta \):

View Solution
Step 1: In \( \triangle ABC \), \( \angle ABC = 90^\circ \) and \( \angle C = \theta \). From the Pythagoras theorem: \[ AB^2 + BC^2 = AC^2. \]
Step 2: Dividing throughout by \( AC^2 \): \[ \frac{AB^2}{AC^2} + \frac{BC^2}{AC^2} = \frac{AC^2}{AC^2}. \]
Step 3: Simplifying, we get: \[ \left(\frac{AB}{AC}\right)^2 + \left(\frac{BC}{AC}\right)^2 = 1. \]
Step 4: Substituting trigonometric ratios: \[ \sin \theta = \frac{BC}{AC}, \quad \cos \theta = \frac{AB}{AC}. \]
Thus: \[ \sin^2 \theta + \cos^2 \theta = 1. \] Quick Tip: The Pythagoras theorem is the foundation of the identity \( \sin^2 \theta + \cos^2 \theta = 1 \). Always check for right-angle triangles when applying this formula.
In the figure given above, \( ABCD \) is a square, and a circle is inscribed in it. All sides of the square touch the circle. If \( AB = 14 \, cm \), find the area of the shaded region.

View Solution
Step 1: The area of the square is given by: \[ Area of square = (side)^2. \]
Substituting \( side = 14 \, cm \): \[ Area of square = 14^2 = 196 \, cm^2. \]
Step 2: The area of the circle is given by: \[ Area of circle = \pi r^2. \]
Here, the diameter of the circle is equal to the side of the square, so the radius \( r = \frac{14}{2} = 7 \, cm \). Substituting \( r = 7 \): \[ Area of circle = \frac{22}{7} \times 7 \times 7 = 154 \, cm^2. \]
Step 3: The area of the shaded region is the difference between the area of the square and the area of the circle: \[ Area of shaded region = Area of square - Area of circle. \]
Substituting the values: \[ Area of shaded region = 196 - 154 = 42 \, cm^2. \] Quick Tip: When a circle is inscribed in a square, the diameter of the circle equals the side length of the square. Use this relationship to compute the radius of the circle.
(1) Radius of a sector of a circle is \( 3.5 \, cm \) and length of its arc is \( 2.2 \, cm \). Find the area of the sector.
View Solution
Step 1: The area of the sector is given by: \[ Area of sector = \frac{1}{2} \times r \times arc length. \]
Step 2: Substituting \( r = 3.5 \, cm \) and \( arc length = 2.2 \, cm \): \[ Area of sector = \frac{1}{2} \times 3.5 \times 2.2 = 3.85 \, cm^2. \] Quick Tip: To calculate the area of a sector, use \( Area = \frac{1}{2} \times r \times arc length \) directly if the arc length is given.
Find the length of the hypotenuse of a right-angled triangle if the remaining sides are \( 9 \, cm \) and \( 12 \, cm \).
View Solution
Step 1: Using the Pythagoras theorem: \[ Hypotenuse^2 = Side_1^2 + Side_2^2. \]
Step 2: Substituting \( Side_1 = 9 \, cm \) and \( Side_2 = 12 \, cm \): \[ Hypotenuse^2 = 9^2 + 12^2 = 81 + 144 = 225. \]
Step 3: Taking the square root: \[ Hypotenuse = \sqrt{225} = 15 \, cm. \] Quick Tip: For right triangles, always apply the Pythagoras theorem: \( c^2 = a^2 + b^2 \).
In the figure below, \( m(arc NS) = 125^\circ \), \( m(arc EF) = 37^\circ \). Find the measure of \( \angle NMS \).

View Solution
Step 1: The measure of the angle \( \angle NMS \) is equal to half the difference of the measures of the intercepted arcs: \[ \angle NMS = \frac{1}{2} \left[ m(arc NS) - m(arc EF) \right]. \]
Step 2: Substituting \( m(arc NS) = 125^\circ \) and \( m(arc EF) = 37^\circ \): \[ \angle NMS = \frac{1}{2} \left( 125^\circ - 37^\circ \right) = \frac{1}{2} \times 88^\circ = 44^\circ. \] Quick Tip: For angles formed by two secants, use the formula: \( Angle = \frac{1}{2} (larger arc - smaller arc) \).
Find the slope of the line passing through the points \( A(2, 3) \) and \( B(4, 7) \).
View Solution
Step 1: The slope of a line passing through two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is given by: \[ m = \frac{y_2 - y_1}{x_2 - x_1}. \]
Step 2: Substituting \( (x_1, y_1) = (2, 3) \) and \( (x_2, y_2) = (4, 7) \): \[ m = \frac{7 - 3}{4 - 2} = \frac{4}{2} = 2. \] Quick Tip: For slope, remember the formula \( m = \frac{y_2 - y_1}{x_2 - x_1} \) and ensure you correctly subtract coordinates.
Find the surface area of a sphere of radius \( 7 \, cm \).
View Solution
Step 1: The surface area of a sphere is given by: \[ Surface area = 4\pi r^2. \]
Step 2: Substituting \( r = 7 \, cm \): \[ Surface area = 4 \times \frac{22}{7} \times 7^2 = 4 \times \frac{22}{7} \times 49 = 616 \, cm^2. \] Quick Tip: For spheres, the surface area formula is \( 4\pi r^2 \). Substitute \( \pi = \frac{22}{7} \) for approximate calculations.
(1) In \( \triangle ABC \), ray \( BD \) bisects \( \angle ABC \), \( A - D - C \), and \( seg DE \parallel side BC \). If \( A - E - B \), then for showing \( \frac{AB}{BC} = \frac{AE}{EB} \), complete the following activity:
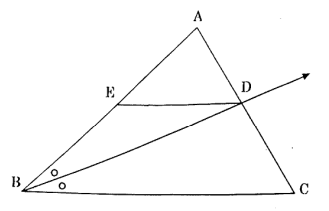
View Solution
N/A Quick Tip: For proving ratios in triangles with parallel lines, use the basic proportionality theorem or the angle bisector theorem effectively.
Given: Chords \( AB \) and \( CD \) of a circle with center \( P \) intersect at point \( E \).
To Prove: \( AE \times EB = CE \times ED \).

View Solution
N/A Quick Tip: For intersecting chords in a circle, use the inscribed angle theorem and properties of similar triangles to establish proportionality and cross-multiplication.
(1) Determine whether the points \( A(1, -3), B(2, -5), C(-4, 7) \) are collinear.
View Solution
Step 1: To determine collinearity, check if the slope of \( AB \) is equal to the slope of \( BC \).
Step 2: Slope of \( AB \): \[ m_{AB} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-5 - (-3)}{2 - 1} = \frac{-5 + 3}{1} = -2. \]
Step 3: Slope of \( BC \): \[ m_{BC} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{7 - (-5)}{-4 - 2} = \frac{7 + 5}{-6} = \frac{12}{-6} = -2. \]
Step 4: Since \( m_{AB} = m_{BC} \), the points are collinear. Quick Tip: To check for collinearity, verify if the slopes of the line segments between the points are equal.
\( \triangle ABC \sim \triangle LMN \). In \( \triangle ABC \), \( AB = 5.5 \, cm \), \( BC = 6 \, cm \), \( CA = 4.5 \, cm \). Construct \( \triangle ABC \) and \( \triangle LMN \) such that \( \frac{BC}{MN} = \frac{5}{4} \).
View Solution
Step 1: Construct \( \triangle ABC \):
Draw a base \( BC = 6 \, cm \).
At point \( B \), construct \( \angle ABC \) using a protractor such that \( AB = 5.5 \, cm \).
At point \( C \), construct \( \angle ACB \) using a protractor such that \( CA = 4.5 \, cm \).
Mark the point of intersection of the two arcs as \( A \), and join \( AB \) and \( AC \) to complete \( \triangle ABC \).
Step 2: Construct \( \triangle LMN \) similar to \( \triangle ABC \) with a scale factor of \( \frac{4}{5} \):
Draw a base \( MN \) such that \( MN = \frac{4}{5} \times BC = \frac{4}{5} \times 6 = 4.8 \, cm \).
At point \( M \), construct an angle equal to \( \angle ABC \).
At point \( N \), construct an angle equal to \( \angle ACB \).
Mark the point of intersection of the two arcs as \( L \), and join \( LM \) and \( LN \) to complete \( \triangle LMN \).
Step 3: Verify similarity: \[ \frac{AB}{LM} = \frac{BC}{MN} = \frac{CA}{LN} = \frac{5}{4}. \] Quick Tip: For constructing similar triangles, ensure that the scale factor is applied consistently to all sides, and corresponding angles are preserved.
Segment \( PM \) is a median of \( \triangle PQR \), \( PM = 9 \), and \( PQ^2 + PR^2 = 290 \). Find \( QR \).
View Solution
Step 1: Using the Apollonius theorem for medians in a triangle: \[ PQ^2 + PR^2 = 2PM^2 + \frac{1}{2}QR^2. \]
Step 2: Substituting the given values \( PQ^2 + PR^2 = 290 \), \( PM = 9 \): \[ 290 = 2(9^2) + \frac{1}{2}QR^2. \]
Step 3: Simplify: \[ 290 = 2(81) + \frac{1}{2}QR^2. \]
\[ 290 = 162 + \frac{1}{2}QR^2. \]
Step 4: Rearrange and solve for \( QR^2 \): \[ 290 - 162 = \frac{1}{2}QR^2. \]
\[ 128 = \frac{1}{2}QR^2 \quad \Rightarrow \quad QR^2 = 256. \]
Step 5: Taking the square root: \[ QR = \sqrt{256} = 16. \] Quick Tip: The Apollonius theorem is useful for finding side lengths in triangles when medians are involved.
Prove that, "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points, then the line divides the sides in the same proportion."
View Solution
Step 1: Consider \( \triangle ABC \) with a line \( DE \parallel BC \) intersecting \( AB \) at \( D \) and \( AC \) at \( E \).
Step 2: In \( \triangle ADE \) and \( \triangle ABC \), since \( DE \parallel BC \), corresponding angles are equal: \[ \angle ADE = \angle ABC, \quad \angle DEA = \angle BCA. \]
Step 3: By AA similarity criterion: \[ \triangle ADE \sim \triangle ABC. \]
Step 4: From the similarity property: \[ \frac{AD}{DB} = \frac{AE}{EC}. \]
Step 5: This proves that the line \( DE \) divides the sides \( AB \) and \( AC \) in the same proportion. Quick Tip: The basic proportionality theorem (Thales' theorem) is a fundamental result for parallel lines in triangles.
Question 4:
Solve any two of the following sub-questions:
\( \frac{1}{\sin^2 \theta} - \frac{1}{\cos^2 \theta} - \frac{1}{\tan^2 \theta} - \frac{1}{\cot^2 \theta} - \frac{1}{\sec^2 \theta} - \frac{1}{\csc^2 \theta} = -3 \), then find the value of \( \theta \).
View Solution
Step 1: Rewrite the given expression using trigonometric identities: \[ \frac{1}{\sin^2 \theta} = \csc^2 \theta, \quad \frac{1}{\cos^2 \theta} = \sec^2 \theta, \quad \frac{1}{\tan^2 \theta} = \cot^2 \theta. \]
Substituting these identities: \[ \csc^2 \theta - \sec^2 \theta - \cot^2 \theta - \tan^2 \theta - \sec^2 \theta - \csc^2 \theta = -3. \]
Step 2: Simplify: \[ -\sec^2 \theta - \sec^2 \theta - \cot^2 \theta - \tan^2 \theta = -3. \]
Step 3: Use the Pythagorean identities: \[ \sec^2 \theta = \tan^2 \theta + 1, \quad \csc^2 \theta = \cot^2 \theta + 1. \]
Solving the equation, \( \theta = 45^\circ \). Quick Tip: For such problems, use reciprocal and Pythagorean identities effectively to simplify the expressions.
(1) \( ABCD \) is a trapezium, \( AB \parallel CD \), and the diagonals of the trapezium intersect at point \( P \). Write the answers to the following questions:
[(a)] Draw the figure using the given information.
[(b)] Write any one pair of alternate angles and opposite angles.
[(c)] Write the names of similar triangles with a test of similarity.
View Solution
(a) Drawing the figure:
The figure is shown above, where \( AB \parallel CD \), and the diagonals \( AC \) and \( BD \) intersect at \( P \).
(b) Alternate and opposite angles:
One pair of alternate angles: \[ \angle APD = \angle CPB. \]
One pair of opposite angles: \[ \angle APB = \angle CPD. \]
(c) Names of similar triangles:
The triangles \( \triangle APB \) and \( \triangle CPD \) are similar by the AA similarity test: \[ \angle APB = \angle CPD \quad and \quad \angle PAB = \angle PCD. \] Quick Tip: In a trapezium, diagonals often form similar triangles by the AA similarity criterion due to parallel sides and corresponding angles.
(2) \( AB \) is a chord of a circle with center \( O \), \( AOC \) is the diameter of the circle, and \( AT \) is a tangent at \( A \). Write the answers to the following questions:
[(a)] Draw the figure using the given information.
[(b)] Find the measures of \( \angle CAT \) and \( \angle ABC \) with reasons.
[(c)] Determine whether \( \angle CAT \) and \( \angle ABC \) are congruent. Justify your answer.
View Solution
(a) Drawing the figure:
The figure is shown above, where \( AOC \) is the diameter, \( AB \) is a chord, and \( AT \) is a tangent.
(b) Measures of \( \angle CAT \) and \( \angle ABC \):
\[ \angle CAT = 90^\circ \quad (Tangent-radius property: tangent is perpendicular to the radius at the point of contact). \]
\[ \angle ABC = 90^\circ \quad (Angle subtended by the diameter in a semicircle is a right angle). \]
(c) Congruence of \( \angle CAT \) and \( \angle ABC \):
Yes, \( \angle CAT \) and \( \angle ABC \) are congruent as they are both equal to \( 90^\circ \) by different properties (tangent-radius property and semicircle theorem). Quick Tip: For tangents and diameters in circles, remember that the tangent at a point of contact is perpendicular to the radius, and the angle in a semicircle is always \( 90^\circ \).




Comments