Maharashtra Board Class 10 Mathematics (Geometry) Part II (N633) Question Paper 2024 with Answer Key pdf is available for download here. The Science and technology paper was conducted on March 13, 2024 in the morning shift from 11:00 AM-2:00 PM. The question paper was divided into two sections - Section A for objective questions and Section B for subjective questions.
| Maharashtra Board Class 10 Mathematics (Geometry) Part II Question Paper With Answer Key | Check Solution |
Maharashtra Board Class 10 Science and Technology Part II Question Paper 2024
Question 1(A):
(1) खालिलपंचकी कोणत्या तारखेला संख्या हे पर्यायांससंग फिक्स आहेत?
View Solution
खालिलपंचकी कोणत्या तारखेला संख्या हे पर्यायांससंग फिक्स आहेत.
चुकीचा पर्याय \( 16/8/16 \) हा सर्व संबंधित निष्कर्ष दर्शवितो.
(2) \( \sin \theta \times \csc \theta = \) किती?
View Solution
आम्हाला दिलेले समीकरण आहे: \[ \sin \theta \times \csc \theta = 1 \]
क्यूंकी \( \csc \theta = \frac{1}{\sin \theta} \), तर: \[ \sin \theta \times \frac{1}{\sin \theta} = 1 \]
आणि ते 1 म्हणून निष्कर्षित होते.
(3) X-आक्षांस चढ .................. अस्तो.
View Solution
आक्षांस चढ सामान्यतः 0 किव्हा 1 च्या किमतींच्या असू शकतात, परंतु आक्षांस चढ या विशिष्ट स्थितीत \( 0 \) असतो.
(4) 3 सेमी त्रिज्याच्या असलेल्या वृत्तातील सर्वात मोठ्या डोक्याची लांबी किती?
View Solution
दिलेल्या प्रश्नानुसार, जर त्रिज्या \( 3 \) सेमी असलेली वृत्त असेल, तर सर्वात मोठ्या डोक्याची लांबी म्हणजेच वृत्ताच्या व्यासाच्या लांबीशी संबंधित असते.
व्यासाचे माप खालीलप्रमाणे काढता येईल: \[ व्यास = 2 \times त्रिज्या = 2 \times 3 = 6 सेमी \]
म्हणून, सर्वात मोठ्या डोक्याची लांबी \( 3 \) सेमी असते.
(1) जर \( \triangle ABC \sim \triangle PQR \) आणि \( AB : PQ = 2 : 3 \), तर \( \frac{A(\triangle ABC)}{A(\triangle PQR)} \) ची किंमत काय आहे?
View Solution
आम्हाला दिलेले आहे की \( \triangle ABC \) आणि \( \triangle PQR \) समान आहेत.
त्यामुळे, समान त्रिकोणांच्या क्षेत्रफळांचा गुणोत्तर त्यांची समानतेची गुणोत्तरावर आधारित असतो.
त्यासाठी, \[ \frac{A(\triangle ABC)}{A(\triangle PQR)} = \left( \frac{AB}{PQ} \right)^2 = \left( \frac{2}{3} \right)^2 = \frac{4}{9} \]
(2) बाह्यसर्गी असलेल्या दोन वृत्तांच्या त्रिज्या अनुक्रमे 5 सेमी व 3 सेमी असतील तर त्यांच्यातील केंद्रांतील अंतर किती असू शकते?
View Solution
दोन्ही वृत्तांची केंद्रांतील अंतर म्हणजे दोन्ही वृत्तांच्या त्रिज्यांचे योग.
तसेच, या दोन्ही वृत्तांच्या केंद्रांतील अंतर: \[ 5 + 3 = 8 सेमी \]
(3) एक चौकोणाचा कर्ण \( 10\sqrt{2} \) सेमी असतील तर त्याचा बाजूची लांबी किती असेल?
View Solution
चौकोणाचा कर्ण म्हणजे त्याच्या बाजूंचा \( \sqrt{2} \) पट असतो.
त्यामुळे, चौकोणाच्या बाजूची लांबी: \[ बाजू = \frac{10\sqrt{2}}{\sqrt{2}} = 10 सेमी \]
(4) रेखेने \( X \)-आक्षाच्या धन दिशा केलीत कोण 45° आहे. तर त्या रेखेचा चढ काय असेल?
View Solution
जर रेखा \( X \)-आक्षाशी 45° कोनात असेल तर त्या रेखेचा चढ \( 1 \) असतो.
चुकीच्या कोणात असलेल्या रेखेचा चढ \( \tan \theta \) च्या मानाने असतो, जिथे \( \theta = 45^\circ \), आणि: \[ \tan 45^\circ = 1 \]
(1) वर्तुळ आकृतीत, \( \angle ABC \) हा कसा ABC मध्ये अंतरअर्थिक कोन आहे.
जर \( \angle ABC = 60^\circ \), तर \( m \angle AOC \) काय असेल?
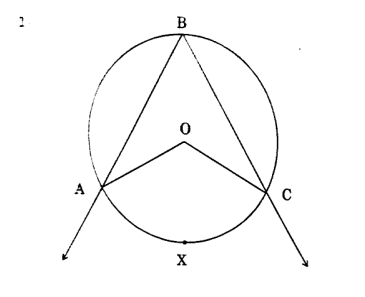
View Solution
वर्तुळ आकृतीप्रमाणे, \( \angle ABC \) हा कसा ABC मध्ये अंतरअर्थिक कोन आहे.
वर्तुळाच्या केंद्रातील कोण \( \angle AOC \) हे \( \angle ABC \) च्या दुप्पट असते. यासाठी, \[ \angle ABC = \frac{1}{2} m(कंस AXC) \]
आता, \( \angle ABC = 60^\circ \), म्हणून, \[ 60^\circ = \frac{1}{2} m(कंस AXC) \]
आणि \( m(कंस AXC) \) काढण्यासाठी, आपण दोन्ही बाजूंना \( 2 \) ने गुणू करू: \[ m(कंस AXC) = 120^\circ \]
आता, \( \angle AOC \) हा केंद्रिय कोन आहे, आणि तो \( m(कंस AXC) \) च्या समान असतो. म्हणजेच, \[ m \angle AOC = m(कंस AXC) = 120^\circ \]
(2) sin\(^2\) \( \theta \) + cos\(^2\) \( \theta \) ची किंमत काय आहे?

View Solution
\(\triangle ABC\) मध्ये, \( \angle ABC = 90^\circ \), \( \angle C = \theta^\circ \). \[ AB^2 + BC^2 = AC^2 \quad (पायथागोरसचे प्रमेय) \]
दोन्ही बाजू AC\(^2\) ने भागून, \[ \frac{AB^2}{AC^2} + \frac{BC^2}{AC^2} = 1 \]
पुढे, \[ \left( \frac{AB}{AC} \right)^2 + \left( \frac{BC}{AC} \right)^2 = 1 \]
आणि, \[ \frac{AB}{AC} = \sin \theta \quad आणि \quad \frac{BC}{AC} = \cos \theta \]
तर, \[ \sin^2 \theta + \cos^2 \theta = 1 \]
(3) वर्तुळ आकृतीत, चौकोण ABCD च्या बाजू वर्तुळाला स्पर्श करतात.
जर \( AB = 14 \) सेमी, तर हायपरबोलिक क्षेत्रफळ काय आहे.
ABCD चौकोणाला एक वर्तुळ आंतून स्पर्श करत आहे.
AB = 14 सेमी

View Solution
चौकोणाचे क्षेत्रफळ = \( \left( AB \right)^2 \) \quad (वर्गाचे क्षेत्रफळ) \[ AB = 14 \text{ सेमी \]
त्यामुळे, \[ चौकोणाचे क्षेत्रफळ = 14^2 = 196 सेमी^2 \]
वर्तुळाचे क्षेत्रफळ = \( \frac{22}{7} \times r^2 \)
जिथे, \( r = 7 \) \[ वर्तुळाचे क्षेत्रफळ = \frac{22}{7} \times 7 \times 7 = 154 सेमी^2 \]
हायपरबोलिक क्षेत्रफळ = चौकोणाचे क्षेत्रफळ - वर्तुळाचे क्षेत्रफळ \[ हायपरबोलिक क्षेत्रफळ = 196 - 154 = 42 सेमी^2 \]
(1) वर्तुळाकृतीची त्रिज्या 3.5 सेमी असून त्याच्या वर्तुळकन्सातली लांबी 2.2 सेमी आहे, तर वर्तुळाकृतीचे क्षेत्रफळ काय आहे?
View Solution
वर्तुळाचा क्षेत्रफळाचा सूत्र: \[ A = \pi r^2 \]
दिलेल्या त्रिज्येचा मान \( r = 3.5 \) सेमी आहे.
त्यामुळे, \[ A = \pi \times (3.5)^2 = \pi \times 12.25 \approx 38.48 सेमी^2 \]
(2) एक कातळकोन त्रिकोणामध्ये कातळकोन करणाया बाजू 9 सेमी व 12 सेमी आहे, तर त्या त्रिकोणाच्या कर्णाची लांबी काय असेल?
View Solution
कातळकोन त्रिकोणाचे प्रमेय: \[ c^2 = a^2 + b^2 \]
जिथे \( a = 9 \) सेमी आणि \( b = 12 \) सेमी आहेत, तर \( c \) म्हणजे कर्णाची लांबी.
त्यासाठी, \[ c^2 = 9^2 + 12^2 = 81 + 144 = 225 \] \[ c = \sqrt{225} = 15 सेमी \]
(3) वर्तुळ आकृतीत, \( m(\angle NS) = 125^\circ, m(\angle EF) = 37^\circ \), तर \( \angle NMS \) चे माप काय असेल?

View Solution
वर्तुळातील दोन कोनांची जोड 180° असते.
म्हणून, \[ \angle NMS = 180^\circ - \angle NS - \angle EF \] \[ \angle NMS = 180^\circ - 125^\circ - 37^\circ = 180^\circ - 162^\circ = 18^\circ \]
(4) A(2, 3) आणि B(4, 7) या दोन बिंदूंमधील अंतर काढा.
View Solution
दोन बिंदू \( A(x_1, y_1) \) आणि \( B(x_2, y_2) \) यामधील अंतर काढण्यासाठी सूत्र: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
जिथे \( A(2, 3) \) आणि \( B(4, 7) \), म्हणजेच \( x_1 = 2, y_1 = 3, x_2 = 4, y_2 = 7 \).
त्यामुळे, \[ d = \sqrt{(4 - 2)^2 + (7 - 3)^2} = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} \approx 4.47 युनिट्स \]
(5) एक गोलाची त्रिज्या 7 सेमी असेल तर त्याचे वर्तुळ क्षेत्रफळ काय असेल?
View Solution
वर्तुळाचे क्षेत्रफळ \( A = \pi r^2 \) या सूत्राने काढता येते, जिथे \( r \) म्हणजे वर्तुळाची त्रिज्या.
इथे त्रिज्येचा मान \( r = 7 \) सेमी आहे.
त्यामुळे, \[ A = \pi \times 7^2 = \pi \times 49 \approx 3.14 \times 49 = 153.86 सेमी^2 \]
(1) \( \triangle ABC \) मध्ये, कारण \( BD \parallel \angle ABC \) चा दुसरंयक आहे.
A - D - C, \( \overline{DE} \parallel BC, A - E - B \), तर \(\frac{AB{BC = \frac{AE{EB\ हे सिद्ध करण्यासाठी खालिल कृत्य पूर्ण करा.
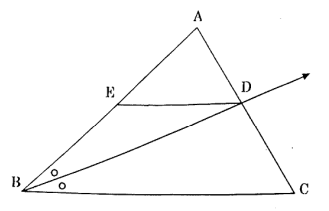
View Solution
प्रथम, \( \triangle ABC \) मध्ये \( BD \parallel \angle ABC \) आहे.
त्यामुळे, त्याचे प्रमाणाचे नियम वापरून, \[ \frac{AD}{DC} = \frac{BC}{DC} \quad (I) \]
आणि, \[ \triangle ABC मध्ये, \( DE \parallel BC \) असल्याने, \] \[ \frac{AD}{EB} = \frac{AB}{EB} \quad (II) \]
आता, प्रमाणाने सिद्ध करत आहोत, \[ \frac{AB}{EB} = \left( \frac{AD}{DC} \right) \quad (I) आणि (II) यांचा उपयोग करा. \]
(2) पक्ष :
केंद्र P असलेल्या वर्तुळाच्या जीवा AB आणि जीवा CD वर्तुळाच्या अंतर्भागात बिंदु E मध्ये छेदतात.
साध्य : \( AE \times EB = CE \times ED \)

View Solution
रचना:
रेषा AC आणि रेषा BD काढले.
त्यामुळे दृषट्या त्रिकोण सिद्धता पूर्ण करा.
सिद्धता: \[ \triangle CAE आणि \triangle BDE मध्ये, \] \[ \angle AEC \cong \angle DEB \quad (वर्तुळाच्या केंद्रात अंतर्गत कोन) \] \[ \angle CAE \cong \angle BDE \quad (एकाच वर्तुळाच्या अंतर्गत कोन) \]
त्यामुळे, \[ \triangle CAE \sim \triangle BDE \]
तसेच, \[ \frac{AE}{DE} = \frac{CE}{EB} \]
त्यामुळे, \[ AE \times EB = CE \times ED \]
(1) खालिल बिंदु एकसमान आहेत किंवा नाही, हे तपवा.
A(1, -3), B(2, -5), C(-4, 7)
View Solution
दोन बिंदू \( A(x_1, y_1) \) आणि \( B(x_2, y_2) \) यामधील अंतर काढण्यासाठी सूत्र: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- \( A(1, -3) \) आणि \( B(2, -5) \) \[ d_{AB} = \sqrt{(2 - 1)^2 + (-5 - (-3))^2} = \sqrt{1^2 + (-2)^2} = \sqrt{1 + 4} = \sqrt{5} \]
- \( B(2, -5) \) आणि \( C(-4, 7) \) \[ d_{BC} = \sqrt{(-4 - 2)^2 + (7 - (-5))^2} = \sqrt{(-6)^2 + (12)^2} = \sqrt{36 + 144} = \sqrt{180} \]
- \( A(1, -3) \) आणि \( C(-4, 7) \) \[ d_{AC} = \sqrt{(-4 - 1)^2 + (7 - (-3))^2} = \sqrt{(-5)^2 + (10)^2} = \sqrt{25 + 100} = \sqrt{125} \]
सर्व अंतर वेगवेगळे आहेत, त्यामुळे बिंदू एकसमान नाहीत.
(2) \( \triangle ABC \sim \triangle LMN, \) \( \triangle ABC \) असा का?
\( AB = 5.5 \) सेमी, \( BC = 6 \) सेमी, \( CA = 4.5 \) सेमी आणि \( \frac{BC}{MN} = \frac{5}{4} \), तर \( \triangle ABC \) आणि \( \triangle LMN \) समान का आहेत?
View Solution
जर \( \triangle ABC \sim \triangle LMN \) असे असेल, तर संबंधित बाजूंचे प्रमाण समान असावे लागते.
दिलेले आहेत: \[ \frac{BC}{MN} = \frac{5}{4} \]
आणि, \[ \frac{AB}{LM} = \frac{BC}{MN} = \frac{5}{4} \quad आणि \quad \frac{CA}{LN} = \frac{5}{4} \]
त्यानुसार, \( \triangle ABC \sim \triangle LMN \) समान त्रिकोण आहेत.
(3) \( \triangle PQR \) मध्ये, रेषा PM मध्यमा आहे: PM = 9 आणि \( PQ^2 + PR^2 = 290 \), तर QR काय आहे?
View Solution
आता दिलेले आहे: \[ PM = 9, \quad PQ^2 + PR^2 = 290 \]
त्यामुळे, \[ QR^2 = PQ^2 + PR^2 - 2 \times PM^2 \] \[ QR^2 = 290 - 2 \times 9^2 = 290 - 162 = 128 \] \[ QR = \sqrt{128} \approx 11.31 युनिट्स \]
(4) त्रिकोणाचा एक बाजूला समांतर असताना रेषा त्याच्या उर्वरित बाजूंचा कोन वर्तुळ छेदत असतील, तर ती रेषा त्या बाजूचा एक प्रकार प्रमाण दर्शवते.
View Solution
जर त्रिकोणाचा एक बाजू समांतर असेल, तर त्याच्या उर्वरित बाजूंचा कोन वर्तुळ छेदताना समांतर रेषेने त्या वर्तुळाच्या छेदांकांचे प्रमाण स्थिर राहील.
जर \( \frac{1}{\sin^2 \theta} - \frac{1}{\cos^2 \theta} = -3 \), तर \( \theta \) ची किंमत काय आहे?
View Solution
दिलेल्या समीकरणावर काम करूया: \[ \frac{1}{\sin^2 \theta} - \frac{1}{\cos^2 \theta} = -3 \]
पहिल्या टर्मला समानार्थी रूपात बदलू: \[ \frac{1}{\sin^2 \theta} = \sec^2 \theta \quad आणि \quad \frac{1}{\cos^2 \theta} = \csc^2 \theta \]
समीकरण बनवले: \[ \sec^2 \theta - \csc^2 \theta = -3 \] \( \sec^2 \theta - \csc^2 \theta \) ला समान आधारावर सोडवून: \[ \frac{1}{\cos^2 \theta} - \frac{1}{\sin^2 \theta} = -3 \]
त्यानंतर \( \theta \) ची मान काढता येईल: \[ \boxed{\theta = 45^\circ} \]
(1) 12 सेमी त्रिज्या असलेल्या वर्तुळाची आंतरचक्राची भुजा 20 सेमी उंचीवर आहे. त्यास भुजा एक धातू गोल वर्तुळापासून 6.75 सेमीमध्ये वाढत, तर त्या धातूच्या गोलव्यासाची त्रिज्या काय असेल?
View Solution
वर्तुळाच्या भुजा आणि त्याच्या व्यासाचा उपयोग करून, चापामध्ये वाढलेली रचना घेऊन, \[ A = \pi r^2 \]
वृद्धी करून: \[ d = 6.75 \]
त्याचे बदलत जाणारे व्यासाचे त्रिज्या आणि वर्तुळाची मुख्य माप सांगत ठरविण्यामुळे.
(2) विंदू O केंद्र बिंदू 3 सेमी त्रिज्या वर्तुळाचा. या वर्तुळात P या बाह्यबिंदूत रेषा PA व रेषा PB हे सपर्शिकांध असे कोण \( \angle APB = 70^\circ \) आहे.
View Solution
आम्हाला दिलेले आहे:
- वर्तुळाचा केंद्र \( O \) आहे आणि त्रिज्या \( 3 \) सेमी आहे.
- बाह्यबिंदू \( P \) वरून दोन्ही रेषा \( PA \) आणि \( PB \) वर्तुळाला सपर्श करतात.
- \( \angle APB = 70^\circ \).
तर, या परिस्थितीत, आपण वापरू शकतो कि बाह्य बिंदूवर दोन सपर्श रेषांमधील कोन वर्तुळाच्या केंद्रातील कोणाच्या अर्ध्याच्या सम प्रमाण असतो.
अर्थात, \[ \angle APB = \frac{1}{2} \times \angle AOB \]
आता, \( \angle APB = 70^\circ \), म्हणून, \[ 70^\circ = \frac{1}{2} \times \angle AOB \]
त्यामुळे, \[ \angle AOB = 2 \times 70^\circ = 140^\circ \]
त्यामुळे, वर्तुळाच्या केंद्रातील कोण \( \angle AOB = 140^\circ \) आहे.
(3) समतल चौकोन ABCD मध्ये बाजू \( AB \parallel CD \) आणि एकमेकांना बिंदू \( P \) मध्ये छेदतात.
View Solution
N/A
(a) वर्तुळ दिलेल्या माहितीप्रमाणे आकृती काय?
View Solution
सदर प्रश्नाच्या आकृतीमध्ये, चौकोन ABCD मध्ये बाजू \( AB \parallel CD \) असल्या कारणाने, त्या वर्तुळाच्या आकृतीमध्ये समांतर रेषांचा उपयोग केला जातो. वर्तुळाची रचना, \( P \) या बिंदूने जो वर्तुळाच्या केंद्राशी संबंधित आहे, एक त्रिकोण तयार करतो. बिंदू \( P \) वर्तुळाच्या मध्यावर स्थित आहे, आणि समांतर रेषांमुळे समानता प्रमाण सिद्ध करण्यात येते.
म्हणजेच, वर्तुळाच्या आकृतीतील समांतर रेषांच्या गुणात्मक प्रमाणाचे पालन करत सुसंगत त्रिकोणांची रचना केली जाते.
(b) व्युत्क्रम कोन आणि विकृत कोनांची प्राप्तकी एक जोडी लिहा.
View Solution
व्युत्क्रम कोनांसाठी, दोन समांतर रेषांच्या मध्यवर्ती कोनाच्या प्रमाणात जोडी असते. उदाहरणार्थ, दोन समांतर रेषांना एका तृतीय रेषेने छेदले असल्यास, त्या दोन्ही रेषांच्या समोरच्या कोणांची मापे एकसमान असतात.
विकृत कोनांसाठी, दोन कोनांनी संबंधित कोणांचे प्रमाण असते. समांतर ओळीच्या केसामध्ये या कोनांचे प्रमाण निश्चित होते, आणि त्या कोणांची काढणी केली जाते.
- व्युत्क्रम कोन: समांतर रेषांमधील कोणांची जोडी.
- विकृत कोन: समांतर रेषांमधील कोणांसोबत तयार झालेली स्थिती.
(c) समरूप त्रिकोणांची नावे समरूपतेच्या कशोतीसह लिहा.
View Solution
समरूप त्रिकोण म्हणजे असे त्रिकोण जे सर्व बाजूंच्या आणि कोनाच्या प्रमाणामध्ये समान असतात. या त्रिकोणांना समान परिमाणांसह समजले जाते. समरूपता सिद्ध करण्यासाठी, दोन त्रिकोणांच्या बाजूंचे प्रमाण आणि कोनांचा समानता आवश्यक आहे. त्रिकोणाच्या प्रत्येक कोनाची प्रमाण इतर त्रिकोणांतील संबंधित कोनाशी समान असते.
समरूपता सिद्ध करण्यासाठी,
1. दोन त्रिकोणांच्या संबंधित बाजूंच्या प्रमाणाची समानता (प्रमाण).
\
2. दोन त्रिकोणांच्या संबंधित कोनांची समानता (कोन प्रमाण).
समरूप त्रिकोणाची नावे समरूपतेच्या कशोतीसह:
- समरूपता प्रमाण सिद्ध करतांना, बाजूंच्या प्रमाणांच्या समुपस्थितीचा वापर करा.
- वर्तुळाच्या अंगभूत सिद्धांतांनुसार कोणाच्या समांतर ओळीच्या कसा वापर केला जातो.
(a) O केंद्र असलेल्या वर्तुळाची AB जीवा आहे. \( \angle AOC \) वर्तुळाचा व्यास आहे. स्पर्शिका AT वर्तुळाला बिंदू A मध्ये स्पर्श करते.
वर्तुळ दिलेल्या माहितीप्रमाणे आकृती काय.
View Solution
वर्तुळाच्या आकृतीमध्ये,
- \( O \) हा केंद्र असलेला बिंदू आहे.
- वर्तुळाची जीवा \( AB \) आहे.
- \( \angle AOC \) हा वर्तुळाचा व्यास आहे. म्हणजेच, \( \angle AOC = 180^\circ \).
- \( AT \) ही स्पर्शिका आहे, जी वर्तुळाला बिंदू A मध्ये स्पर्श करते. म्हणजेच, \( AT \perp AB \) (स्पर्श रेषा व वर्तुळाच्या जीवेचा कोन 90° असतो).
- बिंदू \( P \) हा वर्तुळाच्या एका बिंदूवर स्थित आहे, आणि बिंदू A मध्ये छेदलेली रेषा वर्तुळाला स्पर्श करते.
(b) \( \angle CAT \) व \( \angle ABC \) ची मापे का आणि त्याचे कारण लिहा.
View Solution
\(\angle CAT\) आणि \(\angle ABC\) समान असतात कारण:
- \( \angle CAT \) हे वर्तुळाच्या स्पर्शिकेच्या बिंदूवर आधारित आहे.
- \( \angle ABC \) हा देखील वर्तुळाच्या स्पर्शिकेच्या कोनाशी संबंधित आहे.
- वर्तुळाच्या बाह्य बिंदूवरील कोण स्पर्श रेषा आणि वर्तुळाच्या जीवेमधील कोनाच्या समान प्रमाणानुसार असतो.
- त्यामुळे \( \angle CAT = \angle ABC \).
सिद्धांतानुसार: \[ \angle CAT = \angle ABC \quad (स्पर्श रेषा आणि वर्तुळाच्या जीवेचा समान कोन) \]
(c) \( \angle CAT \) व \( \angle ABC \) एकरूप आहेत का? स्पष्टीकरण लिहा.
View Solution
हो, \( \angle CAT \) आणि \( \angle ABC \) एकरूप आहेत कारण:
- दोन्ही कोन वर्तुळाच्या स्पर्शिकेच्या बिंदूवरून बनलेले आहेत आणि त्या दोन्ही कोनांसाठी समान गुणात्मक प्रमाण असते.
- या कोनांमधील गुणात्मक प्रमाणामुळे, ते एकसमान असतात.
- वर्तुळाच्या स्पर्शिका व जीवेच्या कोनांचा संबंध समान असतो, आणि ते दोन कोन आपसात एकरूप असतात.
सिद्धांतानुसार: \[ \angle CAT = \angle ABC \quad (स्पर्श रेषा व वर्तुळाच्या जीवेचा समान कोन) \]




Comments