Maharashtra Board Class 10 Mathematics Algebra Part-1 Question Paper 2025 PDF (Code N 819) is available for download here. The Mathematics exam was conducted on March 5, 2025 from 11:00 AM to 2:00 PM. The Maharashtra State Board of Secondary and Higher Secondary Education (MSBSHSE) conducted the Class10 examination for a total duration of 3 hours, and the question paper had a total of 80 marks.
Maharashtra Board Class 10 Mathematics Algebra Part-1 Question Paper 2025 (Code N 819) with Solutions
| UP Board Class Mathematics Question Paper with Answer Key | Check Solutions |

Write the degree of the given determinant.
\begin{bmatrix} 1 & 2 \\[0.3em] 3 & 4 \\[0.3em] \end{bmatrix}
View Solution
Step 1: Understanding the Concept:
The degree (or order) of a determinant is defined by the number of rows or columns in the square matrix from which it is derived. A determinant of an \(n \times n\) matrix is said to have a degree of \(n\).
Step 2: Detailed Explanation:
The given determinant is:
\[ \begin{vmatrix} 1 & 2
3 & 4 \end{vmatrix} \]
We can observe that this matrix has:
- 2 rows (Row 1: [1 2], Row 2: [3 4])
- 2 columns (Column 1: \(\begin{bsmallmatrix} 1
3 \end{bsmallmatrix}\), Column 2: \(\begin{bsmallmatrix} 2
4 \end{bsmallmatrix}\))
Since the number of rows is 2 and the number of columns is 2, it is a \(2 \times 2\) determinant.
Step 3: Final Answer:
Therefore, the degree of the given determinant is 2.
Quick Tip: Do not confuse the degree of a determinant with its value. The value of this determinant would be \((1 \times 4) - (2 \times 3) = 4 - 6 = -2\), but its degree is simply the number of rows (or columns), which is 2.
From the following equations which one is the quadratic equation?
View Solution
Step 1: Understanding the Concept:
A quadratic equation is a polynomial equation of the second degree. The standard form of a quadratic equation in one variable \(x\) is \(ax^2 + bx + c = 0\), where \(a\), \(b\), and \(c\) are constants and \(a \neq 0\). The highest power of the variable must be 2.
Step 2: Detailed Explanation:
Let's analyze each option by simplifying it:
(A) \( \frac{5}{x} - 3 = x^2 \):
Multiplying the entire equation by \(x\) to eliminate the fraction gives:
\[ 5 - 3x = x^3 \] \[ x^3 + 3x - 5 = 0 \]
The highest power of \(x\) is 3, so this is a cubic equation, not a quadratic one.
(B) \( x(x + 5) = 2 \):
Expanding the left side:
\[ x^2 + 5x = 2 \]
Rearranging into standard form:
\[ x^2 + 5x - 2 = 0 \]
This equation is in the form \(ax^2 + bx + c = 0\) with \(a=1\), \(b=5\), and \(c=-2\). The highest power of \(x\) is 2. This is a quadratic equation.
(C) \( n - 1 = 2n \):
Rearranging the terms:
\[ 2n - n + 1 = 0 \] \[ n + 1 = 0 \]
The highest power of \(n\) is 1, so this is a linear equation.
(D) \( \frac{1}{x^2}(x + 2) = x \):
Multiplying the entire equation by \(x^2\) to eliminate the fraction gives:
\[ x + 2 = x^3 \] \[ x^3 - x - 2 = 0 \]
The highest power of \(x\) is 3, so this is a cubic equation.
Step 3: Final Answer:
Based on the analysis, only the equation \(x(x + 5) = 2\) simplifies to the standard form of a quadratic equation.
Quick Tip: To identify a quadratic equation, always simplify it first by removing fractions and expanding brackets. Then, check the highest power (degree) of the variable. If the degree is exactly 2, it's a quadratic equation.
Find the common difference of the following A.P. :
4, 4, 4, ...
View Solution
Step 1: Understanding the Concept:
An Arithmetic Progression (A.P.) is a sequence of numbers such that the difference between consecutive terms is constant. This constant difference is called the common difference, denoted by \(d\).
Step 2: Key Formula or Approach:
The formula to find the common difference is:
\[ d = a_{n+1} - a_n \]
Where \(a_{n+1}\) is the next term and \(a_n\) is the current term. We can calculate it using the first two terms: \(d = a_2 - a_1\).
Step 3: Detailed Explanation:
The given Arithmetic Progression is 4, 4, 4, ...
Here, the first term is \(a_1 = 4\).
The second term is \(a_2 = 4\).
The third term is \(a_3 = 4\).
Using the formula for the common difference:
\[ d = a_2 - a_1 = 4 - 4 = 0 \]
To verify, let's check the difference between the third and second terms:
\[ d = a_3 - a_2 = 4 - 4 = 0 \]
The difference is constant and equal to 0.
Step 4: Final Answer:
Therefore, the common difference of the given A.P. is 0.
Quick Tip: An A.P. where all the terms are the same is a constant sequence. For any constant sequence, the common difference is always 0.
Which number cannot represent a probability?
View Solution
Step 1: Understanding the Concept:
The probability of any event, P(E), is a number that must lie in the range from 0 to 1, inclusive. This is expressed mathematically as:
\[ 0 \leq P(E) \leq 1 \]
A probability of 0 means the event is impossible, and a probability of 1 means the event is certain. Any value outside this range cannot represent a probability.
Step 2: Detailed Explanation:
Let's evaluate each option to see if it falls within the [0, 1] range.
(A) \( \frac{2}{3} \):
As a decimal, \( \frac{2}{3} \approx 0.667 \). Since \( 0 \leq 0.667 \leq 1 \), this can represent a probability.
(B) \( \frac{15}{10} \):
As a decimal, \( \frac{15}{10} = 1.5 \). Since \( 1.5 > 1 \), this value is outside the valid range for probability. Therefore, it cannot represent a probability.
(C) 15%:
To convert a percentage to a decimal, divide by 100: \( 15% = \frac{15}{100} = 0.15 \). Since \( 0 \leq 0.15 \leq 1 \), this can represent a probability.
(D) 0.7:
This value is clearly between 0 and 1. Since \( 0 \leq 0.7 \leq 1 \), this can represent a probability.
Step 3: Final Answer:
The only number that falls outside the permissible range [0, 1] for a probability is \( \frac{15}{10} \).
Quick Tip: A simple way to check fractions is to see if the numerator is greater than the denominator. If the numerator is larger (an improper fraction), its value will be greater than 1, and thus it cannot be a probability.
Solve the following subquestions:
(i) If \( 2x + y = 7 \) and \( x + 2y = 11 \), then find the value of \( x + y \).
View Solution
We are given the following system of equations: \[ 2x + y = 7 \quad (Equation 1) \] \[ x + 2y = 11 \quad (Equation 2) \]
We need to solve for \( x + y \).
Let's use the method of substitution or elimination. We will first solve for \( y \) from Equation 1.
From Equation 1: \[ 2x + y = 7 \quad \Rightarrow \quad y = 7 - 2x \quad \cdots (3) \]
Now, substitute Equation (3) for \( y \) in Equation 2: \[ x + 2(7 - 2x) = 11 \]
Simplifying: \[ x + 14 - 4x = 11 \] \[ -3x + 14 = 11 \] \[ -3x = -3 \quad \Rightarrow \quad x = 1 \]
Now substitute \( x = 1 \) into Equation (3) to find \( y \): \[ y = 7 - 2(1) = 7 - 2 = 5 \]
Thus, \( x = 1 \) and \( y = 5 \), so: \[ x + y = 1 + 5 = 6 \]
Therefore, the value of \( x + y \) is 6. Quick Tip: When solving simultaneous equations, substitute one equation into the other to eliminate one variable and simplify the system.
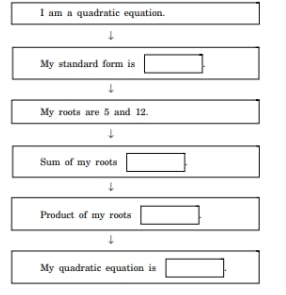
View Solution
N/A Quick Tip: To form a quadratic equation from the given roots, use the sum and product of the roots to write the equation as \( (x - r_1)(x - r_2) = 0 \), where \( r_1 \) and \( r_2 \) are the roots. Alternatively, use Vieta's formulas to directly derive the equation.
Pushpmala has invested ₹ 24,000 and purchased share of FV ₹ 20 at a premium of ₹ 4. Complete the following activity to find the number of shares she purchased.
Activity :
FV = ₹ 20
Premium = ₹ 4
MV = FV + \framebox[1.5cm]{\phantom{X}}
= 20 + \framebox[1.5cm]{\phantom{X}}
= ₹ 24
Number of shares = \(\frac{Total investment}{MV}\)
= \(\frac{24,000}{\framebox[1.5cm]{\phantom{X}}}\)
= \framebox[1.5cm]{\phantom{X}} shares.
View Solution
Step 1: Understanding the Concept:
This problem involves basic concepts of share market investments.
Face Value (FV): The nominal value of a share printed on the share certificate.
Premium: The amount paid for a share that is above its Face Value.
Market Value (MV): The price at which a share is actually bought or sold in the market.
Total Investment: The total amount of money used to purchase the shares.
Step 2: Key Formula or Approach:
The formulas needed to solve this activity are:
1. To calculate the Market Value (MV) of a share when it's at a premium:
\[ MV = Face Value (FV) + Premium \]
2. To calculate the number of shares purchased:
\[ Number of shares = \frac{Total Investment}{Market Value (MV) per share} \]
Step 3: Detailed Explanation:
We will complete the activity step-by-step using the given information and formulas.
Part 1: Calculate the Market Value (MV)
Given:
Face Value (FV) = ₹ 20
Premium = ₹ 4
Using the formula for MV:
\[ MV = FV + Premium \] \[ MV = 20 + 4 \] \[ MV = ₹ 24 \]
The first two blanks are 'Premium' and '4'.
Part 2: Calculate the Number of Shares
Given:
Total Investment = ₹ 24,000
Market Value (MV) = ₹ 24 (calculated above)
Using the formula for the number of shares:
\[ Number of shares = \frac{Total Investment}{MV} \] \[ Number of shares = \frac{24,000}{24} \] \[ Number of shares = 1000 \]
The next two blanks are '24' and '1000'.
Step 4: Final Answer:
The completed activity is as follows:
MV = FV + Premium
= 20 + 4
= ₹ 24
Number of shares = \(\frac{Total investment}{MV}\)
= \(\frac{24,000}{\textbf{24}}\)
= 1000 shares.
Pushpmala purchased 1000 shares.
Quick Tip: Always distinguish between Face Value (FV) and Market Value (MV). All calculations for the number of shares, investment, and returns are based on the Market Value, which is the actual transaction price. The dividend, however, is always calculated on the Face Value.
(i) Solve the simultaneous equations
\(x+y=3\) ; \(3x-2y=4\)
View Solution
Step 1: Write the system and isolate one variable from the simpler equation: \[ \begin{aligned} x+y&=3 \quad \tag{1}
3x-2y&=4 \quad \tag{2} \end{aligned} \qquad \Longrightarrow \qquad y=3-x (from (1)). \]
Step 2: Substitute \(y=3-x\) into (2) and solve for \(x\): \[ 3x-2(3-x)=4 \;\Rightarrow\; 3x-6+2x=4 \;\Rightarrow\; 5x=10 \;\Rightarrow\; x=2. \]
Step 3: Back-substitute into (1) to get \(y\): \[ 2+y=3 \;\Rightarrow\; y=1. \]
Check: In (2), \(3(2)-2(1)=6-2=4\), so the solution is correct. Quick Tip: For two linear equations, use \emph{substitution} when a variable has coefficient \(1\) or \(-1\), and \emph{elimination} when you can quickly cancel a variable by scaling and adding the equations. Always do a quick check in both equations.
(ii) Solve the quadratic equation \(m^2+14m+13=0\).
View Solution
Step 1: Factor by splitting the middle term. We want two numbers whose sum is \(14\) and product is \(13\): they are \(1\) and \(13\). \[ m^2+14m+13 = m^2+m+13m+13 = m(m+1)+13(m+1) = (m+1)(m+13). \]
Step 2: Set each factor to zero: \[ m+1=0 \;\Rightarrow\; m=-1, \qquad m+13=0 \;\Rightarrow\; m=-13. \]
Verification: Sum of roots \(= -1+(-13)=-14=-\frac{14}{1}\) and product \(= (-1)(-13)=13=\frac{13}{1}\), matching the coefficients. Quick Tip: For \(ax^2+bx+c=0\): if it factors neatly, use factoring; otherwise use the quadratic formula \(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\). A quick check: sum of roots \(=-\frac{b}{a}\) and product \(=\frac{c}{a}\).
(iii) Find the 19th term of the A.P. \(7,\,13,\,19,\,25,\ldots\)
View Solution
Step 1: Identify the first term and common difference: \[ a=7,\qquad d=13-7=6. \]
Step 2: Use the \(n\)-th term formula \(T_n=a+(n-1)d\): \[ T_{19}=7+(19-1)\cdot 6=7+18\cdot 6=7+108=115. \]
Sanity check: Terms grow by \(6\) each step; from \(T_1=7\) to \(T_{19}\) we add \(18\) steps of size \(6\), i.e., \(108\). Quick Tip: In any A.P., \(T_n=a+(n-1)d\) and \(S_n=\dfrac{n}{2}\big(2a+(n-1)d\big)\). Memorize both; they cover most A.P. questions quickly.
(iv) A share with market value \(₹2000\) is sold through a broker who charges \(0.5%\) brokerage. Find the amount received by the seller.
View Solution
Step 1: Compute brokerage as \(0.5%\) of the sale (market) value: \[ Brokerage=\frac{0.5}{100}\times 2000=0.005\times 2000=10. \]
Step 2: Net amount received \(=\) Sale value \(-\) Brokerage: \[ Amount received=2000-10=1990. \]
Interpretation: Brokerage is a fee deducted from the sale proceeds, so the seller receives the market value minus this fee. Quick Tip: For percentage deductions like brokerage, commission, or discount, use \(Net=Gross\times\left(1-\frac{r}{100}\right)\). Here, \(2000\times(1-0.5%)=2000\times 0.995=1990\).
The following table shows the number of students and the time they utilized daily for their studies. Find the mean time spent by the students for their studies.
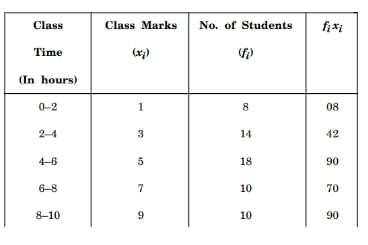
View Solution
Step 1: Compute \(\sum f_i\): \[ \sum f_i = 8+14+18+10+10 = 60. \]
Step 2: Compute \(\sum f_i x_i\): \[ \sum f_i x_i = 0\cdot 8 + 3\cdot 14 + 5\cdot 18 + 7\cdot 10 + 9\cdot 10 = 0+42+90+70+90=300. \]
Step 3: Apply the mean formula: \[ \bar{x}=\frac{\sum f_i x_i}{\sum f_i}=\frac{300}{60}=5. \] Quick Tip: When dealing with frequency distributions: \[ \bar{x}=\frac{\sum f_i x_i}{\sum f_i} \] Always check totals: \(\sum f_i\) (total frequency) and \(\sum f_i x_i\) (sum of products) before dividing.
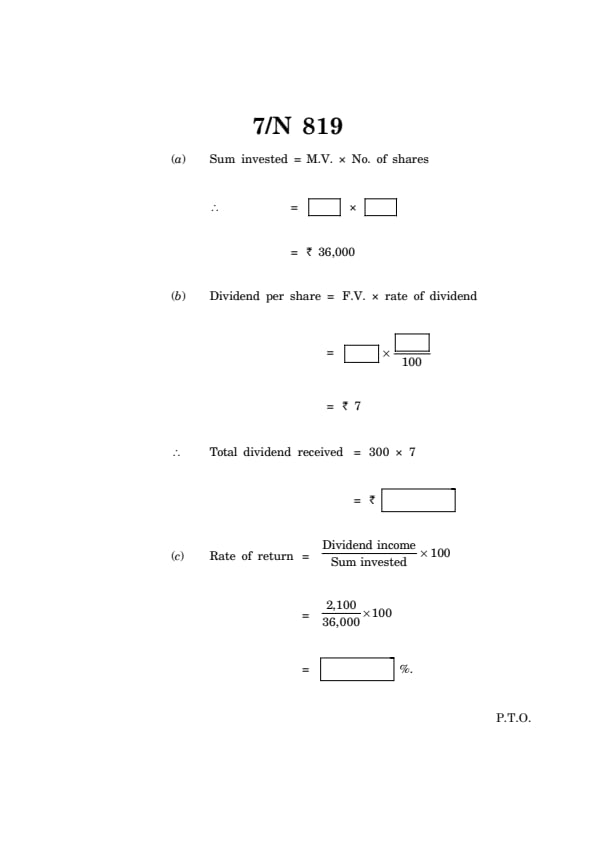
(i) Shri Maniklal has purchased 300 shares of F.V. ₹ 100, for M.V. ₹ 120. Company has paid dividend at 7%. Complete the following activity to find the rate of return on his investment.
Activity:
F.V. = ₹ 100
Number of shares = 300
Market value = ₹ 120
(a) Sum invested = M.V. \( \times \) No. of shares
\quad \(\therefore\) = \framebox[1.5cm]{\phantom{X \( \times \) \framebox[1.5cm]{\phantom{X
\quad \qquad \qquad = ₹ 36,000
(b) Dividend per share = F.V. \( \times \) rate of dividend
= \framebox[1.5cm]{\phantom{X \( \times \) \(\frac{\framebox{\phantom{X}}}{100}\)
= ₹ 7
\(\therefore\) Total dividend received = 300 \( \times \) 7
= ₹ \framebox[1.5cm]{\phantom{X
(c) Rate of return = \(\frac{Dividend income}{Sum invested} \times 100\)
= \(\frac{2,100}{36,000} \times 100\)
= \framebox{\phantom{X %.
View Solution
Step 1: Understanding the Concept:
This activity requires calculating the rate of return on an investment in shares. The rate of return is the percentage of the total dividend income relative to the total amount invested (based on Market Value).
Step 2: Key Formula or Approach:
1. Sum Invested = Market Value (M.V.) \( \times \) Number of shares.
2. Dividend Income = (Face Value (F.V.) \( \times \) Dividend Rate) \( \times \) Number of shares.
3. Rate of Return = \( \left( \frac{Total Dividend Income}{Sum Invested} \right) \times 100 \).
Step 3: Detailed Explanation:
Here is the completed activity with the blanks filled in.
F.V. = ₹ 100
Number of shares = 300
Market value = ₹ 120
(a) Sum invested = M.V. \( \times \) No. of shares
\quad \(\therefore\) \qquad \qquad = \framebox[1.5cm]{120 \( \times \) \framebox[1.5cm]{300
\quad \qquad \qquad = ₹ 36,000
(b) Dividend per share = F.V. \( \times \) rate of dividend
\quad \qquad \qquad = \framebox[1.5cm]{100 \( \times \) \(\frac{\framebox[1.5cm]{\textbf{7}}}{100}\)
\quad \qquad \qquad = ₹ 7
\quad \(\therefore\) Total dividend received = 300 \( \times \) 7
\quad \qquad \qquad = ₹ \framebox[1.5cm]{2,100
(c) Rate of return = \(\frac{Dividend income}{Sum invested} \times 100\)
\quad \qquad \qquad = \(\frac{2,100}{36,000} \times 100\)
\quad \qquad \qquad = \(\frac{2,100}{360}\)
\quad \qquad \qquad = \(\frac{210}{36} = \frac{35}{6} \approx 5.83\)
\quad \qquad \qquad = \framebox[1.5cm]{5.83 %.
Step 4: Final Answer:
The rate of return on the investment is 5.83%.
Quick Tip: Always remember that the dividend is calculated on the Face Value (F.V.) of a share, but the investment amount and the rate of return are calculated based on the Market Value (M.V.).
A two digit number is to be formed from the digits 2, 3, 5 without repetition of the digits. Complete the following activity to find the probability that the number so formed is an odd number.
Activity:
Let S be the sample space.
\(\therefore\) S = \{23, 25, 32, \framebox[1.5cm]{\phantom{X, 52, 53\
\(\therefore\) n(S) = \framebox[1.5cm]{\phantom{X
Event A: The number so formed is an odd number.
\(\therefore\) A = \{23, 25, \framebox[1.5cm]{\phantom{X, 53\
\(\therefore\) n(A) = 4
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\phantom{X}}}{n(S)}\) \dots \dots (Formula)
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\phantom{X}}}{6}\)
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\phantom{X}}}{3}\)
View Solution
Step 1: Understanding the Concept:
This activity involves finding the probability of an event. We first need to list all possible outcomes (the sample space) when forming two-digit numbers from the digits 2, 3, 5 without repetition. Then, we identify the favorable outcomes (the odd numbers) and use the probability formula.
Step 2: Key Formula or Approach:
Probability of an event A, P(A) = \( \frac{Number of favorable outcomes}{Total number of outcomes} = \frac{n(A)}{n(S)} \).
Step 3: Detailed Explanation:
Here is the completed activity with the blanks filled in.
Let S be the sample space. The two-digit numbers formed from 2, 3, 5 without repetition are:
Using 2 in tens place: 23, 25
Using 3 in tens place: 32, 35
Using 5 in tens place: 52, 53
\(\therefore\) S = \{23, 25, 32, \framebox[1.5cm]{35, 52, 53\
\(\therefore\) n(S) = \framebox[1.5cm]{6
Event A: The number so formed is an odd number. An odd number has an odd digit (3 or 5) in the unit's place.
The odd numbers from the sample space are 23, 25, 35, 53.
\(\therefore\) A = \{23, 25, \framebox[1.5cm]{35, 53\
\(\therefore\) n(A) = 4
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\textbf{n(A)}}}{n(S)}\) \dots \dots (Formula)
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\textbf{4}}}{6}\)
\(\therefore\) P(A) = \(\frac{\framebox[1.5cm]{\textbf{2}}}{3}\)
Step 4: Final Answer:
The probability that the number formed is an odd number is \( \frac{2}{3} \).
Quick Tip: For probability questions, always start by systematically listing all possible outcomes in the sample space (S). This prevents errors in counting n(S). Then, carefully list the outcomes that satisfy the event's condition to find n(A).
(i) Solve the following simultaneous equations by Cramer's rule:
4x + 3y = 18; 3x - 2y = 5
View Solution
Step 1: Understanding the Concept:
Cramer's rule is a method for solving a system of linear equations using determinants. For a system of two equations:
\( a_1x + b_1y = c_1 \)
\( a_2x + b_2y = c_2 \)
The solution is given by \( x = \frac{D_x}{D} \) and \( y = \frac{D_y}{D} \).
Step 2: Key Formula or Approach:
The determinants are calculated as follows: \[ D = \begin{vmatrix} a_1 & b_1
a_2 & b_2 \end{vmatrix} = a_1b_2 - a_2b_1 \] \[ D_x = \begin{vmatrix} c_1 & b_1
c_2 & b_2 \end{vmatrix} = c_1b_2 - c_2b_1 \] \[ D_y = \begin{vmatrix} a_1 & c_1
a_2 & c_2 \end{vmatrix} = a_1c_2 - a_2c_1 \]
Step 3: Detailed Explanation:
The given equations are:
\( 4x + 3y = 18 \) \dots(1)
\( 3x - 2y = 5 \) \dots(2)
Here, \( a_1 = 4, b_1 = 3, c_1 = 18 \) and \( a_2 = 3, b_2 = -2, c_2 = 5 \).
First, we calculate the determinant D: \[ D = \begin{vmatrix} 4 & 3
3 & -2 \end{vmatrix} = (4 \times -2) - (3 \times 3) = -8 - 9 = -17 \]
Next, we calculate the determinant \( D_x \): \[ D_x = \begin{vmatrix} 18 & 3
5 & -2 \end{vmatrix} = (18 \times -2) - (5 \times 3) = -36 - 15 = -51 \]
Now, we calculate the determinant \( D_y \): \[ D_y = \begin{vmatrix} 4 & 18
3 & 5 \end{vmatrix} = (4 \times 5) - (3 \times 18) = 20 - 54 = -34 \]
Using Cramer's rule: \[ x = \frac{D_x}{D} = \frac{-51}{-17} = 3 \] \[ y = \frac{D_y}{D} = \frac{-34}{-17} = 2 \]
Step 4: Final Answer:
The solution to the simultaneous equations is \( x = 3 \) and \( y = 2 \).
Quick Tip: Be very careful with signs when calculating determinants, especially when coefficients are negative. A small sign error will lead to an incorrect final answer. It's a good practice to double-check your determinant calculations.
Solve the following quadratic equation by using formula method:
x\(^2\) - 2x - 3 = 0
View Solution
Step 1: Understanding the Concept:
The formula method is used to find the roots of a quadratic equation of the form \( ax^2 + bx + c = 0 \).
Step 2: Key Formula or Approach:
The quadratic formula is: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
The term \( b^2 - 4ac \) is called the discriminant (\(\Delta\)).
Step 3: Detailed Explanation:
The given quadratic equation is \( x^2 - 2x - 3 = 0 \).
Comparing this with the standard form \( ax^2 + bx + c = 0 \), we get: \[ a = 1, \quad b = -2, \quad c = -3 \]
First, we calculate the discriminant, \( \Delta = b^2 - 4ac \): \[ \Delta = (-2)^2 - 4(1)(-3) \] \[ \Delta = 4 - (-12) \] \[ \Delta = 4 + 12 = 16 \]
Now, we substitute the values of a, b, and \(\Delta\) into the quadratic formula: \[ x = \frac{-(-2) \pm \sqrt{16}}{2(1)} \] \[ x = \frac{2 \pm 4}{2} \]
The two roots are: \[ x_1 = \frac{2 + 4}{2} = \frac{6}{2} = 3 \] \[ x_2 = \frac{2 - 4}{2} = \frac{-2}{2} = -1 \]
Step 4: Final Answer:
The roots of the quadratic equation are 3 and -1.
Quick Tip: Always calculate the discriminant (\(b^2 - 4ac\)) separately first. This simplifies the main formula and helps avoid calculation errors. If the discriminant is a perfect square, you know the roots will be rational.
A committee of two members is to be formed from three boys and two girls. Find the probability of the following events:
Event A: At least one girl must be a member of the committee.
Event B: Committee must be of one boy and one girl.
View Solution
Step 1: Understanding the Concept:
This problem involves calculating probabilities of events based on combinations. First, we need to find the total number of ways to form the committee (sample space), and then find the number of ways for each specific event.
Let the three boys be B\(_1\), B\(_2\), B\(_3\) and the two girls be G\(_1\), G\(_2\). Total persons = 5.
Step 2: Key Formula or Approach:
1. The number of combinations of choosing \(r\) items from a set of \(n\) is given by \( {}^nC_r = \frac{n!}{r!(n-r)!} \).
2. Probability of an event = \( \frac{Number of favorable outcomes}{Total number of outcomes} \).
Step 3: Detailed Explanation:
Sample Space (S):
We need to form a committee of 2 members from a total of 5 people (3 boys + 2 girls). \[ n(S) = {}^5C_2 = \frac{5!}{2!(5-2)!} = \frac{5 \times 4}{2 \times 1} = 10 \]
So, there are 10 possible committees.
Event A: At least one girl must be a member.
"At least one girl" means the committee can have (one girl and one boy) OR (two girls).
Case 1: One girl and one boy
Number of ways = (Choose 1 girl from 2) \( \times \) (Choose 1 boy from 3) \[ = {}^2C_1 \times {}^3C_1 = 2 \times 3 = 6 \]
Case 2: Two girls
Number of ways = (Choose 2 girls from 2) \[ = {}^2C_2 = 1 \]
Total number of ways for Event A, n(A) = 6 + 1 = 7.
Probability of Event A: \[ P(A) = \frac{n(A)}{n(S)} = \frac{7}{10} \]
Alternatively, for Event A:
The complement of "at least one girl" is "no girls" (i.e., both are boys).
Number of ways to choose 2 boys from 3 = \( {^3C_2 = 3 \).
P(no girl) = \( \frac{3}{10} \).
P(at least one girl) = 1 - P(no girl) = \( 1 - \frac{3}{10} = \frac{7}{10} \).
Event B: Committee must be of one boy and one girl.
This is the same as Case 1 calculated for Event A.
Number of ways for Event B, n(B) = (Choose 1 boy from 3) \( \times \) (Choose 1 girl from 2) \[ n(B) = {}^3C_1 \times {}^2C_1 = 3 \times 2 = 6 \]
Probability of Event B: \[ P(B) = \frac{n(B)}{n(S)} = \frac{6}{10} = \frac{3}{5} \]
Step 4: Final Answer:
The probability of Event A (at least one girl) is \( \frac{7}{10} \).
The probability of Event B (one boy and one girl) is \( \frac{6}{10} \) or \( \frac{3}{5} \).
Quick Tip: For "at least one" probability questions, it is often much easier to calculate the probability of the complementary event ("none") and subtract it from 1.
In a general store the prices of different articles and its demand is shown in the following frequency distribution table. Find the Median of the prices.

View Solution
Step 1: Understanding the Concept:
The median is the middle value in a dataset. For grouped data, we find the median class and then use a formula to estimate the median value. The given table has a 'less than' type entry for the first row, which we interpret as the first class interval (0-20).
Step 2: Key Formula or Approach:
The formula for the median of grouped data is: \[ Median = L + \left[ \frac{\frac{N}{2} - cf}{f} \right] \times h \]
where:
L = Lower class boundary of the median class.
N = Total frequency (\(\Sigma f\)).
cf = Cumulative frequency of the class preceding the median class.
f = Frequency of the median class.
h = Class width of the median class.
Step 3: Detailed Explanation:
First, we construct the frequency distribution table with class intervals, frequencies (f), and cumulative frequencies (cf). The class "Less than 20" is taken as 0-20.
\begin{tabular{|c|c|c|
\hline
Class Interval & Frequency (f) & Cumulative Frequency (cf)
\hline
0--20 & 140 & 140
20--40 & 100 & 140 + 100 = 240
40--60 & 80 & 240 + 80 = 320
60--80 & 60 & 320 + 60 = 380
80--100 & 20 & 380 + 20 = 400
\hline
Total & N = 400 &
\hline
\end{tabular
1. Find N/2: \[ N = \Sigma f = 400 \] \[ \frac{N}{2} = \frac{400}{2} = 200 \]
2. Identify the Median Class:
The cumulative frequency just greater than 200 is 240. The corresponding class is 20--40. This is the median class.
3. Identify the values for the formula:
L (Lower limit of median class) = 20
cf (Cumulative frequency of the preceding class) = 140
f (Frequency of the median class) = 100
h (Class width) = 40 - 20 = 20
4. Calculate the Median: \[ Median = L + \left[ \frac{\frac{N}{2} - cf}{f} \right] \times h \] \[ Median = 20 + \left[ \frac{200 - 140}{100} \right] \times 20 \] \[ Median = 20 + \left[ \frac{60}{100} \right] \times 20 \] \[ Median = 20 + (0.6) \times 20 \] \[ Median = 20 + 12 \] \[ Median = 32 \]
Step 4: Final Answer:
The Median of the prices is ₹ 32.
Quick Tip: When a frequency table contains a mix of 'less than' and class intervals, carefully construct a standard class interval table first. The key is to correctly create the cumulative frequency (cf) column, as all values in the median formula depend on it.
(i) Find the value of 'm' if the quadratic equation
(m - 12) x\(^2\) + 2(m - 12)x + 2 = 0
has real and equal roots.
View Solution
Step 1: Understanding the Concept:
For a quadratic equation of the form \(ax^2 + bx + c = 0\), the roots are real and equal if its discriminant (\(\Delta\)) is equal to zero.
Step 2: Key Formula or Approach:
The discriminant is given by the formula: \[ \Delta = b^2 - 4ac \]
For real and equal roots, we must have: \[ b^2 - 4ac = 0 \]
Step 3: Detailed Explanation:
The given quadratic equation is \( (m - 12) x^2 + 2(m - 12)x + 2 = 0 \).
Comparing this with the standard form \(ax^2 + bx + c = 0\), we get: \[ a = m - 12 \] \[ b = 2(m - 12) \] \[ c = 2 \]
For the equation to be quadratic, \(a \neq 0\), which means \(m - 12 \neq 0\), so \(m \neq 12\).
Now, we set the discriminant to zero: \[ \Delta = [2(m - 12)]^2 - 4(m - 12)(2) = 0 \] \[ 4(m - 12)^2 - 8(m - 12) = 0 \]
We can factor out \(4(m - 12)\) from the expression: \[ 4(m - 12) [(m - 12) - 2] = 0 \] \[ 4(m - 12)(m - 14) = 0 \]
This gives two possible solutions: \(m - 12 = 0\) or \(m - 14 = 0\).
So, \(m = 12\) or \(m = 14\).
However, as we established earlier, for the equation to be quadratic, \(m \neq 12\).
Therefore, we must discard the solution \(m = 12\).
The only valid solution is \(m = 14\).
Step 4: Final Answer:
The value of 'm' for which the quadratic equation has real and equal roots is 14.
Quick Tip: When solving for a variable in the coefficient of the \(x^2\) term, always check if your solution makes that coefficient zero. If it does, that value must be rejected because the equation would no longer be quadratic.
A farmer borrows ₹ 1,000 and agrees to repay with a total interest of ₹ 140, in 12 instalments. Each instalment being less than the preceding instalment by ₹ 10. What should be the amount of his first and last instalment?
View Solution
Step 1: Understanding the Concept:
The instalments form an Arithmetic Progression (A.P.) because the difference between consecutive instalments is constant. We are given the total amount to be repaid (sum of the A.P.), the number of terms, and the common difference. We need to find the first and last terms.
Step 2: Key Formula or Approach:
1. Sum of n terms of an A.P.: \( S_n = \frac{n}{2} [2a + (n-1)d] \)
2. The n-th term of an A.P.: \( t_n = a + (n-1)d \)
where \(a\) is the first term, \(n\) is the number of terms, and \(d\) is the common difference.
Step 3: Detailed Explanation:
Total amount to be repaid = Principal + Interest \[ S_n = 1000 + 140 = ₹ 1140 \]
Number of instalments, \(n = 12\).
Each instalment is ₹ 10 less than the preceding one, so the common difference, \(d = -10\).
Let the first instalment be \(a\).
Using the sum formula to find \(a\): \[ S_{12} = \frac{12}{2} [2a + (12-1)(-10)] \] \[ 1140 = 6 [2a + (11)(-10)] \] \[ 1140 = 6 [2a - 110] \]
Divide both sides by 6: \[ \frac{1140}{6} = 2a - 110 \] \[ 190 = 2a - 110 \] \[ 190 + 110 = 2a \] \[ 300 = 2a \] \[ a = 150 \]
So, the first instalment is ₹ 150.
Now, we find the last instalment, which is the 12th term (\(t_{12}\)).
Using the n-th term formula: \[ t_{12} = a + (12-1)d \] \[ t_{12} = 150 + (11)(-10) \] \[ t_{12} = 150 - 110 \] \[ t_{12} = 40 \]
So, the last instalment is ₹ 40.
Step 4: Final Answer:
The amount of the first instalment is ₹ 150 and the amount of the last instalment is ₹ 40.
Quick Tip: Pay close attention to the wording. "Less than the preceding" implies a negative common difference. Also, remember that the total amount repaid (\(S_n\)) is the sum of the principal and the interest.
The following table shows the marks of 180 students in Mathematics.
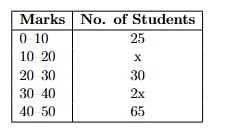
Find the value of 'x' and draw histogram.
View Solution
Step 1: Understanding the Concept:
The total number of students is the sum of the frequencies of all class intervals. We can set up an equation to find the value of 'x'. A histogram is a graphical representation of this frequency distribution where class intervals are on the x-axis and frequencies are on the y-axis.
Step 2: Key Formula or Approach:
Total Frequency (\(N\)) = Sum of all individual frequencies (\(\Sigma f_i\)).
Step 3: Detailed Explanation:
Part 1: Finding the value of 'x'
The total number of students is given as 180. \[ N = \Sigma f_i = 180 \]
Summing the frequencies from the table: \[ 25 + x + 30 + 2x + 65 = 180 \]
Combine the constant terms and the 'x' terms: \[ (25 + 30 + 65) + (x + 2x) = 180 \] \[ 120 + 3x = 180 \] \[ 3x = 180 - 120 \] \[ 3x = 60 \] \[ x = \frac{60}{3} = 20 \]
Now we can find the frequencies for the classes 10-20 and 30-40:
Frequency for 10--20 = \(x\) = 20
Frequency for 30--40 = \(2x\) = 2(20) = 40
The complete frequency table is:
\begin{tabular{|l|c|
\hline
Marks & No. of Students
\hline
0--10 & 25
10--20 & 20
20--30 & 30
30--40 & 40
40--50 & 65
\hline
Total & 180
\hline
\end{tabular
Part 2: Drawing the Histogram
To draw the histogram:
Draw the X-axis and Y-axis on graph paper.
On the X-axis, represent the Marks (class intervals). Choose an appropriate scale, for example, 1 cm = 10 marks. The intervals are continuous (0-10, 10-20, etc.).
On the Y-axis, represent the Number of Students (frequency). Choose an appropriate scale, for example, 1 cm = 10 students.
For each class interval, draw a rectangle (bar) with the width equal to the class interval and height equal to the corresponding frequency. The bars should be adjacent to each other without any gaps.
For 0--10, the bar height is 25.
For 10--20, the bar height is 20.
For 20--30, the bar height is 30.
For 30--40, the bar height is 40.
For 40--50, the bar height is 65.
Label the axes and provide a title for the histogram, e.g., "Marks Distribution of 180 Students".
Step 4: Final Answer:
The value of x is 20. The histogram should be drawn on graph paper as described above using the calculated frequencies.
Quick Tip: For histograms, ensure that the class intervals are continuous. If they are not, you must adjust the boundaries first. In this case, the classes are already continuous, so you can draw the adjacent bars directly. Always choose a clear and consistent scale for both axes.
(i) Draw the graphs representing the equation 2x = y + 2 and 4x + 3y = 24 on the same graph paper. Find the area of the triangle formed by these lines and the X-axis.
View Solution
Step 1: Understanding the Concept:
We need to plot two linear equations on a graph. The two lines and the X-axis will form a triangle. The vertices of this triangle will be the x-intercept of the first line, the x-intercept of the second line, and the point of intersection of the two lines. We can then find the area of this triangle.
Step 2: Key Formula or Approach:
Area of a triangle = \( \frac{1}{2} \times base \times height \).
Step 3: Detailed Explanation:
Part 1: Plotting the graphs
First, we find at least two points for each equation to draw the lines.
Line 1: 2x = y + 2 \(\implies\) y = 2x - 2
\begin{tabular{|c|c|c|c|
\hline
x & 0 & 1 & 2
\hline
y & -2 & 0 & 2
\hline
\end{tabular
Points are (0, -2), (1, 0), (2, 2). The x-intercept is (1, 0).
Line 2: 4x + 3y = 24
\begin{tabular{|c|c|c|c|
\hline
x & 0 & 6 & 3
\hline
y & 8 & 0 & 4
\hline
\end{tabular
Points are (0, 8), (6, 0), (3, 4). The x-intercept is (6, 0).
The graphs should be plotted on graph paper using these points.
Part 2: Finding the vertices of the triangle
The vertices of the triangle are:
Vertex A: The x-intercept of Line 1, which is (1, 0).
Vertex B: The x-intercept of Line 2, which is (6, 0).
Vertex C: The intersection point of the two lines.
To find Vertex C, we solve the two equations simultaneously:
\( y = 2x - 2 \)
\( 4x + 3y = 24 \)
Substitute (1) into (2): \[ 4x + 3(2x - 2) = 24 \] \[ 4x + 6x - 6 = 24 \] \[ 10x = 30 \] \[ x = 3 \]
Now find y by substituting x=3 into equation (1): \[ y = 2(3) - 2 = 6 - 2 = 4 \]
So, Vertex C is (3, 4).
Part 3: Finding the area of the triangle
The triangle has vertices A(1, 0), B(6, 0), and C(3, 4).
The base of the triangle is the segment AB on the X-axis. \[ Base = distance between (1, 0) and (6, 0) = 6 - 1 = 5 units. \]
The height of the triangle is the perpendicular distance from vertex C to the base on the X-axis. This is the y-coordinate of point C. \[ Height = 4 units. \]
Now, we calculate the area: \[ Area = \frac{1}{2} \times base \times height \] \[ Area = \frac{1}{2} \times 5 \times 4 = 10 sq. units. \]
Step 4: Final Answer:
The area of the triangle formed by the lines and the X-axis is 10 square units.
Quick Tip: To easily find the vertices of a triangle formed by two lines and an axis, find the intercepts of the lines with that axis and the intersection point of the two lines. The base will be the distance between the intercepts, and the height will be the perpendicular coordinate of the intersection point.
The following pie-diagram shows percentage of persons according to blood group in a blood group checking camp. Answer the following questions:
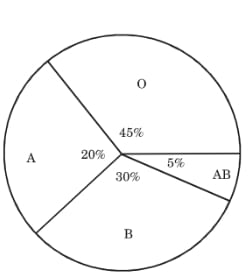
(a) Find the measure of central angle for each blood group.
(b) Find the total number of persons, if there are 600 persons of blood group B.
View Solution
Step 1: Understanding the Concept:
A pie chart represents a whole dataset, where the total is equivalent to 100% or 360\(^\circ\). The central angle for each sector is proportional to the percentage it represents.
Step 2: Key Formula or Approach:
(a) Central Angle = \( \frac{Percentage of component}{100} \times 360^\circ \)
(b) Total number = \( \frac{Given number for a component}{Percentage of that component} \times 100 \)
Step 3: Detailed Explanation:
(a) Find the measure of central angle for each blood group.
Blood Group O (45%):
Central Angle = \( \frac{45}{100} \times 360^\circ = 0.45 \times 360^\circ = 162^\circ \)
Blood Group A (20%):
Central Angle = \( \frac{20}{100} \times 360^\circ = 0.20 \times 360^\circ = 72^\circ \)
Blood Group B (30%):
Central Angle = \( \frac{30}{100} \times 360^\circ = 0.30 \times 360^\circ = 108^\circ \)
Blood Group AB (5%):
Central Angle = \( \frac{5}{100} \times 360^\circ = 0.05 \times 360^\circ = 18^\circ \)
(Check: 162 + 72 + 108 + 18 = 360\(^\circ\))
(b) Find the total number of persons, if there are 600 persons of blood group B.
From the pie chart, the percentage of persons with blood group B is 30%.
Let the total number of persons be 'T'.
We are given that 30% of T is 600.
\[ \frac{30}{100} \times T = 600 \]
To find T, we rearrange the formula: \[ T = \frac{600 \times 100}{30} \] \[ T = 20 \times 100 \] \[ T = 2000 \]
So, the total number of persons in the camp was 2000.
Step 4: Final Answer:
(a) The central angles are: O = 162\(^\circ\), A = 72\(^\circ\), B = 108\(^\circ\), AB = 18\(^\circ\).
(b) The total number of persons is 2000.
Quick Tip: When converting percentages to degrees for a pie chart, you can remember that 1% is equal to 3.6\(^\circ\) (\(360/100\)). You can then simply multiply each percentage by 3.6 to find the central angle.













Comments