Maharashtra Board Class 10 MATHEMATICS-ALGEBRA-71-N-927 Question Paper 2023 with Solution PDF

If \(a\), \(b\), \(c\) are sides of a triangle and \(a^2 + b^2 = c^2\), name the type of triangle:

• (A) Obtuse angled triangle
• (B) Acute angled triangle
• (C) Right angled triangle
• (D) Equilateral triangle

Chords AB and CD of a circle intersect inside the circle at point E. If AE = 4, EB = 10, and CE = 8, then find ED:

• (A) 7
• (B) 5
• (C) 8
• (D) 9

Co-ordinates of origin are:

• (A) (0, 0)
• (B) (0, 1)
• (C) (1, 0)
• (D) (1, 1)

If the radius of the base of a cone is 7 cm and the height is 24 cm, find its slant height:

• (A) 23 cm
• (B) 26 cm
• (C) 31 cm
• (D) 25 cm

If \(\triangle ABC \sim \triangle PQR\) and \(\dfrac{A(\triangle ABC)}{A(\triangle PQR)} = \dfrac{16}{25}\), then find \(AB : PQ\).

In \(\triangle RST\), \(\angle S = 90^\circ\), \(\angle T = 30^\circ\), and \(RT = 12\) cm, then find \(RS\).

If the radius of a circle is 5 cm, then find the length of the longest chord of the circle.

Find the distance between the points \(O(0, 0)\) and \(P(3, 4)\).

In the figure below, \(\angle L = 35^\circ\). Find:

• (i) \(m(arc MN)\)
• (ii) \(m(arc MLN)\)

Show that, \(\cot \theta + \tan \theta = \csc \theta \times \sec \theta\)

Find the surface area of a sphere of radius 7 cm.

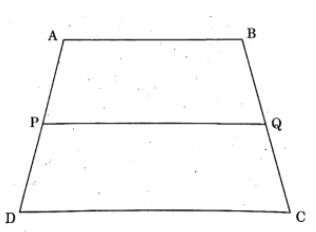
In trapezium \(ABCD\), side \(AB \parallel PQ \parallel DC\). If \(AP = 3\), \(PD = 12\), and \(QC = 14\), find \(BQ\).
 

Find the length of the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.

In the given figure, points G, D, E, F are points on a circle with centre C. If \(\angle ECF = 70^\circ\) and \(m(arc DGF) = 200^\circ\), find:

• (i) \(m(arc DE)\)
• (ii) \(m(arc DEF)\)

Show that points A(\(-1, -1\)), B(\(0, 1\)), and C(\(1, 3\)) are collinear.

A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is \(45^\circ\). Find the height of the temple.

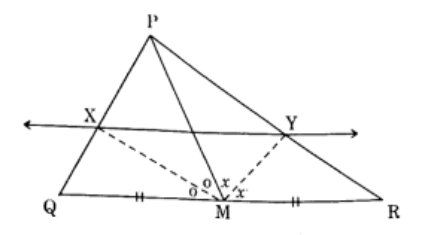
In \(\triangle PQR\), seg \(PM\) is a median. Angle bisectors of \(\angle PMQ\) and \(\angle PMR\) intersect sides \(PQ\) and \(PR\) in points \(X\) and \(Y\) respectively. Prove that \(XY \parallel QR\).
 

Find the co-ordinates of point P where P is the midpoint of a line segment AB with A(\(-4\), 2) and B(6, 2).
 

In \(\triangle ABC\), seg \(AP\) is a median. If \(BC = 18\), and \(AB^2 + AC^2 = 260\), find \(AP\).

Prove that, “Angles inscribed in the same arc are congruent.”

Draw a circle of radius 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q.

The radii of the circular ends of a frustum are 14 cm and 6 cm respectively, and its height is 6 cm. Find its curved surface area. (\(\pi = 3.14\))

In \(\triangle ABC\), seg \(DE \parallel BC\). If \(2A(\triangle ADE) = A(\triangle DBCE)\), find \(AB : AD\) and show that \(BC = \sqrt{3} \, DE\).

\(\triangle SHR \sim \triangle SVU\). In \(\triangle SHR\), \(SH = 4.5\) cm, \(HR = 5.2\) cm, and \(SR = 5.8\) cm. If \(\dfrac{SH}{SV} = \dfrac{3}{5}\), construct \(\triangle SVU\).

An ice-cream pot has a right circular cylindrical shape. The radius of the base is 12 cm and the height is 7 cm. This pot is completely filled with ice-cream. The entire ice-cream is given to students in the form of right circular cones having diameter 4 cm and height 3.5 cm. If each student is given one cone, how many students can be served?

A circle touches side \(BC\) at point \(P\) of \(\triangle ABC\), from outside of the triangle. Further extended lines \(AC\) and \(AB\) are tangents to the circle at \(N\) and \(M\) respectively. Prove that:
 

Eliminate \(\theta\) if \(x = r \cos \theta\) and \(y = r \sin \theta\).