
Muskan Shafi Education Content Expert
Education Content Expert
Value of Cos 180 Degrees is -1. Cos or Cosine is one of the most commonly used trigonometric ratios in Mathematics.
- Trigonometry is a branch of Mathematics that deals with the length, height, and angles of a right-angled triangle.
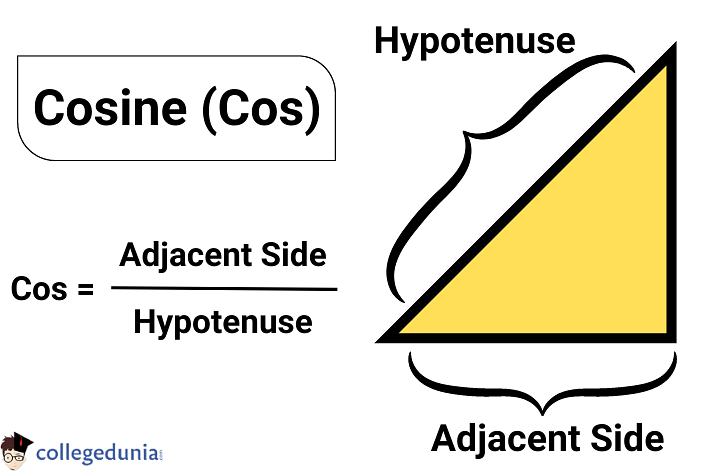
- Cosine Function (cos Function) is the ratio of the adjacent side to that of the hypotenuse in a triangle.
- It is denoted as cos x, where x is the angle.
- Cos 180 Degrees is equal to -1.
- Cos 180 Degrees is written as cos (180° × π/180°) in radians, i.e. cos (π) or cos (3.141592. . .).
- Cosine Function is used to model many real-life cases such as radio waves, tides, musical tones, sound waves, and electric current.
Read More: NCERT Solutions for Class 11 Mathematics Trigonometric Functions
Key Terms: Cos, Cos 180 Degrees, Cosine Function, Hypotenuse, Trigonometric Ratios, Trigonometric Functions, Trigonometry, Sine
What is Cosine?
[Click Here for Sample Questions]
Cosine is a primary trigonometric ratio in Mathematics. Cosine Function is one of the three main primary trigonometric functions along with Sine (sin), and Tangent (tan).
- Cosine is the ratio of the adjacent side to that of the hypotenuse of a right-angled triangle.
- It is denoted as cos x, where x refers to the angle.
- Cos 120°, 150° and 180° have negative values while cos 0°, 30°, etc. have positive values.
- Cosine Graph is an up-down graph that starts from 90 (or π/2).
Read More:
Value of Cos 180 Degrees
[Click Here for Previous Years’ Questions]
Value of Cos 180 Degrees is calculated as -1.
| Value of Cos 180 Degrees = -1 |
Cos 180 Degrees can also be expressed in radians (3.14159 . . .). Cos 180 Degrees can be converted into radians using the degree to radian conversion,
θ in Radians = θ in Degrees × (pi/180°)
180 Degrees = 180° × (π/180°) rad = π or 3.1415 . . .
Thus,
| Cos 180° = Cos (3.1415) = -1 |
Trigonometric Functions Detailed Video Explanation
Derivation of Value of Cos 180 Degrees
[Click Here for Sample Questions]
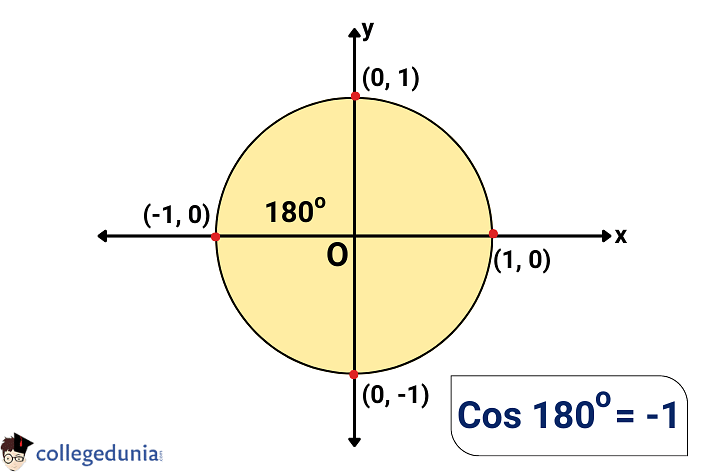
Consider a Unit Circle, which is divided into four quadrants in the Cartesian plane. The value of 180 degrees is in the second quadrant and thus the values of cosine values in the second quadrant are always negative.
- Value of Cos 180 Degrees can also be obtained by subtracting the value of cos 0°.
- The actual value of cos 0 degrees is 1.
- As a result, Cos 180 degree is -(cos 0), which equals - (1)
- Thus, the Value of Cos 180 Degrees degrees is equal to -1.
How to Find Value of Cos 180 Degrees?
[Click Here for Previous Years’ Questions]
Cos 180° is denoted by the number -1. The value of cos 180 degrees can be determined by two main methods namely:
- Using Unit Circle
- Using Trigonometric Functions
Cos 180 Degrees Using Unit Circle
In order to find the value of cos 180 degrees using a unit circle, follow the given steps:
- Rotate a point ‘r' in the anticlockwise direction to produce a 180° angle with the positive x-axis.
- The x-coordinate (-1) of the point of intersection (-1, 0) of the unit circle and r equals Cos 180 degrees.

Value of Cos 180 Degrees Using Unit Circle
Thus, it can be said that
| Cos 180° = x = -1 |
Read More: Trigonometric Functions Important Questions
Cos 180 Degrees Using Trigonometric Functions
According to quotient trigonometric identity, Cos function can be written in terms of the secant function as follows.
Cos θ = 1 / Secθ
If we substitute the value of θ = 180°, then,
| Cos 180° = 1 / Sec 180° |
The value of Sec 180 degree is -1. By substituting,
Cos 180° = 1 / (-1)
Cos 180° = -1
Cos 180 Degrees can also be represented using trigonometric formulas:
- ± √(1-sin2(180°))
- ± 1/√(1 + tan2(180°))
- ± cot 180°/√(1 + cot2(180°))
- ±√(cosec2(180°) - 1)/cosec 180°
- 1/sec 180°
The ultimate value of cos 180° will be negative because 180° is on the negative x-axis.
Check More:
Cosine Table
[Click Here for Sample Questions]
The values of Cos in different angles are listed in the table below:
| Cosine Degrees | Values |
|---|---|
| Cos 0° | 1 |
| Cos 30° | √3/2 |
| Cos 45° | 1/√2 |
| Cos 60° | 1/2 |
| Cos 90° | 0 |
| Cos 120° | -1/2 |
| Cos 150° | -√3/2 |
| Cos 180° | -1 |
| Cos 270° | 0 |
| Cos 360° | 1 |
Trigonometry Table
[Click Here for Previous Years’ Questions]
Trigonometry Table is used to find the values of standard trigonometric angles such as 0°, 30°, 45°, 60° and 90°. The table consists of the values of the different angles of six trigonometric ratios namely sine, cosine, tangent, cosecant, secant, and cotangent.
| Trigonometry Ratios Table | ||||||||
|---|---|---|---|---|---|---|---|---|
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Things to Remember
- Trigonometry is a branch of Mathematics that deals with the relationships between the sides and angles of triangles.
- Cosine (Cos) is one of the primary trigonometric functions along with Sine and Tangent.
- Cosine is the ratio of the adjacent side of a right-angled triangle to its hypotenuse.
- Value of Cos 180 Degrees is equal to -1.
- Its value is negative as it lies in the negative x-axis in the Unit Circle Diagram.
- Value of Cos 180 Degrees can be derived using the Unit Circle and Trigonometric Functions.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Previous Years’ Questions
- ABCD is a trapezium such that AB and CD are parallel… (JEE Main – 2013]
- If the angles of elevation of the top of a tower from three collinear points… (JEE MAIN – 2015)
- Consider a triangular plot ABC with sides AB = 7m, BC=5m… (JEE MAIN – 2019)
- If the sum of all the solutions of the equation… (JEE MAIN – 2018)
- If [x] denotes the greatest integer ≤x, then the system of linear equations x + y = 0x+y=0… (JEE MAIN – 2019)
- Let a vertical tower AB have its end A on the level ground. Let... (JEE MAIN – 2017)
- The number of solutions of 2 sinx + cosx = 3 is… (WBJEE – 2011)
- Let f(?) = (1+sin2?)(2−sin2?). Then for all values of ?… (WBJEE – 2013)
- Let p,q and r be the sides opposite to the angles P,Q and R, respectively… (WBJEE – 2012)
- If 0≤x<π/2, then the number of values of x for which... (JEE MAIN – 2019)
Sample Questions
Ques. What will be the value of 2 cos (180°)/3 sin(-90°)? (3 Marks)
Ans. According to the trigonometric identities,
cos(180°) = sin(90° - 180°)
cos(180°) = sin(-90°)
Now, the given equation is
2 cos(180°) / 3 sin(-90°) = 2 x -1 / 3 x -1 = 2/3
Thus, the value of 2 cos(180°) / 3 sin(-90°) is 2/3.
Ques. Determine the value of (cos² 90° - sin² 90°). [cos 180° = -1] (3 Marks)
Ans. Using the cos 2a formula, we get
(cos² 90° - sin² 90°) = cos(2 × 90°) = cos 180°
Value of Cos 180° = -1, so substituting it, we get
(cos² 90° - sin² 90°) = -1
Thus, the value of (cos² 90° - sin² 90°) is -1.
Ques. What is Cos 180 Degrees? (2 Marks)
Ans. Cosine is a trigonometric ratio of the adjacent side and hypotenuse of a right-angled triangle. Cos 180 Degrees is the value of the cosine trigonometric function for an angle of 180 degrees.
Value of Cos 180 Degrees is -1.
Ques. What will be the value of the length of the base of a right-angled triangle if cos x = 0.8 and the length of the hypotenuse is 5 units? (3 Marks)
Ans. Cosine Function is given as
Cos x = Base/Hypotenuse
Here,
- cos x = 0.8
- Hypotenuse = 5 Units
Therefore, 0.8 = Base/5
Base = 5 × 0.8 = 4
Thus, the length of the base is 4 units.
Ques. What is the value of Cos 180 Degrees in terms of Cot 180°? (2 Marks)
Ans. Using trigonometric identities, the Cosine function can be expressed in terms of the cotangent function.
Cos 180° is represented as -cot 180°/√(1 + cot2(180°)).
Ques. How to Calculate Cos 180 Degrees? (2 Marks)
Ans. Value of Cos 180 Degrees can be computed by building an angle of 180 degrees with the x-axis and then obtaining the coordinates of the corresponding point (-1, 0) on the unit circle. The x-coordinate is equivalent to the value of cos 180°.
Cos 180° = x = -1
Ques. How to find Value of Cos 180 Degrees in terms of other trigonometric functions? (3 Marks)
Ans. The Value of Cos 180° can be expressed in terms of other trigonometric functions using the trigonometry formulas:
- ± √(1-sin2(180°))
- ± 1/√(1 + tan2(180°))
- ± cot 180°/√(1 + cot2(180°))
- ± √(cosec2(180°) - 1)/cosec 180°
- 1/sec 180°
Ques. Solve (1-sin²(180°)) using the Value of Cos 180 Degrees. (1 Mark)
Ans. It is known that
(1-sin²(180°)) = (cos²(180°)) = 1
(1-sin²(180°)) = 1
Ques. If θ = 45°, then What is the value of 2 sec2θ + 3 cosec2θ? (2 Marks)
Ans. 2 sec2θ + 3 cosec2θ = 2 sec2 45° + 3 cosec2 45°
= 2(2–√)2 + 3 (2–√)2
= 4 + 6
= 10
Ques. If cos x = cos 40°. sin 50° + sin 40°. cos 50°, then find the value of x. (2 Marks)
Ans. cos x = cos 40° sin 50° + sin 40° cos 50°
cos x = cos 40° sin(90° – 40°) + sin 40°.cos(90° – 40°)
cos x = cos2 40° + sin² 40°
cos x = 1 …[\(\because\) cos2A + sin2 A = 1
cos x = cos 0°
⇒ x = 0°
Check-Out:





Comments