Question:
The reaction, $A \rightarrow B$ follows first order kinetics. The time taken for $0.8$ mole of A to produce $0.6$ mole of B is 1h. What is the time taken for the conversion of $0.9$, mole of A to $0.675$ mole of $B$?
The reaction, $A \rightarrow B$ follows first order kinetics. The time taken for $0.8$ mole of A to produce $0.6$ mole of B is 1h. What is the time taken for the conversion of $0.9$, mole of A to $0.675$ mole of $B$?
Updated On: Jun 23, 2024
- 0.25 h
- 2 h
- 1 h
- 0.5 h
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Rate constant of first order reaction
$\hspace10mm k=\frac{2.303}{t} \, log_{10} \frac{(A)_0}{(A)_t}$
or $\hspace10mm k=\frac{2.303}{1} \times log_{10} \, \frac{0.8}{0.2} \hspace15mm ...(i)$
(because 0.6 mole of B is formed)
Suppose $t_1$ hour are required for changing the concentration of A from 0.9 mole to 0.675 mole of B.
Remaining mole of $A = 0.9 - 0.675 = 0.225$
$\therefore \hspace10mm k=\frac{2.303}{t_1} \, log_{10} \, \frac{0.9}{0.225} \hspace15mm ...(ii)$
From Eqs. (i) and (ii)
$ \, \, \, \, \, \, \frac{2.303}{1} \, log_{10} \, \frac{0.8}{0.2}=\frac{2.303}{t_1} log_{10} \, \frac{0.9}{0.225}$
$ \, \, \, \, \, \, \, 2.303 \, log_{10} \, 4=\frac{2.303}{t_1} \, log_{10} \, 4$
$\hspace25mm t_1=1 \, h$
$\hspace10mm k=\frac{2.303}{t} \, log_{10} \frac{(A)_0}{(A)_t}$
or $\hspace10mm k=\frac{2.303}{1} \times log_{10} \, \frac{0.8}{0.2} \hspace15mm ...(i)$
(because 0.6 mole of B is formed)
Suppose $t_1$ hour are required for changing the concentration of A from 0.9 mole to 0.675 mole of B.
Remaining mole of $A = 0.9 - 0.675 = 0.225$
$\therefore \hspace10mm k=\frac{2.303}{t_1} \, log_{10} \, \frac{0.9}{0.225} \hspace15mm ...(ii)$
From Eqs. (i) and (ii)
$ \, \, \, \, \, \, \frac{2.303}{1} \, log_{10} \, \frac{0.8}{0.2}=\frac{2.303}{t_1} log_{10} \, \frac{0.9}{0.225}$
$ \, \, \, \, \, \, \, 2.303 \, log_{10} \, 4=\frac{2.303}{t_1} \, log_{10} \, 4$
$\hspace25mm t_1=1 \, h$
Was this answer helpful?
0
0
Top Questions on kinetics equations
- If the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probable, the average, and the root mean square speeds, respectively, is
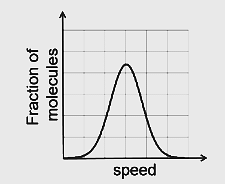
- JEE Advanced - 2020
- Chemistry
- kinetics equations
- The time required to complete 3/4th of first order reaction is 32 min. then find \(t_{\frac{1}{2}}\)
- JIPMER MBBS - 2018
- Chemistry
- kinetics equations
- The half life period of a first order chemical reaction is 6.93 minutes. The time required for the completion of 99% of the chemical reaction will be (log 2 = 0.301)
- VITEEE - 2017
- Chemistry
- kinetics equations
- In a bimolecular reaction, the steric factor $P$ was experimentally determined to be $4.5.$ The correct option(s) among the following is(are)
- JEE Advanced - 2017
- Chemistry
- kinetics equations
- The integrated rate equation is $ kt=\log \,C_{0}-\log C_{t} $ . The straight line graph is obtained by plotting
- Haryana PMT - 2008
- Chemistry
- kinetics equations
View More Questions
Questions Asked in NEET exam
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)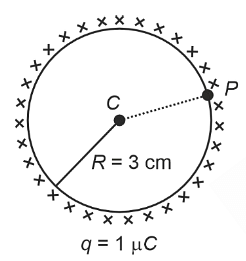
- NEET (UG) - 2024
- Electric Potential And Potential Difference
- A thin flat circular disc of radius 4.5 cm is placed gently over the surface of water. If surface tension of water is 0.07 Nm-1, then the excess force required to take it away from the surface is :
- NEET (UG) - 2024
- Surface tension
- A light ray enters through a right angled prism at point P with the angle of incidence 30° as shown in figure. It travels through the prism parallel to its base BC and emerges along the face AC. The refractive index of the prism is :
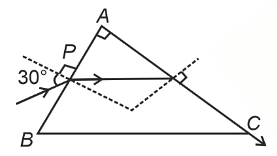
- NEET (UG) - 2024
- Refraction Through A Prism
- Given below are two statements:
Statement I: Both [Co(NH3)6]3+ and [CoF6]3- complexes are octahedral but differ in their magnetic behaviour.
Statement II: [Co(NH3)6]3+ is diamagnetic whereas [CoF6]3- is paramagnetic.
In the light of the above statements, choose the correct answer from the options given below:- NEET (UG) - 2024
- Electronic configuration of atoms and ions
- A thermodynamic system is taken through the cycle abcda. The work done by the gas along the path bc is :
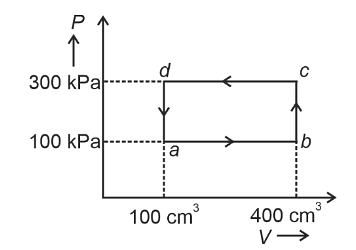
- NEET (UG) - 2024
- Thermodynamics
View More Questions
NEET Notification
 NEET 2024 Paper Analysis Out, Check Subject-wise Difficulty LevelJune 23, 2024
NEET 2024 Paper Analysis Out, Check Subject-wise Difficulty LevelJune 23, 2024NEET 2024 Paper Analysis is now available. Candidates can check the subject-wise difficulty levels here.
Concepts Used:
Kinetics Equations
It is branch of physics that defines motion with respect to space and time is known as kinematics.
Inverse Kinematics: Inverse Kinematics do the reverse of kinematics.
There are four basic kinematics equations:

Rotational Kinematics Equations
Another branch of kinematics equations which deals with the rotational motion of anybody.




